树状数组
树状数组 重点是在树状的数组
大家都知道二叉树吧
叶子结点代表A数组A[1]~A[8]

变形一下
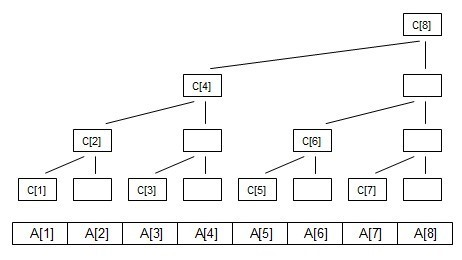
C[i]代表 子树的叶子结点的权值之和// 这里以求和举例
如图可以知道
C[1]=A[1];
C[2]=A[1]+A[2];
C[3]=A[3];
C[4]=A[1]+A[2]+A[3]+A[4];
C[5]=A[5];
C[6]=A[5]+A[6];
C[7]=A[7];
C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8];
将C[]数组的结点序号转化为二进制
1=(001) C[1]=A[1];
2=(010) C[2]=A[1]+A[2];
3=(011) C[3]=A[3];
4=(100) C[4]=A[1]+A[2]+A[3]+A[4];
5=(101) C[5]=A[5];
6=(110) C[6]=A[5]+A[6];
7=(111) C[7]=A[7];
8=(1000) C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8];
1>求A数组中前i项的和
举个例子 i=7;
sum[7]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7] ;
前i项和
C[4]=A[1]+A[2]+A[3]+A[4];
C[6]=A[5]+A[6];
C[7]=A[7];
可以推出: sum[7]=C[4]+C[6]+C[7];
序号写为二进制: sum[(111)]=C[(100)]+C[(110)]+C[(111)];
Code:
int getsum(int i){ //求A[1 - i]的和
int res = 0;
while(i > 0){
res += c[i];
i -= lowbit(i);
}
return res;
}
2>单点更新

如图:
当更新A[1]时 需要向上更新C[1] ,C[2],C[4],C[8]
C[1], C[2], C[4], C[8]
C[(001)], C[(010)], C[(100)], C[(1000)]
1 C[1]+=A[1]
1+lowbit(1)=2(010) C[2]+=A[1]
2+lowbit(2)=4(100) C[4]+=A[1]
4+lowbit(4)=8(1000) C[8]+=A[1]
Code:
void updata(int i,int k){ //在i位置加上k
while(i <= n){
c[i] += k;
i += lowbit(i);
}
}