Sightseeing
Time Limit: 3000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1023 Accepted Submission(s): 444
Problem Description
Tour operator Your Personal Holiday organises guided bus trips across the Benelux. Every day the bus moves from one city S to another city F. On this way, the tourists in the bus can see the sights alongside the route travelled. Moreover, the bus makes a number of stops (zero or more) at some beautiful cities, where the tourists get out to see the local sights.
Different groups of tourists may have different preferences for the sights they want to see, and thus for the route to be taken from S to F. Therefore, Your Personal Holiday wants to offer its clients a choice from many different routes. As hotels have been booked in advance, the starting city S and the final city F, though, are fixed. Two routes from S to F are considered different if there is at least one road from a city A to a city B which is part of one route, but not of the other route.
There is a restriction on the routes that the tourists may choose from. To leave enough time for the sightseeing at the stops (and to avoid using too much fuel), the bus has to take a short route from S to F. It has to be either a route with minimal distance, or a route which is one distance unit longer than the minimal distance. Indeed, by allowing routes that are one distance unit longer, the tourists may have more choice than by restricting them to exactly the minimal routes. This enhances the impression of a personal holiday.
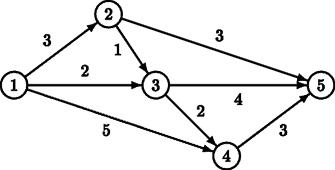
For example, for the above road map, there are two minimal routes from S = 1 to F = 5: 1 → 2 → 5 and 1 → 3 → 5, both of length 6. There is one route that is one distance unit longer: 1 → 3 → 4 → 5, of length 7.
Now, given a (partial) road map of the Benelux and two cities S and F, tour operator Your Personal Holiday likes to know how many different routes it can offer to its clients, under the above restriction on the route length.
Different groups of tourists may have different preferences for the sights they want to see, and thus for the route to be taken from S to F. Therefore, Your Personal Holiday wants to offer its clients a choice from many different routes. As hotels have been booked in advance, the starting city S and the final city F, though, are fixed. Two routes from S to F are considered different if there is at least one road from a city A to a city B which is part of one route, but not of the other route.
There is a restriction on the routes that the tourists may choose from. To leave enough time for the sightseeing at the stops (and to avoid using too much fuel), the bus has to take a short route from S to F. It has to be either a route with minimal distance, or a route which is one distance unit longer than the minimal distance. Indeed, by allowing routes that are one distance unit longer, the tourists may have more choice than by restricting them to exactly the minimal routes. This enhances the impression of a personal holiday.

For example, for the above road map, there are two minimal routes from S = 1 to F = 5: 1 → 2 → 5 and 1 → 3 → 5, both of length 6. There is one route that is one distance unit longer: 1 → 3 → 4 → 5, of length 7.
Now, given a (partial) road map of the Benelux and two cities S and F, tour operator Your Personal Holiday likes to know how many different routes it can offer to its clients, under the above restriction on the route length.
Input
The first line of the input file contains a single number: the number of test cases to follow. Each test case has the following format:
One line with two integers N and M, separated by a single space, with 2 ≤ N ≤ 1,000 and 1 ≤ M ≤ 10, 000: the number of cities and the number of roads in the road map.
M lines, each with three integers A, B and L, separated by single spaces, with 1 ≤ A, B ≤ N, A ≠ B and 1 ≤ L ≤ 1,000, describing a road from city A to city B with length L.
The roads are unidirectional. Hence, if there is a road from A to B, then there is not necessarily also a road from B to A. There may be different roads from a city A to a city B.
One line with two integers S and F, separated by a single space, with 1 ≤ S, F ≤ N and S ≠ F: the starting city and the final city of the route.
There will be at least one route from S to F.
One line with two integers N and M, separated by a single space, with 2 ≤ N ≤ 1,000 and 1 ≤ M ≤ 10, 000: the number of cities and the number of roads in the road map.
M lines, each with three integers A, B and L, separated by single spaces, with 1 ≤ A, B ≤ N, A ≠ B and 1 ≤ L ≤ 1,000, describing a road from city A to city B with length L.
The roads are unidirectional. Hence, if there is a road from A to B, then there is not necessarily also a road from B to A. There may be different roads from a city A to a city B.
One line with two integers S and F, separated by a single space, with 1 ≤ S, F ≤ N and S ≠ F: the starting city and the final city of the route.
There will be at least one route from S to F.
Output
For every test case in the input file, the output should contain a single number, on a single line: the number of routes of minimal length or one distance unit longer. Test cases are such, that this number is at most 10^9 = 1,000,000,000.
Sample Input
2
5 8
1 2 3
1 3 2
1 4 5
2 3 1
2 5 3
3 4 2
3 5 4
4 5 3
1 5
5 6
2 3 1
3 2 1
3 1 10
4 5 2
5 2 7
5 2 7
4 1
Sample Output
3
2
题目链接:HDU 1688
后一题原理一模一样,就不放题面了,题目要分别求最短路和次短路两者的条数与长度,若次短路长度刚好比最短路长1,则答案加上最短路的……
这题简直搞的无语,由于以前只会SPFA模版,并不知道Dij的思路,然而搜到的都是用朴素Dij做的,于是重新看了下离散数学和数据结构的最短路求法——每一次找一个不在S中且离源点最近的点进行拓展,按照这样的顺序得到一系列长度递增(感觉应该是不减的序列)的顺序序列D{i},然后这题怎么套呢。
就分四种情况,比最短路短,跟最短路一样长,比次短路短,跟次短路一样长,第一种情况下要先更新次短再更新最短,然后就是一个比较不复杂的Dij,不过网上的题解都是说循环2*n-1次,但是我觉得是2*n次,因为普通的Dij确实是n-1次因为初始化的时候直接对邻接S起点的点进行了拓展然后让vis[s]=1,但是这题可以不进行拓展只要vis[s]保持0即可,就是让S这个集合初始化为空,起点s的初始化也直接让下面的循环去更新,以前用A*什么的直接爆炸超时……too naive啊,毕竟另外一题范围是10^9,相信数据不会这么友好……
代码:
#include <stdio.h>
#include <bits/stdc++.h>
using namespace std;
#define INF 0x3f3f3f3f
#define CLR(arr,val) memset(arr,val,sizeof(arr))
#define LC(x) (x<<1)
#define RC(x) ((x<<1)+1)
#define MID(x,y) ((x+y)>>1)
typedef pair<int,int> pii;
typedef long long LL;
const double PI=acos(-1.0);
const int N=1010;
const int M=10010;
struct edge
{
int to;
int pre;
int w;
};
edge E[M];
int head[N],tot,n,m;
int d[N][2],way[N][2];
int vis[N][2];
void init()
{
CLR(head,-1);
tot=0;
CLR(d,INF);
CLR(way,0);
CLR(vis,0);
}
inline void add(int s,int t,int w)
{
E[tot].to=t;
E[tot].w=w;
E[tot].pre=head[s];
head[s]=tot++;
}
void Dij(int s)
{
d[s][0]=0;
way[s][0]=1;
for (int i=0; i<2*n; ++i)
{
int cur=-1;
int minm=INF;
int flag=0;
for (int j=1; j<=n; ++j)
{
if(!vis[j][0]&&minm>d[j][0])
{
flag=0;
minm=d[j][0];
cur=j;
}
else if(!vis[j][1]&&minm>d[j][1])
{
flag=1;
minm=d[j][1];
cur=j;
}
}
if(cur==-1)
break;
vis[cur][flag]=1;
for (int j=head[cur]; ~j; j=E[j].pre)
{
int v=E[j].to;
int w=E[j].w;
if(d[v][0]>d[cur][flag]+w)
{
d[v][1]=d[v][0];
way[v][1]=way[v][0];
d[v][0]=d[cur][flag]+w;
way[v][0]=way[cur][flag];
}
else if(d[v][0]==d[cur][flag]+w)
way[v][0]+=way[cur][flag];
else if(d[v][1]>d[cur][flag]+w)
{
d[v][1]=d[cur][flag]+w;
way[v][1]=way[cur][flag];
}
else if(d[v][1]==d[cur][flag]+w)
way[v][1]+=way[cur][flag];
}
}
}
int main(void)
{
int tcase,a,b,w,s,t,i;
scanf("%d",&tcase);
while (tcase--)
{
init();
scanf("%d%d",&n,&m);
for (i=0; i<m; ++i)
{
scanf("%d%d%d",&a,&b,&w);
add(a,b,w);
}
scanf("%d%d",&s,&t);
Dij(s);
int ans=way[t][0];
if(d[t][0]+1==d[t][1])
ans+=way[t][1];
printf("%d
",ans);
}
return 0;
}