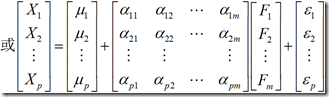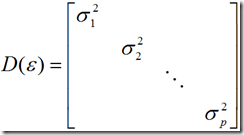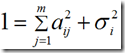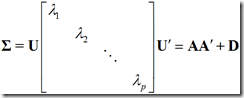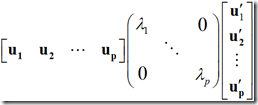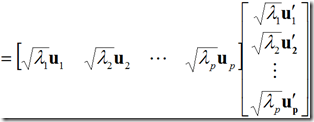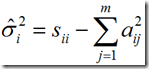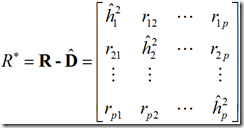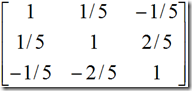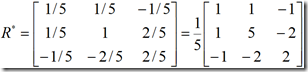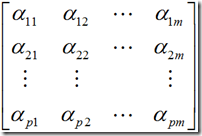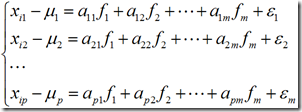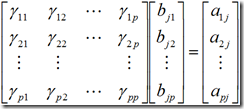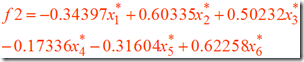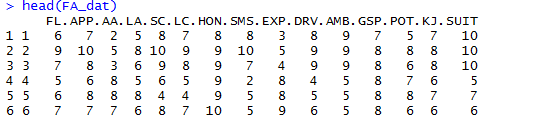题注:主成分分析分析与因子分析也有不同,主成分分析仅仅是变量变换,而因子分析需要构造因子模型。主成分分析:原始变量的线性组合表示新的综合变量,即主成分;因子分析:潜在的假想变量和随机影响变量的线性组合表示原始变量。因子分析与回归分析不同,因子分析中的因子是一个比较抽象的概念,而回归因子有非常明确的实际意义!
一. 问题引入
你是否曾经遇到过以下问题:
二. 概念
| 1. 高中大家都读过吧?(没读过怎么可能看到我这篇文章,真闹心,哈哈!)那是一个以成绩论英雄的时代,理科王子、文科小生是时代标签!对一个学生的数学、物理、化学、语文、历史、英语成绩,如何对其进行正确评价以便进行正确的排名呢?(大家想一想:为什么将数学、物理、化学归理科呢?其他的归为文科?有没有数据支持呢?) 2. 最近股市很牛啊,杀猪大爷与卖菜大妈都入市啦!比如我现在就比较冷静,想通过数据来分析某些股票是否只能买!对于沪深两市证券交易所48家上市公司的13个财务指标数据。13个财务指标分别为:流动比率(X1)、速动比率(X2)、总资产周转率(X3)、存货周转率(X4)、营运资本(X5)、每股收益(X6)、净利润增长率(X7)、每股收益增长率(X8)、主营业务毛利率(X9)、主营业务利润率(X10)、成本费用利润率(X11)、净资产收益率(X12)、总资产利润率(X13)。显然,这13个变量的相关性较强,如果利用因子分析得到低维的新变量来进行我的个股分析呢? 3. 通常我们可以得到关于衡量一个国家经济实力的N多维度数据,显然,如果把这些指标全部用上来进行分析,难免会出现信息重叠,因此,也需要利用FA来进行降维处理! 4. 企业形象或品牌形象的研究中,消费者通过一个有24个指标构成的评价体系,评价百货商场的24个方面的优劣!但消费者主要关心的是三个方面,即商店的环境、商店的服务和商品的价格。因子分析方法可以通过24个变量,找出反映商店环境、商店服务水平和商品价格的三个潜在的因子,对商店进行综合评价 5…………………………………………………………………………………………………………………… |
二. 概念
<R in nutshell>一书的解释:Suppose that you wanted to measure intelligence. It’s not possible to directly measure an abstract concept like intelligence, but it is possible to measure performance on different tests. You could use factor analysis to analyze a set of test scores (the observed values) to try to determine intelligence (the hidden value:因子).
维基百科的解释:Factor analysis is a statistical method used to describe variability among observed, correlated variables in terms of a potentially lower number of unobserved variables called factors. For example, it is possible that variations in four observed variables mainly reflect the variations in two unobserved variables.The observed variables are modelled as linear combinations of the potential factors, plus "error" terms。
百度百科的解释:因子分析的主要目的是用来描述隐藏在一组测量到的变量中的一些更基本的,但又无法直接测量到的隐性变量 (latent variable, latent factor)。最早由英国心理学家C.E.斯皮尔曼提出。他发现学生的各科成绩之间存在着一定的相关性,一科成绩好的学生,往往其他各科成绩也比较好,从而推想是否存在某些潜在的共性因子,或称某些一般智力条件影响着学生的学习成绩。因子分析可在许多变量中找出隐藏的具有代表性的因子。将相同本质的变量归入一个因子,可减少变量的数目,还可检验变量间关系的假设。
一句话因子分析:因子分析(factor analysis)是一种数据简化技术。它通过研究众多变量之间的内部依赖关系,探求观测数据中的基本结构,并用少数几个假想变量来表示其基本的数据结构。这几个假想变量能够反映原来众多变量的主要信息。原始的变量是可观测的显在变量,而假想变量是不可观测的潜在变量,称为因子, 如下:
称![]() 是不可观测的潜在因子。24个变量共享这三个因子,但是每个变量又有自己的个性,不被包含的部分 ,称为特殊因子。
是不可观测的潜在因子。24个变量共享这三个因子,但是每个变量又有自己的个性,不被包含的部分 ,称为特殊因子。
三. 因子分析模型
1. 数据模型
称为![]() 公共因子,是不可观测的变量,他们的系数称为因子载荷。
公共因子,是不可观测的变量,他们的系数称为因子载荷。 ![]() 是特殊因子,是不能被前m个公共因子包含的部分。并且满足:
是特殊因子,是不能被前m个公共因子包含的部分。并且满足:
2. 因子分析模型的性质
1)原始变量X的协方差矩阵的分解
D的主对角线上的元素值越小,则公共因子共享的成分越多。
2)因子载荷不是唯一的
3)模型不受计量单位的影响
3. 因子载荷矩阵中的几个统计特征
1)因子载荷aij的统计意义
因子载荷aij是第i个变量与第j个公共因子的相关系数
根据公共因子的模型性质,有![]() (载荷矩阵中第i行,第j列的元素)反映了第i个变量与第j个公共因子的相关重要性。绝对值越大,相关的密切程度越高。
(载荷矩阵中第i行,第j列的元素)反映了第i个变量与第j个公共因子的相关重要性。绝对值越大,相关的密切程度越高。
2)变量共同度的统计意义
定义:变量![]() 的共同度是因子载荷矩阵的第i行的元素的平方和。记为
的共同度是因子载荷矩阵的第i行的元素的平方和。记为![]()
统计意义:
所有的公共因子和特殊因子对变量![]() 的贡献为1。如果
的贡献为1。如果![]() 非常靠近1,
非常靠近1,![]() 非常小,则因子分析的效果好,从原变量空间到公共因子空间的转化性质好。
非常小,则因子分析的效果好,从原变量空间到公共因子空间的转化性质好。
3)公共因子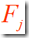 方差贡献的统计意义
方差贡献的统计意义
因子载荷矩阵中各列元素的平方和
称为第j个公共因子![]() 对所有分量
对所有分量![]()
![]() 的方差贡献和。衡量
的方差贡献和。衡量![]() 的相对重要性。
的相对重要性。
4. 因子载荷矩阵的估计方法
1)主分分分析法
设随机向量 ![]() 的均值为
的均值为![]() ,协方差为
,协方差为![]() ,
,![]() 为
为![]() 的特征根,
的特征根,![]() 为对应的标准化特征向量,则
为对应的标准化特征向量,则
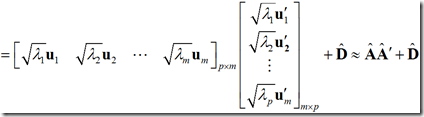
上式给出的![]() 表达式是精确的,然而,它实际上是毫无价值的,因为我们的目的是寻求用少数几个公共因子解释,故略去后面的p-m项的贡献,有
表达式是精确的,然而,它实际上是毫无价值的,因为我们的目的是寻求用少数几个公共因子解释,故略去后面的p-m项的贡献,有
上式有一个假定,模型中的特殊因子是不重要的,因而从S的分解中忽略了特殊因子的方差。
2)主因子法
主因子方法是对主成分方法的修正,假定我们首先对变量进行标准化变换。则
R=AA’+D
R*=AA’=R-D
称R*为约相关矩阵,R*对角线上的元素是![]() ,而不是1。设
,而不是1。设![]() 是
是![]() 的初始估计,则
的初始估计,则![]()
3)极大似然估计法
如果假定公共因子F和特殊因子![]() 服从正态分布,那么可以得到因子载荷和特殊因子方差的极大似然估计。设
服从正态分布,那么可以得到因子载荷和特殊因子方差的极大似然估计。设 ![]() 为来自正态总体
为来自正态总体![]() 的随机样本。
的随机样本。
它通过![]() 依赖A和
依赖A和![]() 。上式并不能唯一确定A,为此可添加一个唯一性条件:
。上式并不能唯一确定A,为此可添加一个唯一性条件:
这里![]() 是一个对角矩阵,用数值极大化的方法可以得到极大似然估计
是一个对角矩阵,用数值极大化的方法可以得到极大似然估计![]() 。极大似然估计
。极大似然估计![]() 将使
将使![]() 为对角阵,且似然函数达到最大。
为对角阵,且似然函数达到最大。
相应的共同度的似然估计为:
第j个因子对总方差的贡献:
4)例子
假定某地固定资产投资率![]() ,通货膨胀率
,通货膨胀率![]() ,失业率
,失业率![]() ,相关系数矩阵为
,相关系数矩阵为
方法一:试用主成分分析法求因子分析模型。
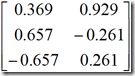
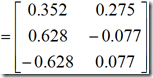
| 手算过程 特征根为:  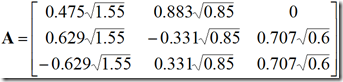  可取前两个因子F1和F2为公共因子,第一公因子F1物价就业因子,对X的贡献为1.55。第一公因子F2为投资因子,对X的贡献为0.85。共同度分别为1,0.706,0.706。 R语言实现 > for(i in 1:3){for(j in 1:i){R[i,j]<-Ltm[(i-1)*i/2+j];R[j,i]<-R[i,j]}}
> R
x1 x2 x3
x1 1.0 0.2 -0.2
x2 0.2 1.0 -0.4
x3 -0.2 -0.4 1.0
> summary(pca)
Importance of components:
Comp.1 Comp.2 Comp.3
Standard deviation 1.2435474 0.9238993 0.7745967
Proportion of Variance 0.5154701 0.2845299 0.2000000
Cumulative Proportion 0.5154701 0.8000000 1.0000000
> pca$loadings
Loadings:
Comp.1 Comp.2 Comp.3
x1 -0.460 0.888
主成分系数矩阵
x2 -0.628 -0.325 0.707
x3 0.628 0.325 0.707
Comp.1 Comp.2 Comp.3
SS loadings 1.000 1.000 1.000
Proportion Var 0.333 0.333 0.333
Cumulative Var 0.333 0.667 1.000
> solve(load) #求load载荷矩阵的逆!(这样直接求逆的计算显示是不对的,行不通!)
x1 x2 x3
Comp.1 -4.597008e-01 -0.6279630 0.6279630
Comp.2 8.880738e-01 -0.3250576 0.3250576
Comp.3 -3.834485e-16 0.7071068 0.7071068
|
方法二:试用主因子分析法求因子分析模型
特征根为:
对应的非零特征向量为:
5. 因子得分
1)因子得分的概念
前面我们主要解决了用公共因子的线性组合来表示一组观测变量的有关问题。如果我们要使用这些因子做其他的研究,比如把得到的因子作为自变量来做回归分析,对样本进行分类或评价,这就需要我们对公共因子进行测度,即给出公共因子的值。
因子分析的数学模型为:
原变量被表示为公共因子的线性组合,当载荷矩阵旋转之后,公共因子可以做出解释,通常的情况下,我们还想反过来把公共因子表示为原变量的线性组合。
可见,要求得每个因子的得分,必须求得分函数的系数,而由于p>m,所以不能得到精确的得分,只能通过估计。
2)因子得分的估计
1、巴特莱特因子得分(加权最小二乘法)
###巴特莱特因子得分计算方法的思想
看成自变量的观测;把某个个案的得分![]() 看成最小二乘法需要求的系数 。
看成最小二乘法需要求的系数 。
由于特殊因子的方差相异,所以用加权最小二乘法求得分,每个各案作一次,要求出所有样品的得分,需要作n次。
3)回归方法
###思想
则,我们有如下的方程组:
j=1,2,…,m
六. 因子分析的步骤、展望和建议
一)因子分析通常包括以下五个步骤
1、选择分析的变量
用定性分析和定量分析的方法选择变量,因子分析的前提条件是观测变量间有较强的相关性,因为如果变量之间
无相关性或相关性较小的话,他们不会有共享因子,所以原始变量间应该有较强的相关性。
2、计算所选原始变量的相关系数矩阵
相关系数矩阵描述了原始变量之间的相关关系。可以帮助判断原始变量之间是否存在相关关系,这对因子分析
是非常重要的,因为如果所选变量之间无关系,做因子分析是不恰当的。并且相关系数矩阵是估计因子结构的基础。
3、提取公共因子
这一步要确定因子求解的方法和因子的个数。需要根据研究者的设计方案或有关的经验或知识事先确定。因子个数的确定可以根据因子方差的大小。只取方差大于1(或特征值大于1)的那些因子,因为方差小于1的因子其贡献可能很小;按照因子的累计方差贡献率来确定,一般认为要达到60%才能符合要求;
4、因子旋转
通过坐标变换使每个原始变量在尽可能少的因子之间有密切的关系,这样因子解的实际意义更容易解释,并为每个潜在因子赋予有实际意义的名字。
5、计算因子得分
求出各样本的因子得分,有了因子得分值,则可以在许多分析中使用这些因子,例如以因子的得分做变量的聚类分析,做回归分析中的回归因子。
因子分析是十分主观的,在许多出版的资料中,因子分析模型都用少数可阐述因子提供了合理解释。实际上,绝大多数因子分析并没有产生如此明确的结果。不幸的是,评价因子分析质量的法则尚未很好量化,质量问题只好依赖一个“哇!”准则。如果在仔细检查因子分析的时候,研究人员能够喊出“哇,我明白这些因子”的时候,就可看着是成功运用了因子分析方法。
七. 直观的例子:国民生活质量的因素分析
国家发展的最终目标,是为了全面提高全体国民的生活质量,满足广大国民日益增长的物质和文化的合理需求。在可持续发展消费的统一理念下,增加社会财富,创自更多的物质文明和精神文明,保持人类的健康延续和生生不息,在人类与自然协同进化的基础上,维系人类与自然的平衡,达到完整的代际公平和区际公平(即时间过程的最大合理性与空间分布的最大合理化)。
从1990年开始,联合国开发计划署(UYNP)首次采用“人文发展系数”指标对于国民生活质量进行测度。人文发展系数利用三类内涵丰富的指标组合,即人的健康状况(使用出生时的人均预期寿命表达)、人的智力程度(使用组合的教育成就表达)、人的福利水平(使用人均国民收入或人均GDP表达),并且特别强调三类指标组合的整体表达内涵,去衡量一个国家或地区的社会发展总体状况以及国民生活质量的总水平。
###在这个指标体系中有如下的指标:
X1——预期寿命;X2——成人识字率;X3——综合入学率;X4——人均GDP(美圆);X5——预期寿命指数;X6——教育成就指数;X7——人均GDP指数;
###旋转后的因子结构
Rotated Factor Pattern
FACTOR1 FACTOR2 FACTOR3
X1 0.38129 0.41765 0.81714
X2 0.12166 0.84828 0.45981
X3 0.64803 0.61822 0.22398
X4 0.90410 0.20531 0.34100
X5 0.38854 0.43295 0.80848
X6 0.28207 0.85325 0.43289
X7 0.90091 0.20612 0.35052
FACTOR1为经济发展因子;FACTOR2为教育成就因子;FACTOR3为健康水平因子
### 被每个因子解释的方差和共同度
Variance explained by each factor
FACTOR1 FACTOR2 FACTOR3
2.439700 2.276317 2.009490
Final Communality Estimates: Total = 6.725507
X1 X2 X3 X4 X5 X6 X7
0.987530 0.945796 0.852306 0.975830 0.992050 0.994995 0.976999
### Standardized Scoring Coefficients标准化得分系数
FACTOR1 FACTOR2 FACTOR3
X1 -0.18875 -0.34397 0.85077
X2 -0.24109 0.60335 -0.10234
X3 0.35462 0.50232 -0.59895
X4 0.53990 -0.17336 -0.10355
X5 -0.17918 -0.31604 0.81490
X6 -0.09230 0.62258 -0.24876
八. R因子实战
1)一个例子搞懂因子分析!
假设有n个学生p个科目的成绩,用X1,X2,……,Xp表示p个科目,Xi=(xi1,xi2,……,xip)其中i=1,2,3……n。表示第i个学生的p科目的成绩,现要分析主要由哪些因素决定学生的学习能力。 科目X所有的因子有m个,如数学推导因子,记忆因子,计算因子等,分别记为f1,f2,……,fm,即 Xi=ai1*f1+ai2*f2+……+aim*fm+@,i=1,2,……,p 用这m个不可观测的互不相关的公共因子f1,f2,……,fm(也称为潜因子)和一个特殊因子@来描述原始可测的相关变量(科目)X1,X2,……,Xp。并解释分析学生的学习能力,他们的系数ai1,ai2,……,aip称为因子载荷,表示第i个科目在m个方面的表现。 以上就是构建的因子模型。
综上:因子分析主要应用于两个方面: ①寻求基本结构,简化观测系统,将具有错综复杂关系的对象(变量或样本)综合为少数几个因子(不可观测的随机变量),以再现因子与原始变量之间的内在联系; ②用于分类,对于p个变量或n个样本进行分类; 因子分析根据研究对象的不同可以分为R型和Q型因子分析。 R型因子分析研究 变量(指标) 之间的相关关系,通过对变量的相关矩阵或协方差矩阵内部结构的研究,找出控制所有变量的几个公共因子(或称为主因子,潜在因子)用以对变量或样本进行分类。 Q型因子分析研究 样本 之间的相关关系,通过对样本的相似矩阵内部结构的研究找出控制样本的几个主要因素(或称为主因子)。 这两种因子分析的处理方法是一样的,只是出发点不同,R型从变量的相关阵出发,Q型从样本的相似矩阵出发.
2)因子分析的计算函数
在R软件中,提供了做因子分析计算的函数-factanal()函数,它可以从样本数据,样本的方差矩阵和相关矩阵出发对数据做因子分析,并可直接给出方差最大的载荷因子矩阵。
|
factanal(x, factors, data = NULL, covmat = NULL, n.obs = NA, subset, na.action, start = NULL, scores = c("none", "regression", "Bartlett"), rotation = "varimax", control = NULL, ...) 参数介绍: x:数据的公式,或者是由数据(每个样本按照行输入)构成矩阵,或者是数据框 factors:因子的个数 data:数据框,当x由公式给出时使用 covmat:样本的协方差矩阵或样本的相关矩阵,此时不必输入变量x scores:因子defender方法,scores="regression",表示用回归方法计算因子得分;当scores="Bartlett"时,表示用Bartlett方法计算因子得分;缺省值为"none"时,即不计算因子得分。 rotation:表示旋转,缺省值为方差最大旋转,当rotation="none"时,不作旋转变换。 |
3)实例
48名应聘者应聘某公司的某职位,公司为这些应聘者的15项指标打分,其指标与得分情况见data数据框,试用因子分析的方法对15想指标做因子分析,在因子分析中选择5个因子。 15项指标说明: 求职信形式:FL
外貌:APP 专业能力:AA 讨人喜欢:LA 自信心:SC 洞察力:LC 诚实:HON 推销能力:SMS 经验:EXP 驾驭水平:DRV 事业心:AMB 理解能力:GSP 潜在能力:POT 交际能力:KJ 适应性:SUIT
|
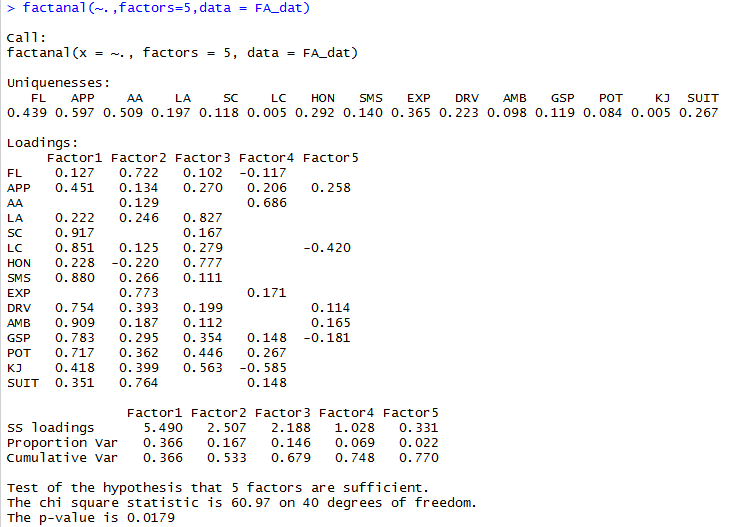
> FA_dat<-read.table('C:/Users/wb-tangyang.b/Desktop/FA_dat.txt',header = TRUE) > factanal(~.,factors=5,data = FA_dat)
|
在得到的结果中,公共因子还有比较鲜明的实际意义:
第一公共因子中,系数绝对值大的变量主要是: 自信心,洞察力,推销能力,驾驭水平,事业心,理解能力,潜在能力,这些主要表现求职者外漏能力
第二公共因子中,系数绝对值大的变量主要是:求职信的形式,经验,适应性,这些主要反映了求职者的经验
第三公共因子中,系数绝对值大的变量主要是:讨人喜欢,诚实,这些主要反映了求职者是否讨人喜欢
第四、第五公共因子系数绝对值较小,这说明这两个公共因子相对次要一些。
第四公共因子中,系数绝对值大的变量主要是:专业能力,交际能力,这些主要反映了求职者的专业能力
第五公共因子中,系数绝对值较大的变量主要是:外貌,洞察力,这些主要反映了求职者的外貌。
通过以上分析,我们得到公共因子和因子载荷,就应当反过来考察每一个样本,如上例,在得到五个公共因子后,应当考察48名应聘者在5个因子得分情况,这样就可以为公司挑选合适本公司的人员。
有两种估计因子得分的方法,加权最小二乘发,回归方法
R软件中,作因子分析的函数factanal()同时给出了这两种方法,当scores="regression"时,采用回归法,当参数为scores="Bartlett"时,采用的是加权最小二乘法。但是,到目前为止,计算因子得分的两种估计方法到底哪一个好还没有结论。
在上例中,计算48名应聘者的因子得分:
> fa<-factanal(~.,factors=5,data=FA_dat,scores="regression")
> fa$scores
Factor1 Factor2 Factor3 Factor4 Factor5
1 0.800717544 0.18668478 -0.851460896 -1.02805665 0.52205818
2 1.116241580 0.47700243 0.001629454 -0.43629124 0.36113830
3 0.879369406 0.29478854 -0.314716179 -1.02965924 0.33082062
4 -0.523388290 0.43753019 0.560799973 0.25097714 0.40522224
5 -0.846808386 1.21550502 1.085816718 0.45502930 1.07029291
6 0.003185837 0.27885951 0.243258421 0.12109434 -0.27226717
7 0.703922279 1.33861950 0.111053822 0.01088589 0.64206809
8 0.896108099 1.37342978 0.232713178 -0.35982102 0.35349535
9 0.455395763 1.17038462 0.244111085 -0.19242716 0.17911705
10 1.843009744 -0.18285199 -1.451198021 1.43700462 0.02806712
11 1.781056933 -0.22818096 -2.089052424 1.48488398 0.95136053
12 1.403740004 -0.53727939 -0.605003245 1.66579885 -0.39726150
13 -0.838419356 0.45881416 1.103624446 0.56651271 0.93295036
14 -0.765006924 0.30471946 0.836846379 0.95059097 1.57972186
15 -0.948618470 0.14818660 0.761841309 1.18822261 0.41131508
16 0.670346434 0.62562847 -0.275204781 0.28878032 -0.58926497
17 0.308422895 0.41267618 -0.135936211 -0.42814543 1.56803728
18 0.295571360 -0.46281204 -0.728936475 -1.16500937 -1.31962760
19 0.184298026 -0.21956636 -0.825069511 -0.55179100 -1.51372977
20 0.372855990 0.03579921 1.021768751 -0.31575185 -0.57686133
21 0.402538565 -0.46066903 0.589465103 0.86890942 -0.14399060
22 0.927698958 0.60250660 0.673815357 -1.14036612 -0.33194886
23 0.931887149 0.47998903 0.990087831 -0.83545711 0.59726767
24 0.585842905 0.66244517 1.202381977 -0.86524797 -0.62640797
25 -0.798685118 -0.23749354 0.480395810 0.05836780 -0.34004466
26 -0.781584615 0.15450648 0.518109233 0.43972335 0.54299850
27 0.372094679 -1.12074511 0.595496294 0.95822481 -1.09577912
28 -0.948459790 -0.81527906 -0.922269220 -1.77326821 -0.35738899
29 -1.213604298 -0.13087983 -1.503827903 -1.92660112 1.10293874
30 -0.484101748 -1.21181187 0.367311077 -1.68214807 0.52310776
31 -0.397976947 -0.69999678 0.622508916 -1.63410675 1.01452372
32 -0.173713063 -1.10108335 0.608407659 -0.12745790 -2.26318679
33 -0.256281136 -1.33038515 0.560781422 -0.40338235 -2.53222879
34 -1.183167544 -0.49422381 -0.008024526 -0.81458656 -0.10274921
35 -1.665000629 -0.33809240 0.059885560 -0.88500404 1.19916519
36 -0.514907574 -0.19120917 0.370984444 -0.45888647 -0.61709089
37 1.321163395 -1.72531922 -1.052264142 0.39130820 0.21100177
38 1.237411113 -1.32542774 -0.635392434 -0.30674409 -0.33706339
39 0.687041364 1.55535677 0.960484537 -0.39006072 -0.30682688
40 0.923821287 1.49189358 0.792049416 -0.40120250 0.04739454
41 -1.740662685 1.55241481 -2.301529543 1.10997918 -0.54355251
42 -1.946665869 1.74562267 -2.660094728 0.70599496 -1.13003023
43 -1.601371579 0.70912444 -0.096524877 0.77685896 -1.29579679
44 0.960832458 0.10579350 -0.315491319 0.20738885 0.51793979
45 -0.309142913 -0.38559454 1.071709950 1.49287914 -0.45272845
46 0.155406236 -0.52531271 1.194207841 1.80067575 -0.93031173
47 -1.182605366 -2.06429652 -0.395197469 1.05832124 1.50773379
48 -1.099807701 -2.02977096 -0.694352061 0.86306058 1.47640173
> plot(fa$scores[,1:2],col='blue')
> text(fa$scores[,1],fa$scores[,2],col = 'red',cex = 0.9,adj = c(0.1,0.1) )
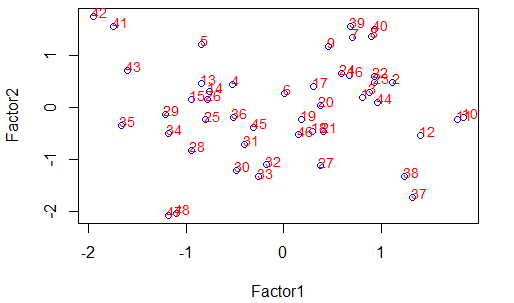
用以上两个语句绘制关于因子1,2的散点图 由前面的分析知,第一因子主要是求职者的外露能力,第二公共因子主要表现求职者的经验,公司可以选择两者得分都比较高的应聘者,若偏重外露能力,则选择第一公共因子得分较大的应聘者,如偏重经验,则可以考虑第二公共因子得分较大的应聘者!
九. 参考文献
http://www.datasoldier.net/post/40.html
http://wenku.baidu.com/view/4904e121192e45361066f522.html
http://wenku.baidu.com/link?url=EwayX82S9pd1TO486JW4iEK2YEjTB-FuNiDlKeVRJ_bEJ4UfubCXbfsCErAw0ZTzfWVtFQvBCXr_7x1CclrYxRtPnVlrwFzyMqE_R9Q8dVW
http://wenku.baidu.com/view/67fb7a5a3b3567ec102d8abd.html
十. 其他补充
(1)对因子分析非常有用的软件包,FactoMineR包不仅提供了PCA和EFA方法,还包含潜变量模型。FAiR包使用遗传算法来估计因子分析模型,增强了模型参数估计能力,能够处理不等式的约束条件;GPArotation包提供了许多因子旋转方法;nFactors包,提供了用来判断因子数目方法。
(2)其他潜变量模型
先验知识的模型:先从一些先验知识开始,比如变量背后有几个因子、变量在因子上的载荷是怎样的、因子间的相关性如何,然后通过收集数据检验这些先验知识。这种方法称作验证性因子分析(CFA);做CFA的软件包:sem、openMx和lavaan等;ltm包可以用来拟合测验和问卷中各项目的潜变量模型。
潜类别模型(潜在的因子被认为是类别型而非连续型)可通过FlexMix、lcmm、randomLCA和poLC包进行拟合。lcda包可做潜类别判别分析,而lsa可做潜在语义分析----一种自然语言处理中的方法。ca包提供了可做简单和多重对应分析的函数。
R中还包含了众多的多维标度法(MDS)计算工具。MDS即可用发现解释相似性和可测对象间距离的潜在维度。cmdscale()函数可做经典的MDS;MASS包中的isoMDS()函数可做非线性MDS;vagan包中则包含了两种MDS的函数