Description
牛牛是一个热爱算法设计的高中生。在他设计的算法中,常常会使用带小数的数进行计算。牛牛认为,如果在 k
进制下,一个数的小数部分是纯循环的,那么它就是美的。现在,牛牛想知道:对于已知的十进制数 n 和 m,在
kk 进制下,有多少个数值上互不相等的纯循环小数,可以用分数 xy 表示,其中 1≤x≤n,1≤y≤m,且 x,y是整数
。一个数是纯循环的,当且仅当其可以写成以下形式:a.c1˙c2c3…cp-1cp˙其中,a 是一个整数,p≥1;对于 1
≤i≤p,ci是 kk 进制下的一位数字。例如,在十进制下,0.45454545……=0.4˙5˙是纯循环的,它可以用 5/11
、10/22 等分数表示;在十进制下,0.1666666……=0.16˙则不是纯循环的,它可以用 1/6 等分数表示。需要特
别注意的是,我们认为一个整数是纯循环的,因为它的小数部分可以表示成 0 的循环或是 k?1 的循环;而一个小
数部分非 0 的有限小数不是纯循环的。
Input
只有一行,包含三个十进制数N,M,K意义如题所述,保证 1≤n≤10^9,1≤m≤10^9,2≤k≤2000
Output
一行一个整数,表示满足条件的美的数的个数。
Sample Input
2 6 10
Sample Output
4
explanation
满足条件的数分别是:
1/1=1.0000……
1/3=0.3333……
2/1=2.0000……
2/3=0.6666……
1/1 和 2/2 虽然都是纯循环小数,但因为它们相等,因此只计数一次;同样,1/3 和 2/6 也只计数一次。
explanation
满足条件的数分别是:
1/1=1.0000……
1/3=0.3333……
2/1=2.0000……
2/3=0.6666……
1/1 和 2/2 虽然都是纯循环小数,但因为它们相等,因此只计数一次;同样,1/3 和 2/6 也只计数一次。
杜教筛板子题
柿子还是比较好推
这里补一个我一直没搞懂的证明
求证:k进制下的纯循环小数的最简分数的分母一定与k互质
设循环节长度为t,最简分数为a/b
所以
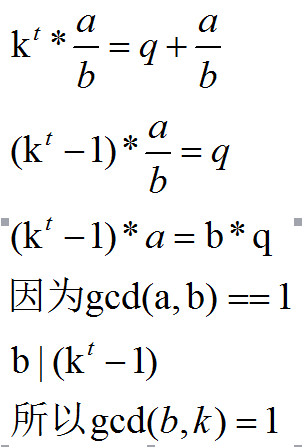

// luogu-judger-enable-o2 //%std #include<iostream> #include<cstdio> #include<cstdlib> #include<cstring> #include<string> #include<algorithm> #include<cmath> #include<vector> #include<queue> #include<stack> #include<set> #include<map> using namespace std; #define lovelive long long #define lc son[x][0] #define rc son[x][1] #define lowbit(x) (x&(-x)) #define pt vc const lovelive mod=19260817; const int N=2e6+100; void read(lovelive &x) { lovelive p=1; x=0; char c=getchar(); while(c<'0'||c>'9') { if(c=='-') p=-1; c=getchar(); } while(c>='0'&&c<='9') { x=x*10+c-48; c=getchar(); } x*=p; } struct hash_map{ int ans[1000010],nxt[1000010],fir[mod+1],tot; lovelive hash[1000010]; void add(lovelive x,int y) { int i=x%mod; nxt[++tot]=fir[i]; fir[i]=tot; ans[tot]=y; hash[tot]=x; } int query(lovelive x) { for(int j=fir[x%mod];j;j=nxt[j]) if(hash[j]==x) return ans[j]; return -1; } }sp; int prime[N],miu[N],pre[N],tot; bool not_prime[N]; void find_prime(int n) { miu[1]=1; for(int i=2;i<=n;i++) { if(!not_prime[i]) prime[++tot]=i,miu[i]=-1,pre[i]=i; for(int j=1;j<=tot&&prime[j]*i<=n;j++) { not_prime[i*prime[j]]=true; pre[i*prime[j]]=prime[j]; if(i%prime[j]==0) break; miu[i*prime[j]]=-miu[i]; } } for(int i=1;i<=n;i++) miu[i]+=miu[i-1]; } lovelive calc(lovelive n) { if(n<=2e6) return miu[n]; int tmp=sp.query(n*2000+1); if(tmp!=-1) return tmp; lovelive ans=1; for(lovelive i=2,r;i<=n;i=r+1) { r=n/(n/i); if(r>n) r=n; ans-=(r-i+1)*calc(n/i); } sp.add(n*2000+1,ans); return ans; } int a[20],cnt; lovelive f[2020]; lovelive calc2(int n,int k) { return (n/k)*f[k]+f[n%k]; } lovelive calc3(lovelive n,int k) { if(n<=1) return n; if(k==1) return calc(n); int tmp=sp.query(n*2000+k); if(tmp!=-1) return tmp; int p=pre[k]; lovelive ans=calc3(n/p,k); tmp=k; while(tmp%p==0) tmp/=p; ans+=calc3(n,tmp); sp.add(n*2000+k,ans); return ans; } int gcd(int x,int y) { if(!y) return x; return gcd(y,x%y); } int main() { lovelive n,m,k; read(n);read(m);read(k); for(int i=1;i<=k;i++) f[i]=(gcd(i,k)==1); for(int i=1;i<=k;i++) f[i]+=f[i-1]; find_prime(2000000); a[0]=1; for(int j=1;prime[j]<=k;j++) if(k%prime[j]==0) { a[1<<cnt]=prime[j]; ++cnt; } for(int j=1;j<(1<<cnt);j++) a[j]=a[j^lowbit(j)]*a[lowbit(j)]; lovelive ans=0; for(lovelive i=1,r;i<=min(n,m);i=r+1) { r=min(n/(n/i),m/(m/i)); if(r>min(n,m)) r=min(n,m); ans+=(calc3(r,k)-calc3(i-1,k))*(n/i)*calc2(m/i,k); } cout<<ans<<" "; return 0; } /* 1000000000 1000000000 960 */
