二叉树 104,111, 226, 100

二叉树具有天然的递归结构。

1. 前序遍历

void preorder(TreeNode* node){
    if(node){
        cout<< node->val;
        preorder(node->left);
        preorder(node->right);
    }
}

或这样写：

void preorder(TreeNode* node){
　　//递归终止条件
    if( node==NULL )
        return;
　　//递归过程
    cout<< node->val;
    preorder(node->left);
    preorder(node->right);

}    

空是一颗二叉树。

2. 查找某个键值key

bool contain(Node* node, Key key){
    //终止条件
    if(node == NULL)
        return false;
    if(key==node->key)
        return true;
    if(contain(node->left, key) || contain(node->right, key))
        return true;
    return false;
}

3. 删除二叉树

void destroy(Node* node){
    if(node == NULL)
        return;
    destroy(node->left);
    destroy(node->right);
    delete node;
    count--;
}

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int maxDepth(TreeNode* root) {
        //递归终止条件
        if(root == NULL)
            return 0;
        
        //当前结点左子树最高的高度
        int leftMaxDepth = maxDepth(root->left);
        int rightMaxDepth = maxDepth(root->right);
        return max(leftMaxDepth, rightMaxDepth)+1;

　　　　/*也可直接写为
　　　　return max(maxDepth(root->left), maxDepth(root->right))+1;
　　　　*/
    }
};

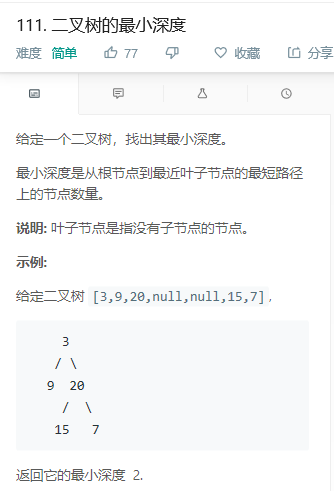
思路：DFS+递归

1）若当前结点若为空，则返回0；

2）若当前结点的左子树为空，则对右子树调用递归函数，并加1返回；

3）若当前结点的右子树为空，则对左子树调用递归函数，并加1返回；

4）若当前结点的左右子树都不为空，则对他们分别调用递归函数，并将二者的较小值加1返回。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int minDepth(TreeNode* root) {
        if(root==NULL) return 0;
        
        if(root->left && root->right)
            return min(minDepth(root->right), minDepth(root->left))+1;
        else
            return max(minDepth(root->right), minDepth(root->left))+1;
    }
};

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int minDepth(TreeNode* root) {
        if(root == NULL) return 0;
        if(root->left == NULL)
            return minDepth(root->right)+1;
        if(root->right == NULL)
            return minDepth(root->left)+1;
        return min(minDepth(root->left), minDepth(root->right))+1;
    }
};

 

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if(root == NULL)
            return NULL;
        invertTree(root->left);
        invertTree(root->right);
        swap(root->left, root->right);
        
        return root;
    }
};

 

/**
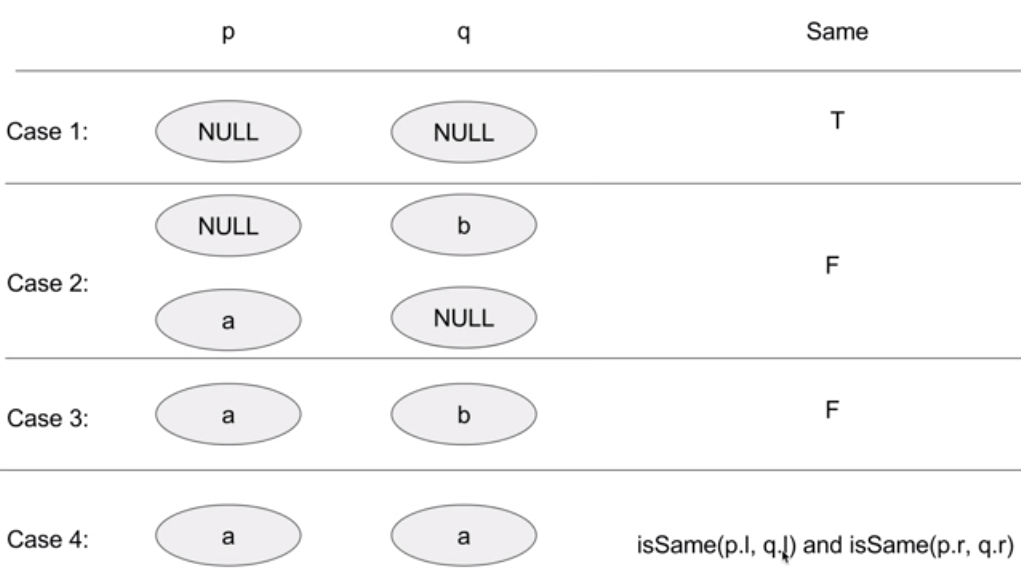
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool isSameTree(TreeNode* p, TreeNode* q) {
        if(!p && !q)
            return true;
        else if(!p && q)
            return false;
        else if(p && !q)
            return false;
        else{
            if(p->val != q->val)
                return false;
            else
                return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
        }
    }
};

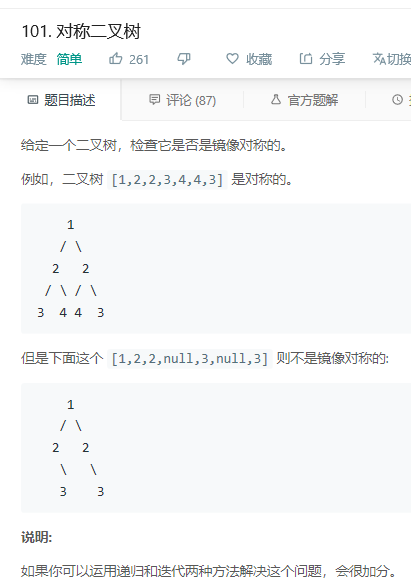
思路：判断二叉树是否是镜面对称的，比如有两个节点n1, n2，我们需要比较n1的左子节点的值和n2的右子节点的值是否相等，同时还要比较n1的右子节点的值和n2的左子结点的值是否相等，以此类推比较完所有的左右两个节点。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        if(!root)
            return true;
        return symmetric(root->left, root->right);
    }
     bool symmetric(TreeNode* left, TreeNode* right){
         if(!left && !right) return true;
         if(left && !right || !left && right || left->val != right->val)
             return false;
         return symmetric(left->left, right->right) && symmetric(left->right, right->left);
         
     }
};