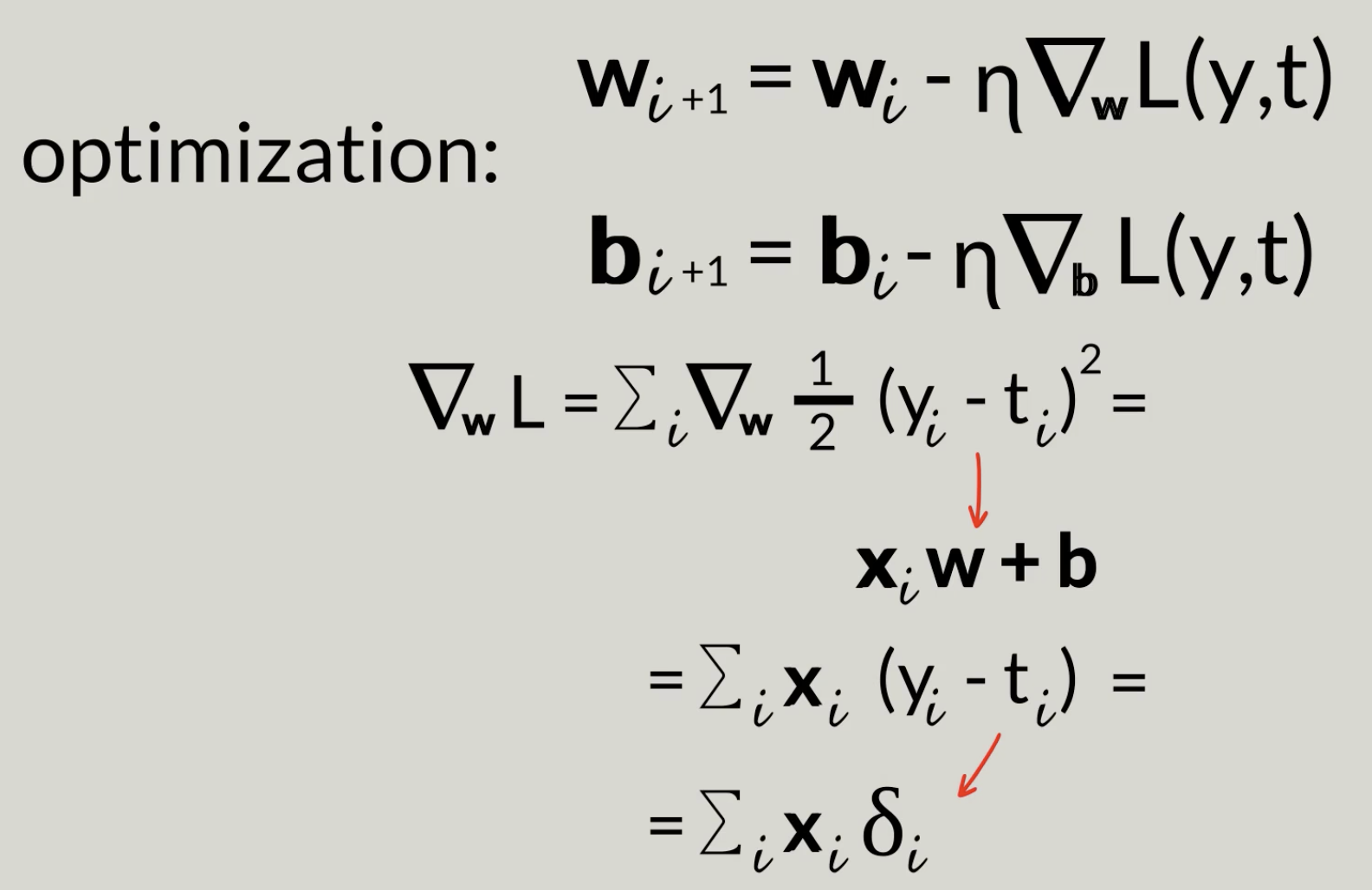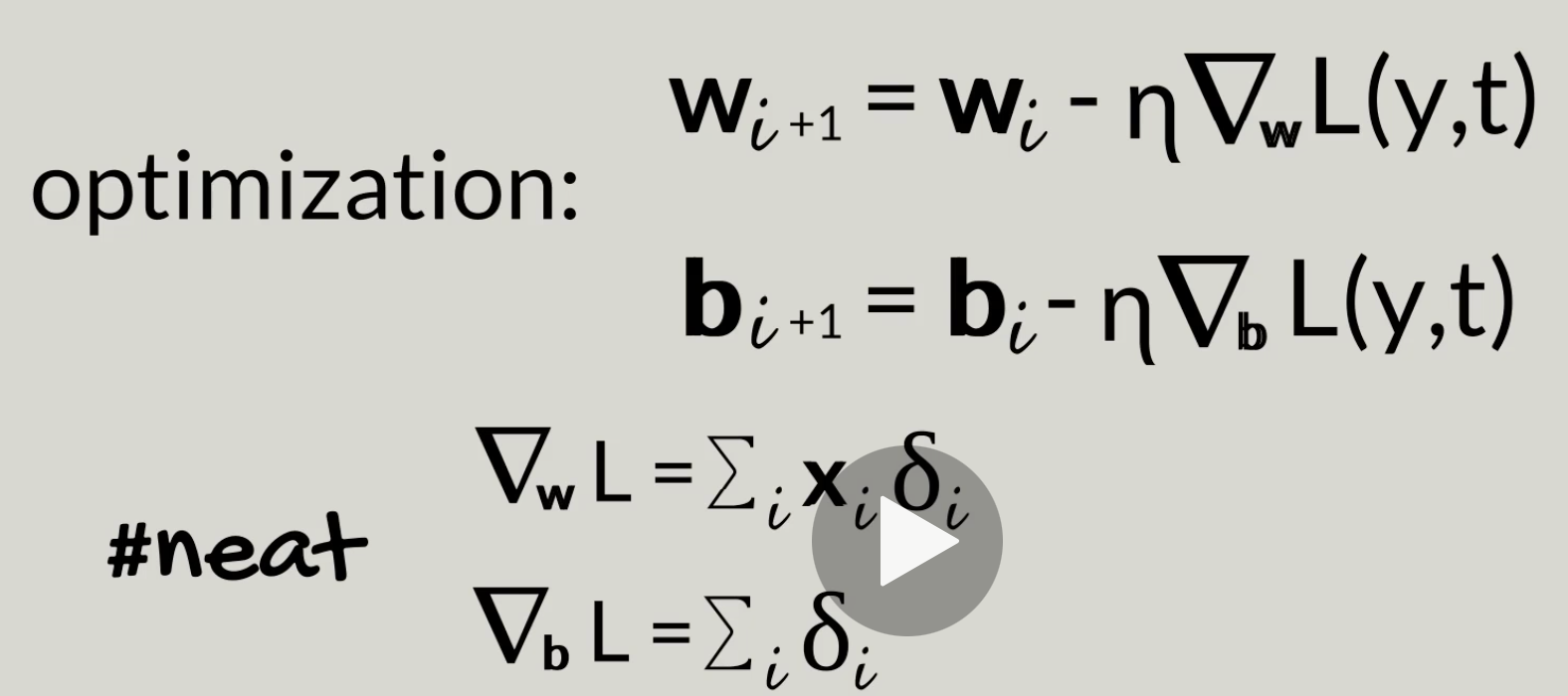Training an algorithm involes four ingredients:
- Data
- Model
- Objective function: We put data input a Model and get output out of it. The value we call it as 'lost'. We want to minimize the 'lost' value.
- Optimization algorithm: For example the linear model, we will try to optimize y = wx + b, 'w' & 'b' so that it will minimize the 'lost' value.
Repeat the process...
Three types of machine learning:
Supervised: Give feedback
- Classification: outputs are categories: cats or dogs
- Regression: output would be numbers.
Unsupervised: No feedback, find parttens
Reinforcement: Train the algorithm to works in a enviorment based on the rewords it receives. (Just like training your dog)
Linear Model:
f(x) = x * w + b
x: input
w: coefficient / weight
b: intercept / bias
Linear Model: Multi inputs:
x, w are both vectors:
x: 1 * 2
w: 2 * 1
f(x): 1 * 1
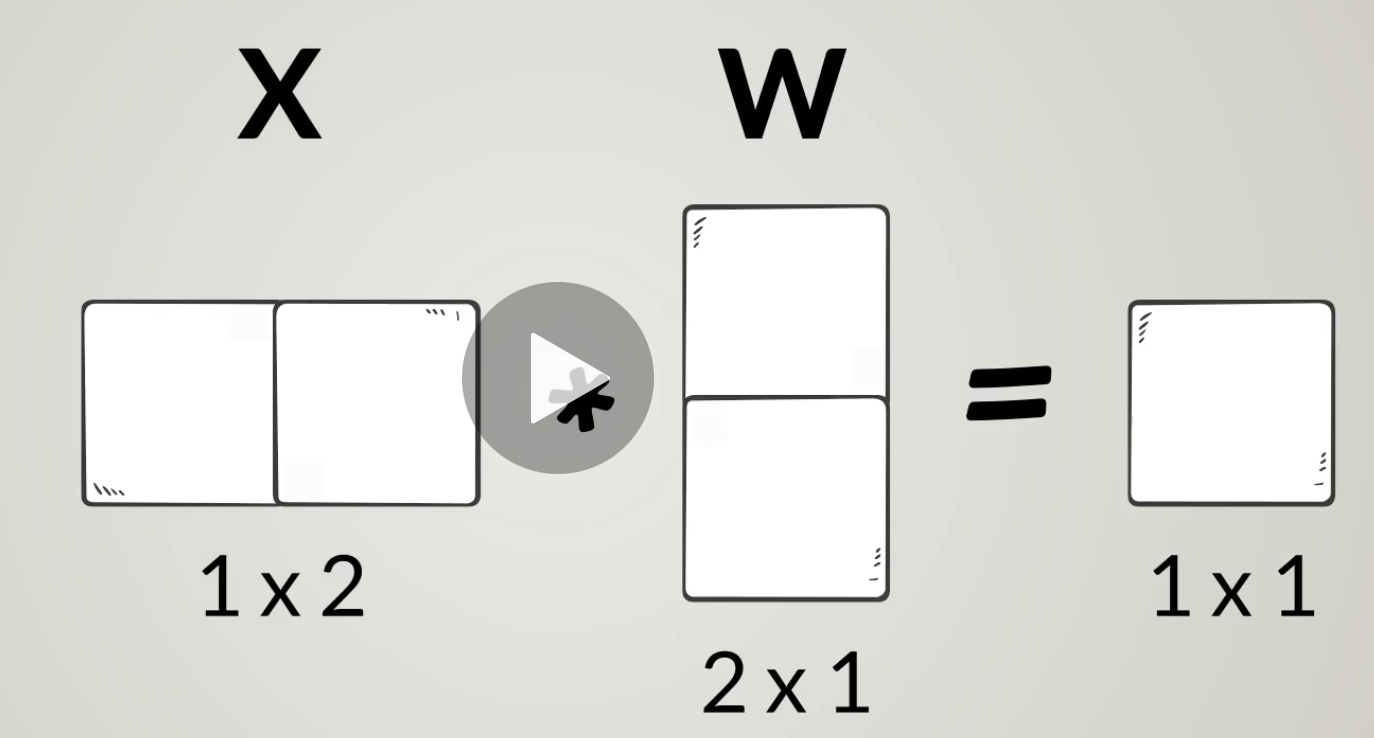
Notice that the lienar model doesn't chage, it is still:
f(x) = x * w + b
Lienar Model: multi inputs and multi outputs:

For 'W', the first index is always the same as X; the second index is always the same as ouput Y.
If there is K inputs and M outputs, the number of Weigths would be K * M
The number of bias is equal to the number of ouputs: M.
N * M = (N * K) * (K * M) + 1 * M
Each model is determined by its weights and biases.
Objection function:
Is the measure used to evaluate how well the model's output match the desired correct values.
- Loss function: the lower the loss function, the higher the level of accuracy (Supervized learning)
- Reward function: the hight of the reward function, the higher the level of accuracy (Reubfircement learning)
Loss functions for Supervised learning:
- Regression: L2-NORM

- Classification: CROSS-ENTROPY
Expect cross-entropy should be lower.

Optimization algorithm: Dradient descent


Until one point, the following value never update anymore.
The picture looks like this:
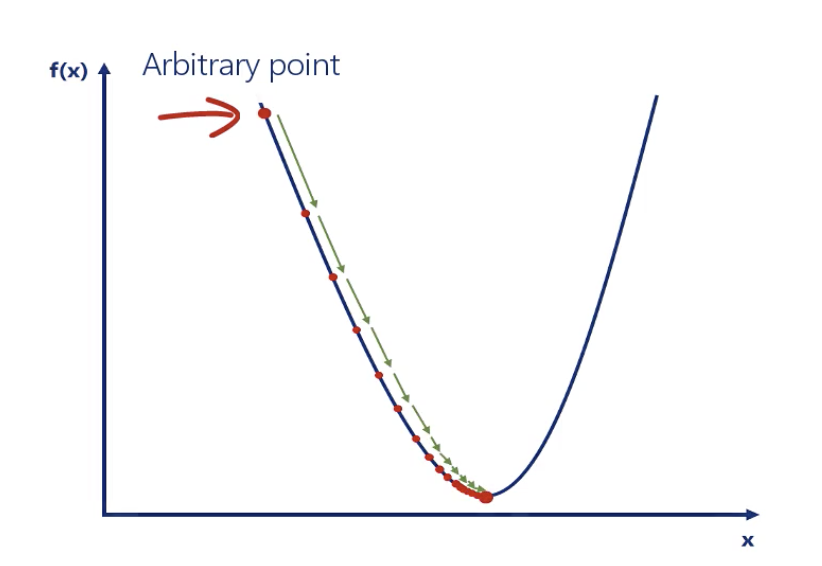
Generally, we want the learning rate to be:
High enough, so we can reach the closest minimum in a rational amount of time
Low enough, so we don't oscillate around the minimum

N-parameter gradient descent