:在ELM中先将训练样本导入,然后根据随机设置的输入层与隐层的权值Wi以及阈值Bi,然后再测试的时候不改变训练时候自动产生的Wi以及Bi,进行测试在于自己的结果进行比对从而得到测试误差。同样的在训练的时候也是如此来得到训练误差
训练模型如下:
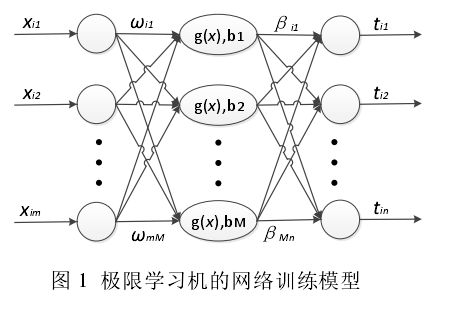
m为输入层神经元个数,M为隐层神经元的个数,n为输出层神经元的个数,g()为隐层神经元你的激励函数,b为隐层神经元你的阈值,(xi,ti)为训练样本
极限学习机的训练模型的数学表达式:
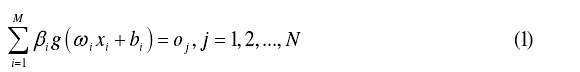
wi=[w1i,w2i......wmi]为输入层与隐层的权值向量; 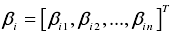 为输出层与隐层的权向量;
为输出层与隐层的权向量; 
极限学习机的代价函数E可表示为:
其中s=(wi,bi,i=1,2,3,......M)。黄广斌等人提出通过最小会待见函数的值来计算出输出函数与隐含层的权值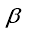 ,也就是最小化误差,使得训练的结果与实际的结果之间的差别变小,也就训练的越来越接近真实的结果。实际应用中,如果HHT非奇异,
,也就是最小化误差,使得训练的结果与实际的结果之间的差别变小,也就训练的越来越接近真实的结果。实际应用中,如果HHT非奇异,
![]() 为H矩阵的广义矩阵,而H矩阵是神经网络的隐层矩阵。O为预测目标值得向量。有岭回归理论可以知道,增加正常数1/C,可以使得结果更加稳定且具备更好的泛化能力也就是
为H矩阵的广义矩阵,而H矩阵是神经网络的隐层矩阵。O为预测目标值得向量。有岭回归理论可以知道,增加正常数1/C,可以使得结果更加稳定且具备更好的泛化能力也就是
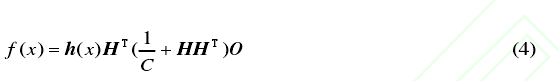
岭回归是对最小二乘的一种补充,可以降低“病态矩阵”的概率,损失了无偏性,以换取数值的高稳定性。
(1)最小二乘法:
最小二乘法的本质是什么? - 知乎
https://www.zhihu.com/question/37031188
阅读理解:就是一种确保真值与与测试值得误差之和尽量的小
(2)岭回归理论
岭回归_百度百科
https://baike.baidu.com/item/%E5%B2%AD%E5%9B%9E%E5%BD%92/554917?fr=aladdin
叙述了岭回归和最小二乘的关系,也就在最小二乘使用残差最小化的计算中,又重新加入了另外的一个矩阵。从而改变了最小二乘的无偏差估计。
(3)病态矩阵
Condition number - Wikipedia
https://en.wikipedia.org/wiki/Condition_number