数据结构与算法概述
数据结构的定义
我们如何把现实中大量而且非常复杂的问题以特定的数据类型(个体)和特定的存储结构(个体的关系)保存到相应的主存储器(内存)中,以及在此基础上为实现某个功能而执行的相应操作,这个相应的操作也叫做算法。
数据结构 == 个体 + 个体关系
算法 == 对存储数据的操作
数据结构的特点
数据结构是软件中最核心的课程。
程序 = 数据的存储 + 数据的操作 + 可以被计算机执行的语言。
算法
衡量算法的标准
- 时间复杂度 指的是大概程序执行的次数,而非程序执行的时间。
- 空阿金复杂度 值得是程序执行过程中,大概缩占用的最大内存。
- 难易程度
- 健壮性
需要熟练掌握的算法
常见的排序
- 冒泡排序
- 选择排序
- 插入排序
- 快速排序
- 归并排序
- 希尔排序
- 计数排序
常见的查找
- 顺序查找
- 二分法查找
其他的算法
- 贪心算法
- 递归算法
线性结构
比较通俗的讲,把所有的节点用一根线串起来的结构就称之为线性结构。线性结构分为两种方式:数组、链表。
数组与链表的区别
数组需要一块连续的内存空间来存储,堆内存的要求比较高。如果我们申请一个100M大小的数组,当内存中没有连续的、足够大的空间时,即使内存的剩余可用空间大于100M,任然会申请失败。而链表恰恰相反,它并不需要一块连续的内存空间,他通过“指针”将一组零散的内存块串联起来使用,所以申请的是大小是100M的链表,name根本不会有问题。
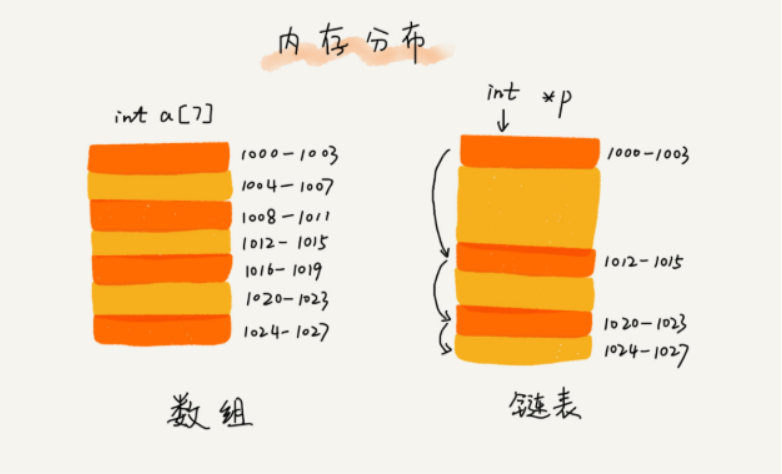
连续存储(数组)
数组,在python语言中成为列表,是一种基本的数据结构类型。
列表的优缺点
- 优点:
- 存取速度快
- 缺点:
- 事先需要知道数组的长度
- 需要大块的连续内存
- 插入删除非常的慢,效率极低
注:列表的其他问题,请百度python基础。
离散存储(链表)
链表的定义
- n个节点离散分配
- 彼此通过指针相连
- 每个节点都有一个前驱节点,每个节点只有一个后续节点
- 首节点没有前驱节点,尾节点没有后续节点
链表的优缺点
- 优点:
- 空间没有限制,插入删除元素很快
- 缺点:
- 查询比较慢
链表的结构
链表的及诶单结构如下:

data为自定义的数据,next为下一个节点的地址。
链表的专业术语
- 首节点:第一个有效节点。
- 尾节点:最后一个有效节点。
- 头结点:第一个有效节点之前的那个节点,头结点并不存储任何数据,目的是为了方便对链表的操作。
- 头指针:指向头结点的指针变量。(上图在头结点的左侧,未画出)
- 尾指针:指向尾节点的指针变量。
链表的分类
- 单链表
- 双链表 每一个节点有两个指针域
- 循环链表 能通过任何一个节点找到其他所有的节点
- 非循环列表
链表的算法
- 增加
- 删除
- 修改
- 查找
- 总长度
Python语言实现单链表的增删查
在Python语言中用面向对象组合的方式,代替指针指向,更加的方便,简单,容易理解。
# Use The Linked List sort Liangshan Po 108 Heroes
#
class Hero():
def __init__(self, no=None, name=None, nick_name=None, next=None):
self.no = no
self.name = name
self.nick_name = nick_name
self.next = next
def add_hero(head, hero):
current_position = head
while current_position.next and hero.no > current_position.next.no:
current_position = current_position.next
hero.next = current_position.next
current_position.next = hero
def get_all(head):
current_position = head
while current_position.next:
print("编号:%s,姓名:%s,外号:%s" % (
current_position.next.no, current_position.next.name, current_position.next.nick_name))
current_position = current_position.next
def delete_hero(head, hero):
current_position = head
if current_position.next:
while current_position.next and current_position.next.no < hero.no:
current_position = current_position.next
current_position.next = current_position.next.next
else:
print("链表为空")
head = Hero()
hero = Hero(1, '宋江', '及时雨')
# hero1 = Hero(2, '卢俊义', '玉麒麟')
# hero2 = Hero(3, '吴用', '智多星')
# hero3 = Hero(5, '林冲', '豹子头')
# hero4 = Hero(4, '公孙胜', '入云龙')
# add_hero(head, hero)
# add_hero(head, hero1)
# add_hero(head, hero2)
# add_hero(head, hero3)
# add_hero(head, hero4)
# get_all(head)
print("---------------------")
delete_hero(head, hero)
get_all(head)
双向链表
双链表中的每个节点有两个指针:一个指针指向后面节点,另一个指向前面节点。
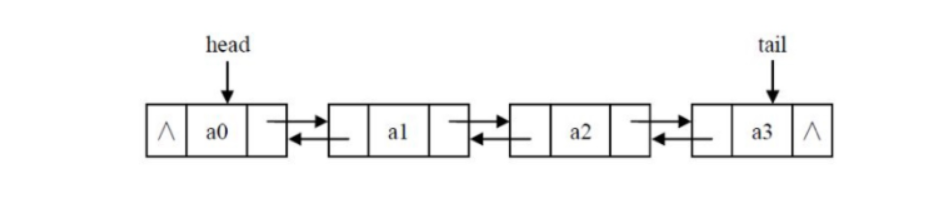
class Node(object):
def __init__(self, data=None):
self.data = data
self.next = None
self.prior = None
双向链表的操作:
- 插入:
p.next = curNode.next
curNode.next.prior = p
curNode.next = p
p.prior = curNod
- 删除:
p = curNode.next
curNode.next = p.next
p.next.prior = curNode
del p
循环链表
循环链表是另一种形式的链式存储结构。它的特点是表中最后一个节点的指针域指向头结点,整个链表形成一个环。
数组与链表的性能比较
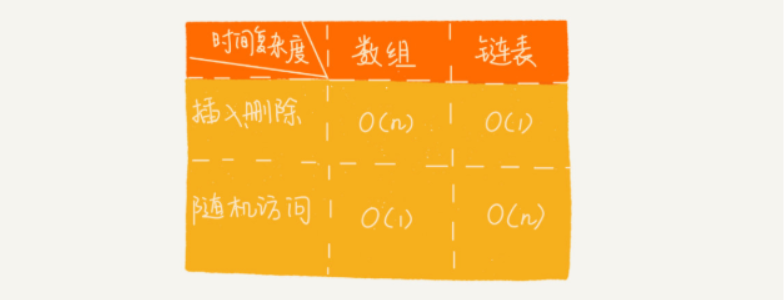
线性结构的两种应用方式
线性结构的两种应用方式:栈、队列
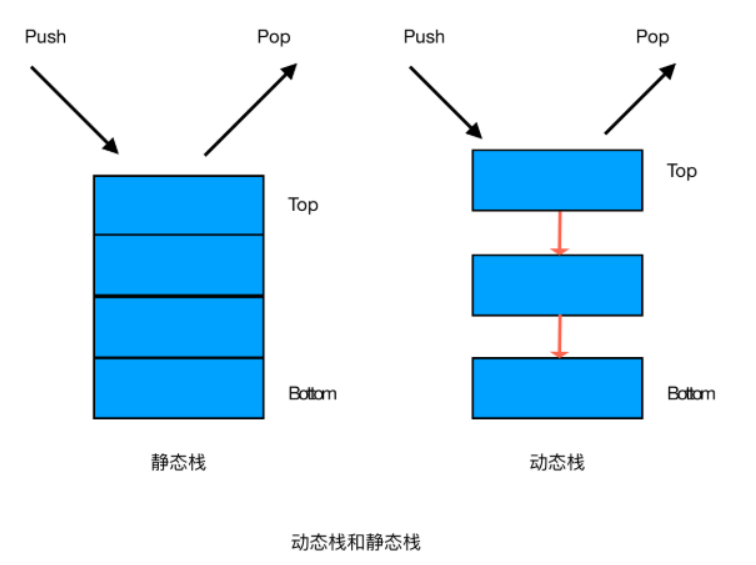
栈
栈的定义:
一种可以实现“先进后出”的存储结构。栈类似于一个箱子,先放进去的书,最后才能取出来,同理,后翻进去的书,先取出来。
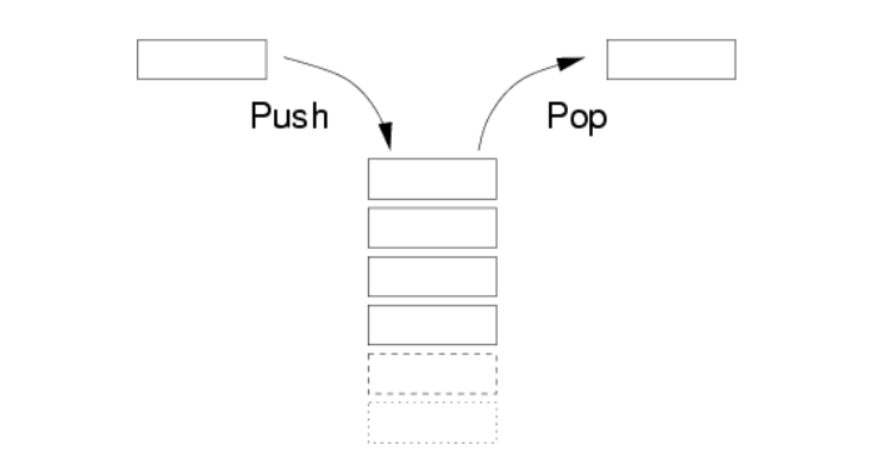
栈的分类:
- 静态栈
- 静态栈的核心是数组,类似于一个连续内存的数组,我们只能操作其栈顶元素。
- 动态栈
- 动态栈的核心是链表
栈的应用:
- 函数调用(递归)
- 浏览器的前进后退
- 表达式求职 (1+2 -5*6)
- 内存分配
队列
队列的定义:
一种可以实现“先进先出”的出具结构。
队列的分类:
- 链式队列
- 静态队列
队列的应用
所有和时间有关的操作都和队列有关。
冒泡排序
冒泡排序:
①、比较相邻的元素。如果第一个比第二个大,就交换他们两个。
②、对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。这步做完后,最后的元素会是最大的数(也就是第一波冒泡完成)。
③、针对所有的元素重复以上的步骤,除了最后一个。
④、持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
#Bubble Sort
def Bubble_sort(li):
for i in range(len(li)-1):
for k in range(len(li)-i-1):
if li[k] > li[k+1]:
li[k],li[k+1] = li[k+1],li[k]
li = [3,52,3,6,1,8,2,6,1,8,95,23]
Bubble_sort(li)
print(li)
选择排序
选择排序是每一次从待排序的数据元素中选出最小的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完。
分为三步:
①、从待排序序列中,找到关键字最小的元素
②、如果最小元素不是待排序序列的第一个元素,将其和第一个元素互换
③、从余下的 N - 1 个元素中,找出关键字最小的元素,重复(1)、(2)步,直到排序结束
#选择排序
def select_sort(li):
for i in range(len(li)-1):
min = li[i]
for j in range(i+1,len(li)):
if min > li[j]:
li[i],li[j],min = li[j],li[i],li[j]
li = [3,52,3,6,1,8,2,6,1,8,95,23,6]
select_sort(li)
print(li)
插入排序
直接插入排序基本思想是每一步将一个待排序的记录,插入到前面已经排好序的有序序列中去,直到插完所有元素为止。
#插入排序
def insert_sort(li):
for i in range(1,len(li)):
tmp = li[i]
j = i-1
while j>=0 and li[j] > tmp:
li[j+1] = li[j]
j= j-1
li[j+1] = tmp
li = [3,5,2,1]
insert_sort(li)
print(li)
快速排序
一、先通过第一趟排序,将数组原地划分为两部分**,**首先任意选取一个数据(通常选用数组的第一个数)作为关键数据,然后将所有比它小的数都放到它前面,所有比它大的数都放到它后面,
二、通过递归的处理, 再对原数组分割的两部分分别划分为两部分,同样是使得其中一部分的所有数据都小于另一部分的所有数据。 这个时候原数组被划分为了4份
三、就1,2被划分后的最小单元子数组来看,它们仍然是无序的,但是! 它们所组成的原数组却逐渐向有序的方向前进。
四、这样不断划分到最后,数组就被划分为多个由一个元素或多个相同元素组成的单元,这样数组就有序了。
def get_mid(li,left,right):
tmp = li[left]
while left < right:
#右侧比较
while left < right and li[right] >= tmp:
right-=1
li[left] = li[right]
#左侧比较
while left < right and li[left] <= tmp:
left+=1
li[right] = li[left]
li[left] = tmp
return left
def quick_sort(li,left,right):
if left < right:
mid = get_mid(li,left,right)
quick_sort(li,left,mid)
quick_sort(li,mid+1,right)
li = [28, 36, 91, 80, 23, 24, 84, 69, 96, 29, 16, 63, 13, 89, 28, 25, 16, 97, 71, 15, 92, 47, 21, 55, 76, 42, 32, 78, 26]
quick_sort(li,0,len(li)-1)
print(li)
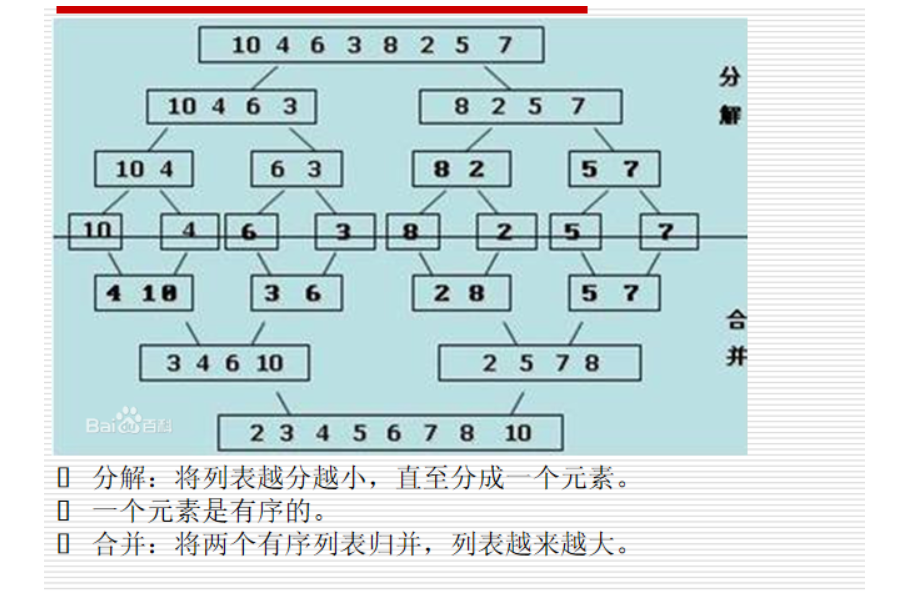
归并排序
def merge(li,low,mid,high):
i = low
j = mid + 1
tmp = []
while i <= mid and j <=high:
if li[i] < li[j]:
tmp.append(li[i])
i+=1
else:
tmp.append(li[j])
j+=1
while i <= mid:
tmp.append(li[i])
i+=1
while j <= high:
tmp.append(li[j])
j+=1
li[low:high+1] = tmp
#归并排序
def merge_sort(li,low,high):
if low < high:
mid = (low + high) // 2
merge_sort(li,low,mid)
merge_sort(li,mid+1,high)
merge(li,low,mid,high)
li = [3,52,3,6,1,8,2,6,1,8,95,23]
merge_sort(li,0,len(li)-1)
print(li)
希尔排序
直接插入排序基本思想是每一步将一个待排序的记录,插入到前面已经排好序的有序序列中去,直到插完所有元素为止。
我们可以分析一下这个直接插入排序,首先我们将需要插入的数放在一个临时变量中,这也是一个标记符,标记符左边的数是已经排好序的,标记符右边的数是需要排序的。接着将标记的数和左边排好序的数进行比较,假如比目标数大则将左边排好序的数向右边移动一位,直到找到比其小的位置进行插入。
这里就存在一个效率问题了,如果一个很小的数在很靠近右边的位置,比如上图右边待排序的数据 1 ,那么想让这个很小的数 1 插入到左边排好序的位置,那么左边排好序的数据项都必须向右移动一位,这个步骤就是将近执行了N次复制,虽然不是每个数据项都必须移动N个位置,但是每个数据项平均移动了N/2次,总共就是N2/2,因此插入排序的效率是O(N2)。
计数排序
创建一个列表,用来统计每个数出现的次数。
import random
#Count Sort
def count_sort(li):
element_list = []
if not li:
return
for i in range(max(li)+1):
element_list.append(0)
for j in range(len(li)):
if li[j] == i:
element_list[i]+=1
# li.clear()
i = 0
for index,val in enumerate(element_list):
# while val > 0:
# li.append(index)
# val-=1
for m in range(val):
li[i] = index
i+=1
li = [1,2,2,1,3,5,2,1,2,2,3,4,192,2,1]
count_sort(li)
print(li)
普通查找
def normal_select(li,target):
for i in range(len(li)):
if li[i] == target:
return i
return None
二分法查找
#Select an Element from a sorted list
def dichotomy(sorted_li,left,right,target):
"""
:param sorted_li: the target list
:param left: the target list's the most left index
:param right: the target list's the most right index
:param target: select element
:return: the target's index in sorted_li
"""
mid = (left + right) // 2
if sorted_li[mid] > target:
#要取的值在左侧
return dichotomy(sorted_li,left,mid-1,target)
elif sorted_li[mid] < target:
return dichotomy(sorted_li,mid+1,right,target)
else:
return mid
li = [1,2,3,5,6,7,9,10,12]
print(dichotomy(li,0,len(li)-1,7))
贪心算法(分糖果案例)
#Greedy Algorithm
#The Problem for Branch Candy
"""
已知有一些孩子和一些糖果,每个孩子都有需求因子g,每个糖果有大小s;如果某个糖果的大小s>=某个孩子的需求因子时,代表该糖果可以满足该孩子,使用这些糖果,最多可以满足多少孩子?(注意:某个孩子最多只能被一块糖果满足)
1、举个实例
孩子的需求因子为g = [5, 10, 2,9,15,9];糖果的大小数组为:s = [6,1,20,3,8],那么,这种情况下,最多可以,满足3个孩子。
"""
def greedy_algorithm(child_list,candy_list):
child_list.sort()
candy_list.sort()
count = 0
child = 0
candy = 0
while child < len(child_list) and candy < len(candy_list):
#candy can eat for this child
if child_list[child] <= candy_list[candy]:
count+=1
child+=1
candy+=1 #however the candy can eat or can not eat ,it always reduce
return count
g = [10,9,8,7] #child_list
s = [5,6,7,8] #candy_list
print(greedy_algorithm(g,s))
递归算法(阶乘案例)
#Use Recursion function Solve Factorial Problem
def factorial(n):
if n == 1 or n ==0:
return 1
if n < 0:
raise ValueError('阶层必须是自然数')
else:
return n*factorial(n-1)
print(factorial(-1))