牛客寒假算法基础集训营1 D 小a与黄金街道

  小a与黄金街道

 

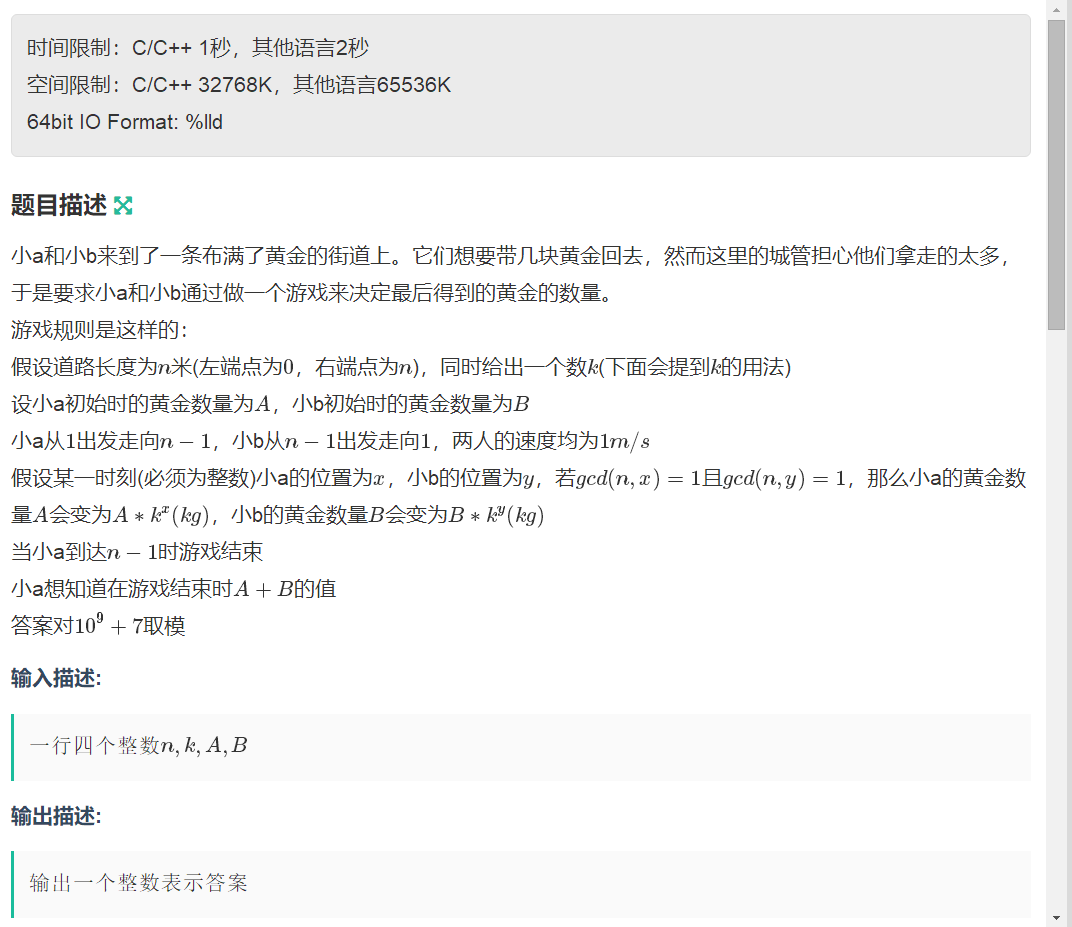
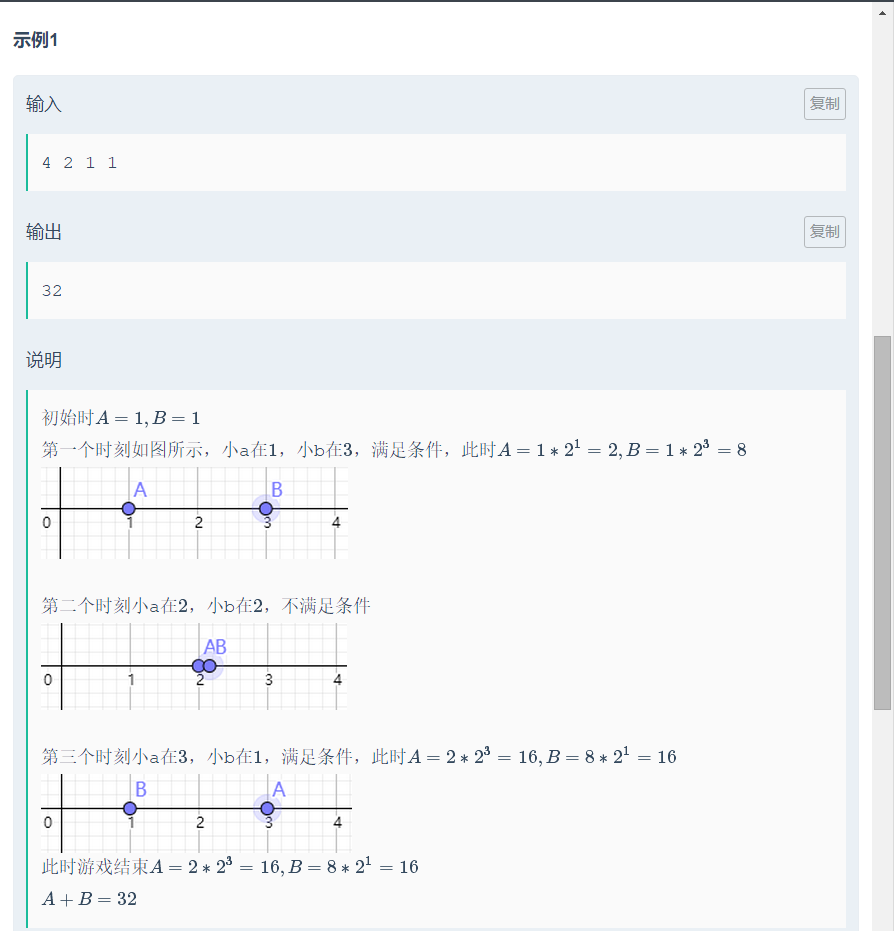
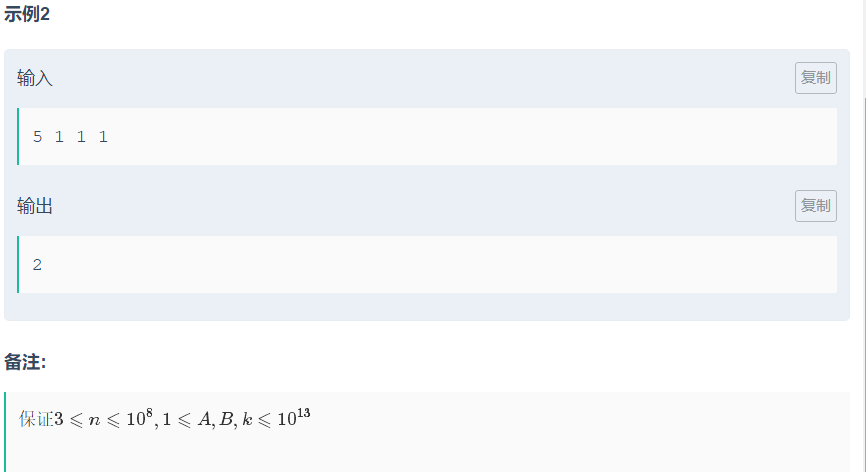
链接：https://ac.nowcoder.com/acm/contest/317/D

题解：

附上欧拉函数模板：  

(1)直接求小于或等于n,且与n互质的个数:

  int Euler(int n)

{

    int ret=n;

    for(int i=2;i<=sqrt(n);i++)

     if(n%i==0)

      {

        ret=ret/i*(i-1);//先进行除法防止溢出(ret=ret*(1-1/p(i)))

        while(n%i==0)

          n/=i;

     }

    if(n>1)

          ret=ret/n*(n-1);

        return ret;

}

筛选模板:求[1,n]之间每个数的质因数的个数

#define size 1000001

int euler[size];

void Init()

{   memset(euler,0,sizeof(euler));

          euler[1]=1;

    for(int i=2;i<size;i++)

       if(!euler[i])

       for(int j=i;j<size;j+=i)

       {

              if(!euler[j])

               euler[j]=j;

               euler[j]=euler[j]/i*(i-1);//先进行除法是为了防止中间数据的溢出

         }

}

import java.util.Scanner;

public class Main{
    static int maxn = 100010;
    static int [] euler = new int[maxn];
    /*static void init() {
        euler[1] = 1;
        for(int i=2;i<maxn;i++) {
            if(euler[i]==0) {
                for(int j=i;j<maxn;j+=i) {
                    if(euler[j]==0) {
                        euler[j] = j;
                    }
                    euler[j] = euler[j]/i*(i-1);
                }
            }
        }
    }*/
    static long init(long x) {
        long ret = x;
        for(int i=2;i*i<=x;i++) {
            if(x%i==0) {
                ret = ret/i*(i-1);
                while(x%i==0) {
                    x/=i;
                }
            }            
        }
        if(x>1)
            ret = ret/x*(x-1);
        return ret;
    }
    static long powmod(long a,long b,long mo) {
        long ans = 1;
        while(b!=0) {
            if((b&1)==1) {
                ans = (ans*a)%mo;
            }
            a = (a*a)%mo;
            b>>=1;
        }
        return ans;
    }
    public static void main(String[] args) {
        Scanner cin = new Scanner(System.in);
        int n,k;
        long A,B;
        n = cin.nextInt();
        k = cin.nextInt();
        A = cin.nextLong();
        B = cin.nextLong();
        long ans = (A+B)*powmod(k, init(n)/2*n, 1000000007)%1000000007;
        System.out.println(ans);
    }    
}