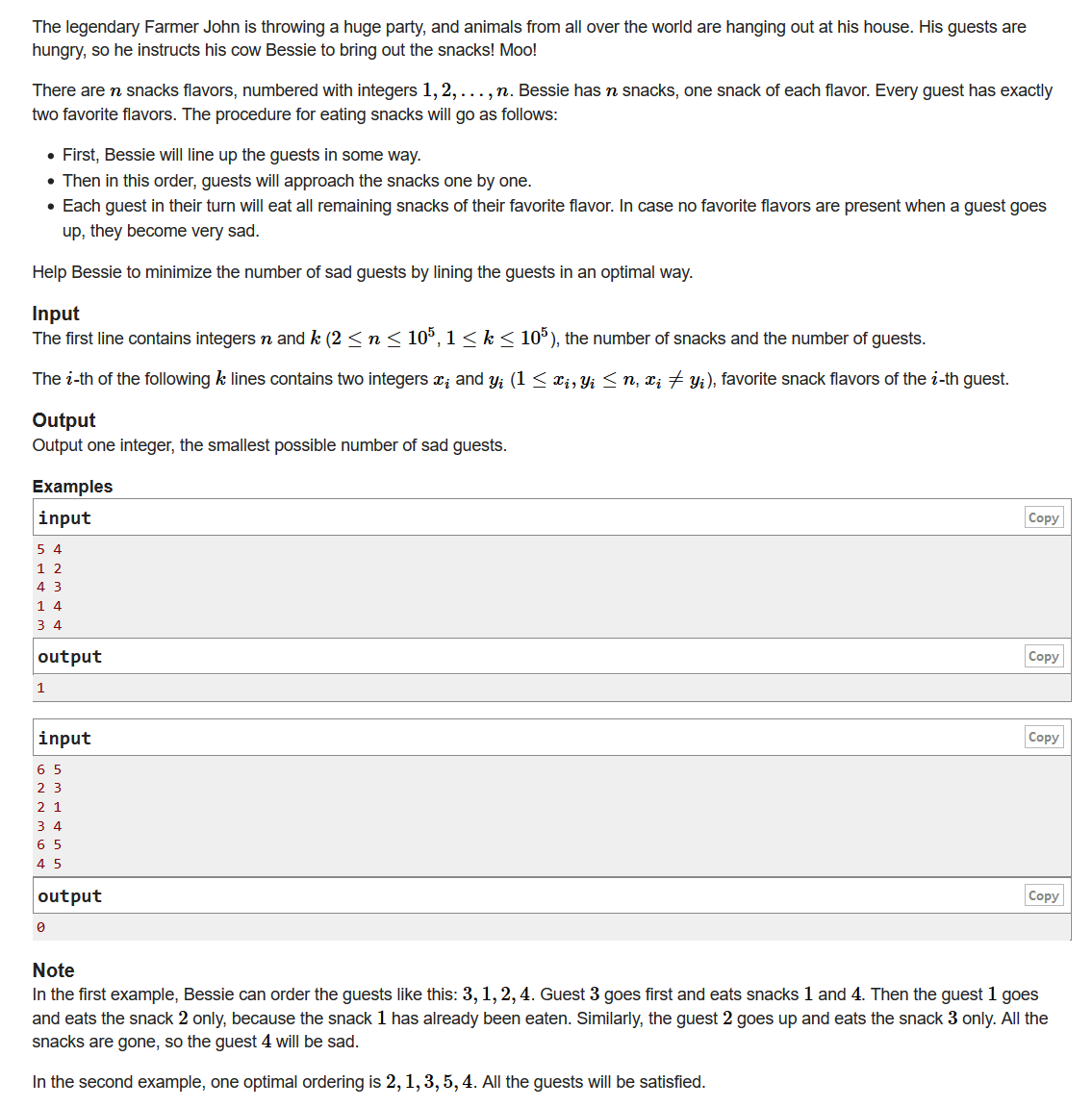
题意:有n种小吃,m个人,每个人有两种喜欢的小吃,当一个人遇到两种自己都喜欢的小吃,可以都吃掉,问在最优的吃小吃顺序下,不能吃到自己喜欢的小吃的人数最少是多少?
题解:把n种小吃当作n个点,m个人当作m条边,每个连通图里面第一个吃的人,一定是可以吃两种自己喜欢的小吃。每次判断这条边是否在已有的联通图里面,对已经在连通图里面的边,是一定不能吃到小吃,若不在连通图里面,则一定可以吃到小吃,用cnt统计可以吃到小吃的人数,最后m-cnt就是答案
#include<iostream> #include<string.h> #include<string> #include<algorithm> using namespace std; int p[1000005], r[1000005]; int n,t=0; void init()//初始化集合,每个元素的老板都是自己 { for (int i = 1; i <= n; i++) { p[i] = i; } } int find(int x)//查找元素x的老板是谁 { if (x == p[x]) return x; else return p[x] = find(p[x]); } void join(int x, int y)//合并两个集合 { int xRoot = find(x); int yRoot = find(y); if (xRoot == yRoot) //老板相同,不合并 return; //cnt=cnt-1; if (r[xRoot] < r[yRoot]) //r[i]是元素i所在树的高度,矮树的根节点认高树的根节点做老板 p[xRoot] = yRoot; else if (r[xRoot] > r[yRoot]) p[yRoot] = xRoot; else { p[yRoot] = xRoot;//树高相同,做老板的树高度要加一 r[xRoot]++; } } bool sameRoot(int x, int y)//查询两个元素的老板是否相同 { return find(x) == find(y); } //这里也可以用cnt求不同子集个数,初始化cnt=n,每加入一条边,cnt=cnt-1; int main() { ios::sync_with_stdio(false); int m,cnt=0; cin>>n>>m; init(); for(int i=0;i<m;i++) { int x,y; cin>>x>>y; if(!sameRoot(x,y)) { join(x,y); cnt++; } } cout<<m-cnt<<endl; return 0; }