Cactus
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 1907 Accepted Submission(s): 879
Problem Description
1. It is a Strongly Connected graph.
2. Each edge of the graph belongs to a circle and only belongs to one circle.
We call this graph as CACTUS.
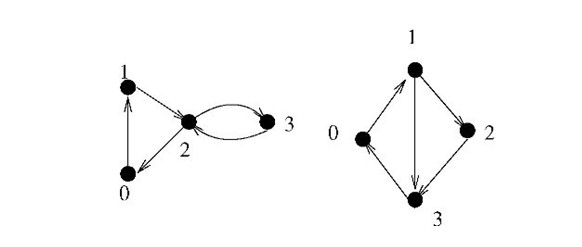
There is an example as the figure above. The left one is a cactus, but the right one isn’t. Because the edge (0, 1) in the right graph belongs to two circles as (0, 1, 3) and (0, 1, 2, 3).
2. Each edge of the graph belongs to a circle and only belongs to one circle.
We call this graph as CACTUS.

There is an example as the figure above. The left one is a cactus, but the right one isn’t. Because the edge (0, 1) in the right graph belongs to two circles as (0, 1, 3) and (0, 1, 2, 3).
Input
The input consists of several test cases. The first line contains an integer T (1<=T<=10), representing the number of test cases.
For each case, the first line contains a integer n (1<=n<=20000), representing the number of points.
The following lines, each line has two numbers a and b, representing a single-way edge (a->b). Each case ends with (0 0).
Notice: The total number of edges does not exceed 50000.
For each case, the first line contains a integer n (1<=n<=20000), representing the number of points.
The following lines, each line has two numbers a and b, representing a single-way edge (a->b). Each case ends with (0 0).
Notice: The total number of edges does not exceed 50000.
Output
For each case, output a line contains “YES” or “NO”, representing whether this graph is a cactus or not.
Sample Input
2
4
0 1
1 2
2 0
2 3
3 2
0 0
4
0 1
1 2
2 3
3 0
1 3
0 0
Sample Output
YES
NO
Author
alpc91
Source
题意:
判断有向图是否是仙人掌图。仙人掌图:是强连通图,每条边最多只能属于一个圈。
仙人掌图性质:1.仙人掌图的dfs树没有横向边。2.lowlink[v]<pre[u],v是u的儿子。3.设某点u有a个儿子的lowlink值小于pre[u],有b条逆向边,则a+b<2;
代码:
#include<iostream> #include<cstdio> #include<cstring> #include<vector> #include<stack> using namespace std; const int maxn=20004; int t,n,flag; vector<int>g[maxn];//g保存原始图 int pre[maxn],lowlink[maxn],sccno[maxn],dfs_clock,scc_cnt,vis[maxn]; //pre[u]为节点u的搜索次序编号;lowlink[u]为u或u的子树能够追溯到的最早的栈中结点的编号 //sccno[i]为i所在的scc的编号;scc_cnt为scc计数器 stack<int>s;//保存当前scc中的节点 void dfs(int u) { pre[u]=lowlink[u]=++dfs_clock;//设置节点u次序编号lowlink初值 s.push(u); int sum=0; for(int i=0;i<(int)g[u].size();i++){ int v=g[u][i]; if(vis[v]) {flag=false;return;}//性质1 if(!pre[v]){ dfs(v); lowlink[u]=min(lowlink[u],lowlink[v]); if(lowlink[v]>pre[u]) {flag=false;return;}//性质2 if(lowlink[v]<pre[u]) sum++;//性质3 if(sum>1) {flag=false;return;} } else if(!sccno[v]){ lowlink[u]=min(lowlink[u],pre[v]); sum++;//性质3 if(sum>1) {flag=false;return;} } } if(lowlink[u]==pre[u]){ //如果节点u是强连通分量的根 scc_cnt++; for(;;){ int x=s.top();//x退栈为该强连通分量中的一个点 s.pop(); sccno[x]=scc_cnt; if(x==u) break; } } vis[u]=true; } void find_scc() { dfs_clock=scc_cnt=0; flag=true; memset(pre,0,sizeof(pre)); memset(sccno,0,sizeof(sccno)); memset(vis,false,sizeof(vis)); for(int i=0;i<n;i++) if(!pre[i]) dfs(i); } int main() { scanf("%d",&t); while(t--){ scanf("%d",&n); int a,b; for(int i=0;i<=n;i++) g[i].clear();//记住向量清空 while(scanf("%d%d",&a,&b)){ if(a==0&&b==0) break; g[a].push_back(b); } find_scc(); if(flag) cout<<"YES "; else cout<<"NO "; } return 0; }