比赛连接戳这里^_^
我才不会说这是我出的题(逃)
周赛题解((2018.10.14))
(T1)
(25sim50)分做法(:)直接爆搜
作为一个良心仁慈又可爱的出题人当然(T1)要送分啦(qwq)
(100)分做法(:)
其实只需要看左上角就行了,因为题目描述写的很清楚,三个人的操作都是为了BLUESKY007能赢,所以游戏一定会结束,那么当横纵坐标最大的非(B)颜色方格变为(B)颜色时,可操作的方格范围显然是趋向收敛的,又因为操作规则的要求,左上角的方格在每次操作中都会按规则进行变换,当可操作范围收敛到左上角且左上角变为(B)颜色时,游戏结束,所以无论中间的操作是怎样进行的,最终左上角的方格一定会变为(B)颜色,而且进行操作的人数和操作变换长度相同,所以我们只需要判断左上角方格的颜色即可.
(T2)
(10)分做法(:)特判输出
毕竟数据范围给的那么小,(n,m)都(leq5),显然是送分的啊(qwq)
(20)分做法(:)爆搜
就是很裸的爆搜,连优化剪枝之类的高级操作都不需要.但是为什么(min(n,m)leq3)?这个看下面证明就知道了(qwq)
(100)分做法(:)结论
我们不妨设(n)为长,(m)为宽
- (mleq2:)显然对于任何一个位置,在图中都不存在另外一个位置使得两者之间相互可达,所以此时(n imes m)的所有位置都可以放置,此时答案为(n imes m)
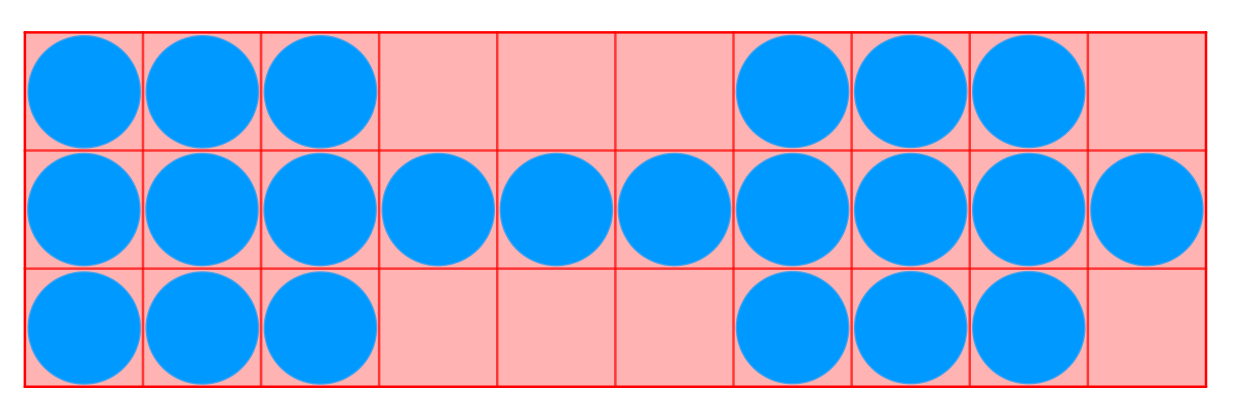
- (m=3:)对于一个(3 imes n)的图,其中对于第二行的所有点,在图中都不存在另外一个位置使得两者之间相互可达,所以第二行所有位置都可以放置,对于另外两行我们可以发现,((1,1))和((3,4))只能有一个位置放置,((1,2))和((3,5)),((1,3))和((3,6)),((3,1))和((1,4)),((3,2))和((1,5)),((3,3))和((1,6))同理.于是当我们最大化放置个数时,每相邻的六列的放置总是相同的且任意相邻六列至多可以放置(12)个,所以当我们按如图所示的方式开始时会达到最大值,此时答案为(n+6 imeslfloorfrac{n}{6}
floor+2 imesmin(n\%6,3))
- (m=4:)同样的,对于一个(4 imes n)的图,仍然满足相邻六列最多放置(12)个,但是对于不同的(n)存在不同的起始方案(:)
- (n\%6=0:)从任意列开始,此时答案为(2n)
- (n\%6in[1,2]:)从第(1)列开始,此时答案为(2n+2 imes(n\%6))
- (n\%6in[3,4]:)从第(6)列开始,此时答案为(2n+4)
- (n\%6=5:)从第(6)列开始,此时答案为(12lceilfrac{n}{6}
ceil)
所以如果(m=4),能考虑到以上情况的话自然就不是写爆搜的了,所以对爆搜的数据范围设置为(mleq3),否则会(WA)
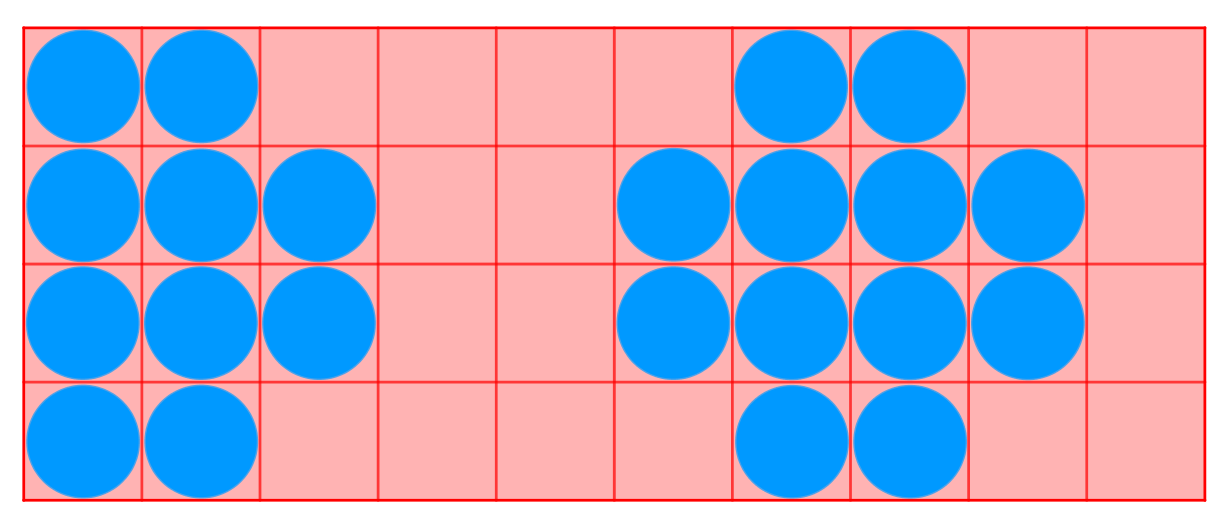
- (mgeq5:)如图为(n=7,m=5)时的放置方案,类似的,对于任意大小的图都可以进行类似的放置,此时答案为(lceilfrac{mn}{2} ceil)
(T3)
(20)分做法(:)直接输出(0)
根据样例解释,([0,1000])内不存在"好朋友",所以对于(20\%)数据(l_ileq r_ileq10^3)显然其中所有的询问答案均为(0),所以直接输出就能骗到(20)分
(40)分做法(:O(trlg(r)))逐个检验
(100)分做法(:O(tlg(r)))数位(DP)
因为"好朋友"的定义为含有"007",所以有很多情况都会被视为含有"007",例如"10707","17007"等,此时我们发现对于含有"007"的情况的讨论比较复杂,所以我们不妨讨论不含"007"的情况,也即对于任意的含有(7)的数,其中每一个(7)前都至多有(2)个(0),由此可以设(f_{ij})表示在前(i)位有(j)个(0)的数的个数,在数位(DP)过程中存当前位置和已有的(0)的个数,显然在(0)的个数(geq2)时,后面的数位上都不可能再有(7).在求出不含"007"的数之后,用区间(l_i,r_i)上数的个数减去不含"007"的数的个数即可得到在(l_i,r_i)上含有"007"的数的个数