poj1408——叉积求多边形面积
Fishnet
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 1853 | Accepted: 1185 |
Description
A fisherman named Etadokah awoke in a very small island. He could see calm, beautiful and blue sea around the island. The previous night he had encountered a terrible storm and had reached this uninhabited island. Some wrecks of his ship were spread around him. He found a square wood-frame and a long thread among the wrecks. He had to survive in this island until someone came and saved him.
In order to catch fish, he began to make a kind of fishnet by cutting the long thread into short threads and fixing them at pegs on the square wood-frame. He wanted to know the sizes of the meshes of the fishnet to see whether he could catch small fish as well as large ones.
The wood frame is perfectly square with four thin edges on meter long: a bottom edge, a top edge, a left edge, and a right edge. There are n pegs on each edge, and thus there are 4n pegs in total. The positions of pegs are represented by their (x,y)-coordinates. Those of an example case with n=2 are depicted in figures below. The position of the ith peg on the bottom edge is represented by (ai,0). That on the top edge, on the left edge and on the right edge are represented by (bi,1), (0,ci) and (1,di), respectively. The long thread is cut into 2n threads with appropriate lengths. The threads are strained between (ai,0) and (bi,1),and between (0,ci) and (1,di) (i=1,...,n).
You should write a program that reports the size of the largest mesh among the (n+1)2 meshes of the fishnet made by fixing the threads at the pegs. You may assume that the thread he found is long enough to make the fishnet and the wood-frame is thin enough for neglecting its thickness.
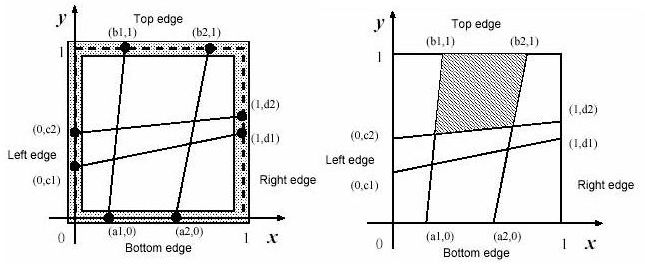
In order to catch fish, he began to make a kind of fishnet by cutting the long thread into short threads and fixing them at pegs on the square wood-frame. He wanted to know the sizes of the meshes of the fishnet to see whether he could catch small fish as well as large ones.
The wood frame is perfectly square with four thin edges on meter long: a bottom edge, a top edge, a left edge, and a right edge. There are n pegs on each edge, and thus there are 4n pegs in total. The positions of pegs are represented by their (x,y)-coordinates. Those of an example case with n=2 are depicted in figures below. The position of the ith peg on the bottom edge is represented by (ai,0). That on the top edge, on the left edge and on the right edge are represented by (bi,1), (0,ci) and (1,di), respectively. The long thread is cut into 2n threads with appropriate lengths. The threads are strained between (ai,0) and (bi,1),and between (0,ci) and (1,di) (i=1,...,n).
You should write a program that reports the size of the largest mesh among the (n+1)2 meshes of the fishnet made by fixing the threads at the pegs. You may assume that the thread he found is long enough to make the fishnet and the wood-frame is thin enough for neglecting its thickness.

Input
The input consists of multiple sub-problems followed by a line containing a zero that indicates the end of input. Each sub-problem is given in the following format.
n
a1 a2 ... an
b1 b2 ... bn
c1 c2 ... cn
d1 d2 ... dn
you may assume 0 < n <= 30, 0 < ai,bi,ci,di < 1
n
a1 a2 ... an
b1 b2 ... bn
c1 c2 ... cn
d1 d2 ... dn
you may assume 0 < n <= 30, 0 < ai,bi,ci,di < 1
Output
For each sub-problem, the size of the largest mesh should be printed followed by a new line. Each value should be represented by 6 digits after the decimal point, and it may not have an error greater than 0.000001.
Sample Input
2 0.2000000 0.6000000 0.3000000 0.8000000 0.1000000 0.5000000 0.5000000 0.6000000 2 0.3333330 0.6666670 0.3333330 0.6666670 0.3333330 0.6666670 0.3333330 0.6666670 4 0.2000000 0.4000000 0.6000000 0.8000000 0.1000000 0.5000000 0.6000000 0.9000000 0.2000000 0.4000000 0.6000000 0.8000000 0.1000000 0.5000000 0.6000000 0.9000000 2 0.5138701 0.9476283 0.1717362 0.1757412 0.3086521 0.7022313 0.2264312 0.5345343 1 0.4000000 0.6000000 0.3000000 0.5000000 0
Sample Output
0.215657 0.111112 0.078923 0.279223 0.348958
题意:如图,求图中面积最大的多边形的面积
思路:直接枚举i,j,求交点得到多边形的四个点,叉积法求面积

/** * Start at 21:20 * End at 22:40 * Problem: poj1408 * Author: __560 * */ #include<iostream> #include<cstdlib> #include<cstdio> #include<cstring> #include<algorithm> #include<math.h> using namespace std; const int maxn=1000100; const int INF=(1<<28); const double eps=0.00000000001; int n; struct Point { double x,y; friend double operator*(Point A,Point B) { return A.x*B.y-A.y*B.x; } friend Point operator-(Point A,Point B) { return {A.x-B.x,A.y-B.y}; } friend Point operator+(Point A,Point B) { return {A.x+B.x,A.y+B.y}; } }; Point A[maxn],B[maxn],C[maxn],D[maxn]; Point inter_point(Point A,Point B,Point C,Point D) { double a=fabs((B-A)*(C-A)); double b=fabs((B-A)*(D-A)); double x=(a*D.x+b*C.x)/(a+b); double y=(a*D.y+b*C.y)/(a+b); return {x,y}; } void solve() { double ans=0; A[0]=C[0]={0,0}; B[0]=C[n+1]={0,1}; D[0]=A[n+1]={1,0}; B[n+1]=D[n+1]={1,1}; for(int i=0;i<=n;i++){ for(int j=0;j<=n;j++){ Point a=inter_point(A[i],B[i],C[j],D[j]); Point b=inter_point(A[i+1],B[i+1],C[j],D[j]); Point c=inter_point(A[i],B[i],C[j+1],D[j+1]); Point d=inter_point(A[i+1],B[i+1],C[j+1],D[j+1]); double area=(b-a)*(d-a)/2.0+(d-a)*(c-a)/2.0; if(area>ans+eps) ans=area; //cout<<"a= "<<a.x<<" "<<a.y<<" "; //cout<<"i="<<i<<" j="<<j<<" area="<<area<<endl; } } printf("%.6f ",ans); } int main() { while(cin>>n,n){ for(int i=1;i<=n;i++){ scanf("%lf",&(A[i].x)); A[i].y=0; } for(int i=1;i<=n;i++){ scanf("%lf",&(B[i].x)); B[i].y=1; } for(int i=1;i<=n;i++){ scanf("%lf",&(C[i].y)); C[i].x=0; } for(int i=1;i<=n;i++){ scanf("%lf",&(D[i].y)); D[i].x=1; } solve(); } return 0; }
