图像处理 -- 振铃现象

图像处理中，对一幅图像进行滤波处理，若选用的频域滤波器具有陡峭的变化，则会使滤波图像产生“振铃”，所谓“振铃”，就是指输出图像的灰度剧烈变化处产生的震荡，就好像钟被敲击后产生的空气震荡。如下图：

由卷积定理可将下面两种增强联系起来:

频域增强：

空域卷积：

其中f,g,h分别为输入图像，增强图像，空域滤波函数；F,G,H分别为各自的傅里叶变换。*为卷积符号。

在空间域将低通滤波作为卷积过程来理解的关键是h(x,y)的特性：可将h(x,y)分为两部分：原点处的中心部分，中心周围集中的成周期分布的外围部分。前者决定模糊，后者决定振铃现象。若外围部分有明显的震荡，则g(x,y)会出现振铃。利用傅里叶变换，我们发现，若频域滤波函数具有陡峭变化，则傅里叶逆变换得到的空域滤波函数会在外围出现震荡。

下面给出三个常用的低通滤波器：理想型、巴特沃斯型、高斯型。并分析他们对用的空域滤波函数的特点，验证上述结论。

理想型：

             

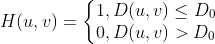
理想型滤波会出现振铃，可以看出空域滤波函数图像外围有剧烈震荡。

巴特沃斯型：

 

为阶数，1阶巴特沃斯没有“振铃“，随着阶数增大，振铃现象越发明显。下图取n=2,可以看出空域函数外围部分出现震荡。

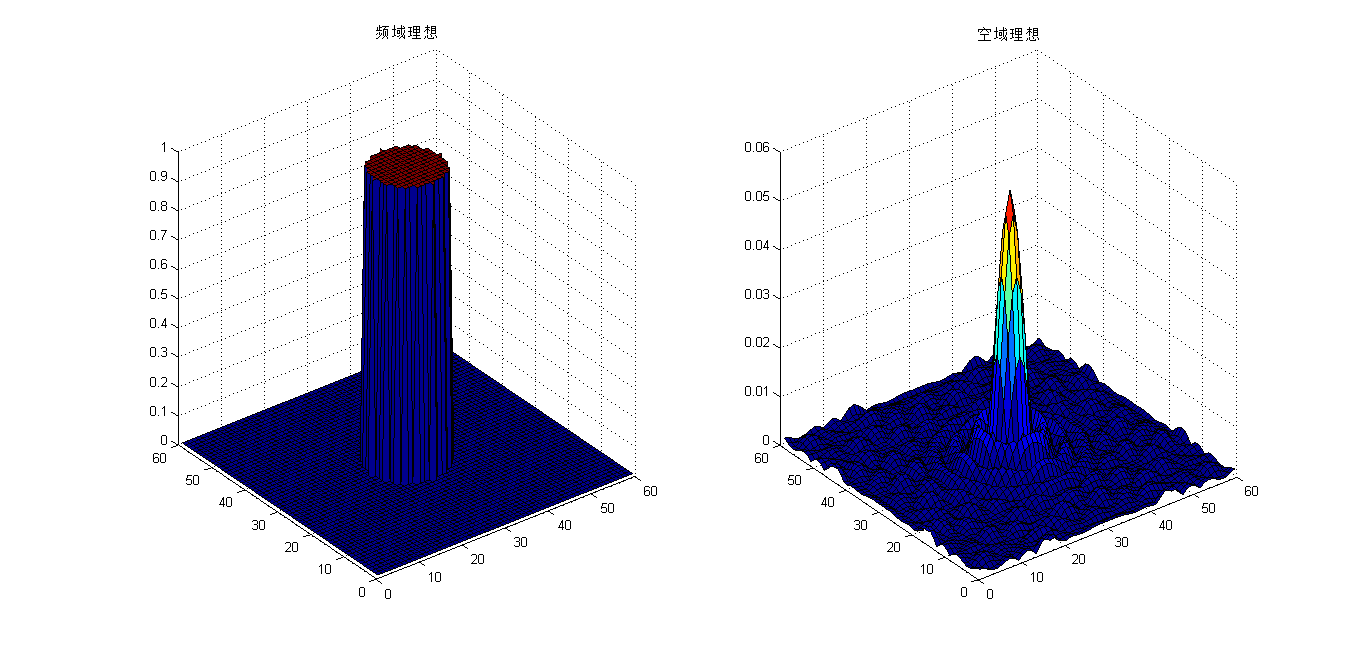
 高斯型：

          

高斯函数的傅里叶变换仍然是高斯函数，故高斯型滤波器不会产生“振铃“。

 上述图像的生成程序：

close all;
clear all;
d0=8;
M=60;N=60;
c1=floor(M/2);     
c2=floor(N/2);      
h1=zeros(M,N);      %理想型
h2=zeros(M,N);      %巴特沃斯型
h3=zeros(M,N);      %高斯型
sigma=4;
n=4;%巴特沃斯阶数
for i=1:M
    for j=1:N
        d=sqrt((i-c1)^2+(j-c2)^2);
        if d<=d0
            h1(i,j)=1;
        else
            h1(i,j)=0;
        end
        h2(i,j)=1/(1+(d/d0)^(2*n)); 
        h3(i,j)=exp(-d^2/(2*sigma^2)); 
    end
end
draw2(h1,'理想');
draw2(h2,'巴特沃斯');
draw2(h3,'高斯');
 
function draw2(h,name)
figure;
surf(h);title(strcat('频域',name));
fx=abs(ifft2(h));
fx=fftshift(fx);
figure;surf(fx);title(strcat('空域',name));

注：fftshift与ifftshift区别，对偶数行列矩阵相同，奇数相互弥补，组合使之可逆

https://blog.csdn.net/u010839382/article/details/41971603