PCA的核心思想:
削弱参数or特征向量之间的相关性,即消除信息冗余,找出一组完备基向量。
信息冗余的体现:
以二维坐标为例,y=x直线周围分布着许多点,我们只要知道了x,就能知道y,假设我们想知道的知识(x,y)的分布规律(在这里是呈线性的),而不是分布坐标,因此有一个维度是冗余的。
如何消除冗余?
y=x经过顺时针旋转45°,仍然是线性分布的,这时我们只需要一个横坐标即可,实现了降维。
也就是说,通过某种变换,如旋转变换,来实现降维or消除冗余or削弱相关性。
参考该链接:https://blog.csdn.net/baimafujinji/article/details/79376378
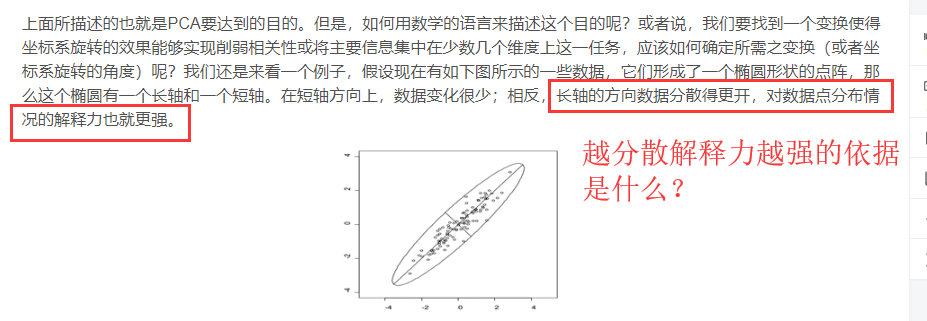
如上图所说,为什么越“分散”越有解释性?即为什么说直接求方差最大化即可?
直观上,PCA是对原数据进行投影变换,希望投影的点尽量分散。
从数学公式推导来解释:
【西瓜书230页推导】
考虑整个训练集,原样本点xi与基于投影重构的样本点xi'的距离最小化,可以得到协方差矩阵的项的相反数。