DSP

Hilbert 变换

Hilbert 变换可用于形成解析信号。解析信号在通信领域中很有用，尤其是在带通信号处理中。工具箱函数 hilbert 计算实数输入序列 x 的 Hilbert 变换，并返回相同长度的复数结果，即 y = hilbert(x)，其中 y 的实部是原始实数数据，虚部是实际 Hilbert 变换。在涉及到连续时间解析信号时，y 有时被称为解析信号。离散时间解析信号的关键属性是它的 Z 变换在单位圆的下半部分为 0。解析信号的许多应用都与此属性相关；例如，用解析信号避免带通采样操作的混叠效应。解析信号的幅值是原始信号的复包络。

Hilbert 变换对实际数据作 90 度相移；正弦变为余弦，反之亦然。要绘制一部分数据及其 Hilbert 变换，请使用

t = 0:1/1024:1;
x = sin(2*pi*60*t);
y = hilbert(x);

plot(t(1:50),real(y(1:50)))
hold on
plot(t(1:50),imag(y(1:50)))
hold off
axis([0 0.05 -1.1 2])
legend('Real Part','Imaginary Part')

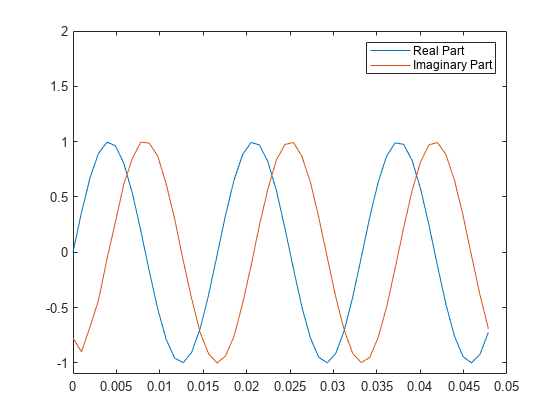
解析信号可用于计算时序的瞬时属性，即时序在任一时间点的属性。该过程要求信号是单分量的。

Hilbert 变换与瞬时频率

Hilbert 变换仅可估计单分量信号的瞬时频率。单分量信号在时频平面中用单一“脊”来描述。单分量信号包括单一正弦波信号和 chirp 等信号。

生成以 1 kHz 采样的时长为两秒的 chirp 信号。指定 chirp 信号的最初频率为 100 Hz，一秒后增加到 200 Hz。

fs = 1000;
t = 0:1/fs:2-1/fs;
y = chirp(t,100,1,200);

使用通过 pspectrum 函数实现的短时傅里叶变换来估计 chirp 信号的频谱图。下图中每个时间点有一个峰值频率，很好地描述了这一信号。

pspectrum(y,fs,'spectrogram')

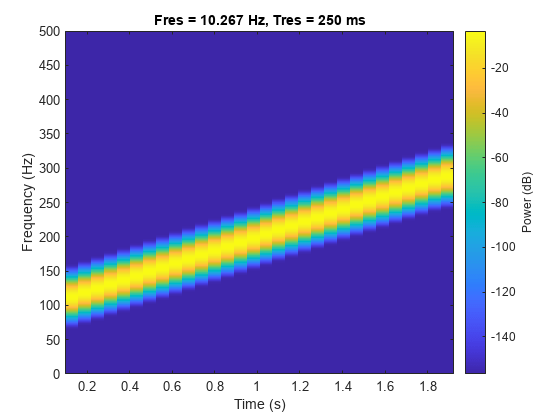
计算解析信号并对相位进行微分以得到瞬时频率。对导数进行缩放以得到有意义的估计。

z = hilbert(y);
instfrq = fs/(2*pi)*diff(unwrap(angle(z)));

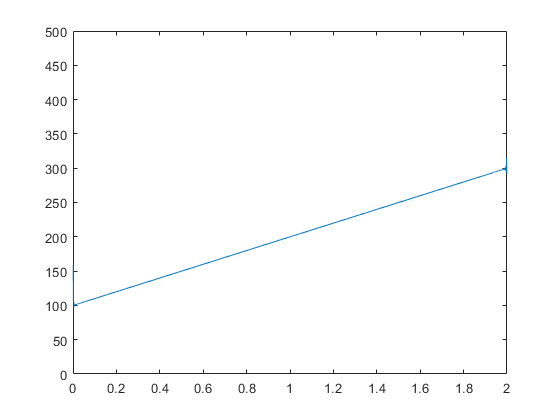
instfreq 函数只需一步即可计算并显示瞬时频率。

instfreq(y,fs,'Method','hilbert')

当信号不是单分量时，该方法会失败。

生成频率为 60 Hz 和 90 Hz 的两个正弦波的总和，以 1023 Hz 采样两秒。计算并绘制频谱图。在每个时间点都显示存在两个分量。

fs = 1023;
t = 0:1/fs:2-1/fs;
x = sin(2*pi*60*t)+sin(2*pi*90*t);

pspectrum(x,fs,'spectrogram')
yticks([60 90])

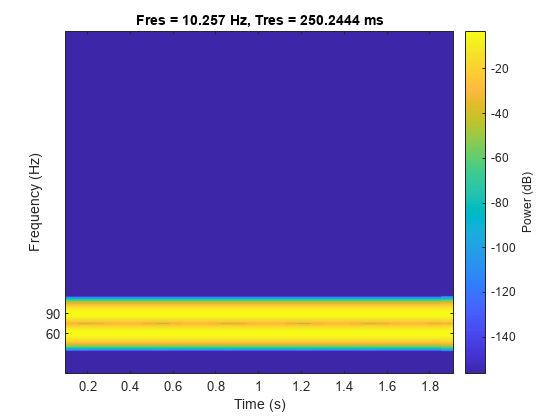
计算分析信号并对其相位求微分。放大包含正弦波频率的区域。分析信号预测瞬时频率，即正弦波频率的平均值。

z = hilbert(x);
instfrq = fs/(2*pi)*diff(unwrap(angle(z)));

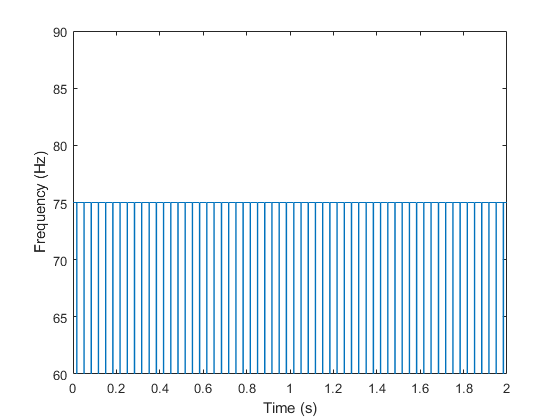
instfreq 函数也估算平均值。

instfreq(x,fs,'Method','hilbert')

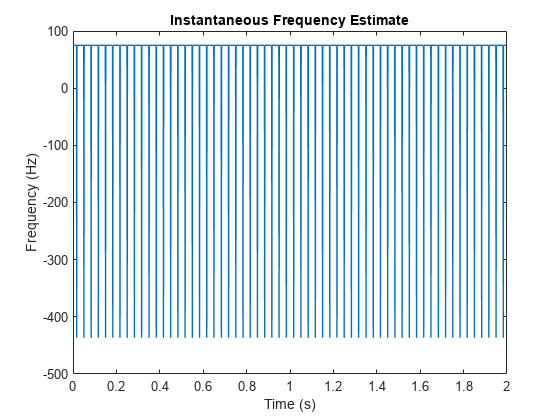
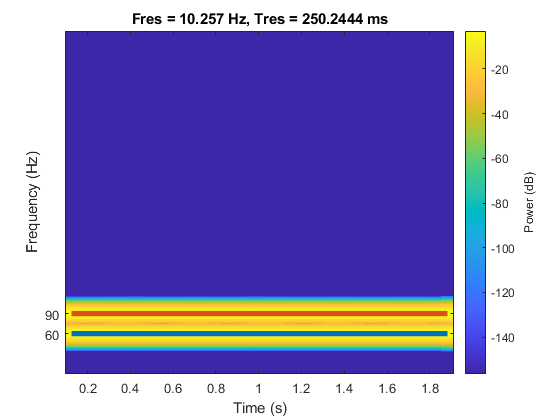
要采用时间的函数来估算这两个频率，请使用 spectrogram 求功率频谱密度，使用 tfridge 跟踪两个脊。在 tfridge 中，将更改频率的罚分指定为 0.1。

[s,f,tt] = pspectrum(x,fs,'spectrogram');

numcomp = 2;
[fridge,~,lr] = tfridge(s,f,0.1,'NumRidges',numcomp);

pspectrum(x,fs,'spectrogram')

Reference

　　1. MathWorks