Priority queue - 优先队列
相关概念
Priority queue优先队列是一种用来维护由一组元素构成的集合S的数据结构,
其中的每一种元素都有一个相关的值,称为关键字(key)。
一个最大有限队列支持一下操作:
insert(S,x):把元素x插入到集合S中.
maximum(S):返回集合S中具有最大关键字的元素.
extract_max(S):去掉并返回S中具有最大关键字的元素
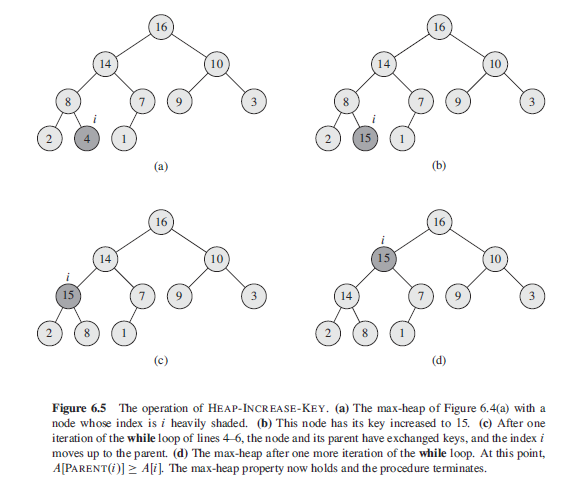
increase_key(S,x,k):将集合S中的元素x的关键字值增加到k,这里假设k的值不小于x元素原来的关键字的值
最大优先队列的应用有很多,其中一个就是在共享计算机系统的作业调度.最大优先队列记录将要执行的各个作业以及他们之间的相对优先级. 当一个作业完成或者被中断后,调度器调用extract_max(S),从所有作业中,选优具有最高优先级的作业来执行. 在任何时候,调度器都可以调用insert把一个新的作业加入到队列中.
相应地,最小优先队列支持的操作包括:insert,minimum,extract_min和decrease_key.最小优先队列可以被用于基于事件驱动的模拟器.队列中保存要模拟的事件,每个事件都有一个发生时间作为其关键字.
事件必须按照发生的时间顺序进行模拟,因为某一事件的模拟结果可能会触发其他事件的模拟. 在每一步,模拟程序调用extract_min来获得下一个要模拟的事件.当一个新事件产生时,模拟器通过调用insert将其插入到最小优先级队列中.
优先队列可以用堆来实现.对一个像作业调度或时间驱动模拟器这样的程序来说,优先队列的元素对应着应用程序中的对象.
Python programming # 优先队列是基于最大堆实现的. import heap_sorting # heap_sorting 模块代码位于: https://www.cnblogs.com/zzyzz/p/12869256.html def heap_maximum(A): return A[0] def heap_extract_max(A, heap_size): # heap_size 是堆的一个属性, 这里通过一个函数参数的形式实现. if heap_size < 1: print('error - heap underflow') return False max = A.pop(0) heap_size -= 1 heap_sorting.max_heapify(A,1,heap_size) return max if __name__ == '__main__': A = [16, 14, 10, 8, 7, 9, 3, 2, 4, 1] print('Before', A) heap_extract_max(A, 10) print('After', A) 结果打印: Before [16, 14, 10, 8, 7, 9, 3, 2, 4, 1] After [14, 10, 8, 7, 9, 3, 2, 4, 1]
def heap_increase_key(A, i, key): if key < A[i-1]: print('error - new key is smaller than current key') return False # 最大堆 A 中的第 i 个元素 A[i-1] 首先被替换成待插入的元素 key A[i-1] = key # 新插入的元素会不断地与其父结点进行比较, 如果当前元素 key 比较大, 则与其父结点进行交换, 更新 i 的值后继续比较. 直到当前元素 key 小于其父结点的时候终止循环. while i > 1 and A[heap_sorting.parent(i)-1] < A[i-1]: print(A[heap_sorting.parent(i) - 1], A[i - 1]) A[i-1], A[heap_sorting.parent(i)-1] = A[heap_sorting.parent(i)-1], A[i-1] i = heap_sorting.parent(i) print('i',i) print('A',A) if __name__ == '__main__': A = [16, 14, 10, 8, 7, 9, 3, 2, 4, 1] print('Before', A) heap_increase_key(A,9,15) # 将 15 插入到最大堆 A 中. 然后加工新的数组为新的最大堆. print('After', A)
结果打印: Before [16, 14, 10, 8, 7, 9, 3, 2, 4, 1] 8 15 # 第一次循环的 parent 和 key i 4 # parent < key, 更新 i A [16, 14, 10, 15, 7, 9, 3, 2, 8, 1] # 第一次循环后得到的新数组 14 15 # 第二次循环的 parent 和 key i 2 # parent < key, 更新 i A [16, 15, 10, 14, 7, 9, 3, 2, 8, 1] # # 第二次循环后得到的新数组 After [16, 15, 10, 14, 7, 9, 3, 2, 8, 1] # 循环退出后的得到新数组即为新的最大堆
def max_heap_insert(A, key, heap_size): heap_size += 1 A.insert(heap_size-1, -float('inf')) print(A) heap_increase_key(A, heap_size, key) if __name__ == '__main__': A = [16, 14, 10, 8, 7, 9, 3, 2, 4, 1] print('Before', A) max_heap_insert(A,13,10) print('After', A) 结果打印: Before [16, 14, 10, 8, 7, 9, 3, 2, 4, 1] [16, 14, 10, 8, 7, 9, 3, 2, 4, 1, -inf] # 先在对应的位置上设置一个 sentinel 7 13 # parent < key i 5 # 交换 parent 和 key 后更新 i A [16, 14, 10, 8, 13, 9, 3, 2, 4, 1, 7] # 交换后新的数组 After [16, 14, 10, 8, 13, 9, 3, 2, 4, 1, 7] # 循环退出后的结果
Reference,
1. Introduction to algorithms