【bzoj1787】[Ahoi2008]Meet 紧急集合

【解析】

三个点两两的lca一共有3个，其中两个一样的，那个不一样的就是集合点。

为什么是那个点呢？？？求助~

然后求三个点到集合点的距离。

今晚徐老大给我讲为什么那个点最优了，自己整理一下加深理解。

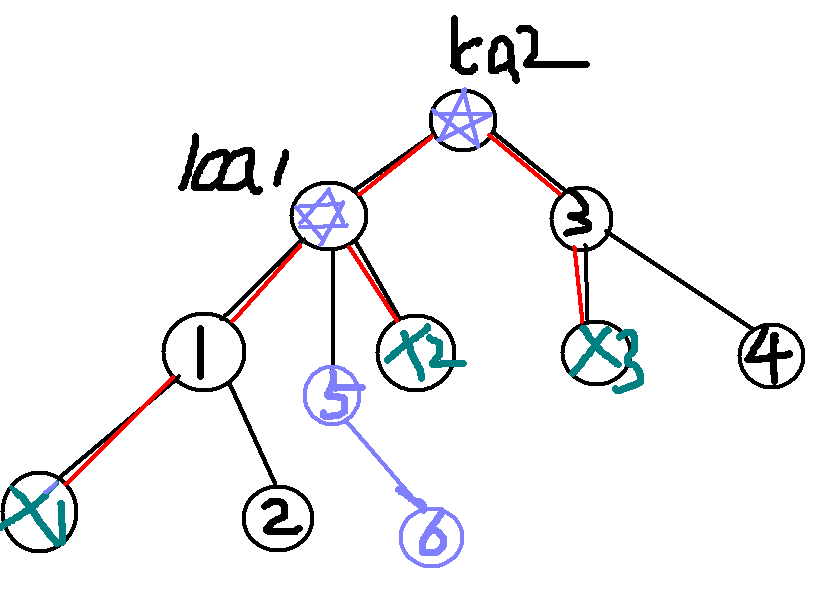
首先需要集合的三个点是x1,x2,x3,两两的lca为lca1，lca2，其中有两对重着，所以三个点两两求lca有两个。

我们可以得出几个结论：

（1）树上三个点两两求lca，所求的三个lca中两个是相同的。

（2）需要集合的点到他们三个lca中不同的那个lca集合最优。

首先我们先证明一下三个点到他们lca集合路径会最优（你先别管是哪个lca，反正是lca就对了）。

对于上图我们发现，走红色路径一定比不是红色路径的路径优。

①假设我们到结点编号为1的点集合，当集合点（也就是目前的编号为1的那个点）向靠近他们lca的方向移动时，（假设移向他爸爸，正好是lca1），那么跟之前的路径相比，

x2,x3比之前的路径长度各-1，x1比之前的路径长+1，两个点路径长-1，一个点路径长+1，显然与之前相比，向lca的方向移动，结果更优。

②假设集合点在结点4时，我们往靠近lca的方向移动，假设到结点3，发现x1,x2,x3的路径与原来相比-1，显然更能说明集合点往lca方向移动更优。

③假设x3在结点6，（这种情况是x1,x2,x3都在lca的子树中，说明三个点的两两lca相同），假设此时集合点为结点1，我们向靠近lca的方向移动，到lca1，此时

x2,x3的路径长-1，（注意此时x3已经在结点6了），x1的路径长+1，显然比集合点改变之前更优。

综上所述我们发现集合点在他们的lca路径最优。

反正三个点两两lca只有3个我们枚举一下在哪个lca时路径最优即可。

对于结论（2），两个相同的lca一定在不同的那个lca上面，也就是两个相同的lca比不同的那个lca深度浅。

为什么呢？因为一个点到它lca的路径是唯一的。（仍是原图中标号的x1,x2,x3）,lca1是x1,x2的lca，lca2是x2,x3的lca。

如果从x1向上冲，一定要先冲破他自己的lca1在冲向lca2，又因为lca1的深度深，相对于lca2少跑一层，所以在lca1最优，或者是

自己像刚才证明那样证明一下。

【代码】

#include<iostream>
#include<cstdio>
using namespace std;
#define N 500003
int sumedge,n,m,x,y,A,B,C,D,a,b,c,d,L;
int head[N],size[N],deep[N],dis[N],dad[N],top[N];
struct Edge
{
    int x,y,next;
    Edge(int x=0,int y=0,int next=0):x(x),y(y),next(next){}
}edge[N<<1];
inline int read()//读入优化 
{
    int x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
inline void add_edge(int x,int y)//加边 
{
    edge[++sumedge]=Edge(x,y,head[x]);
    head[x]=sumedge;
}
inline void dfs(int x)//树剖求lca 
{
    size[x]=1;
    deep[x]=deep[dad[x]]+1;
    for(int i=head[x];i;i=edge[i].next)
    {
        if(dad[x]!=edge[i].y)
        {
            dad[edge[i].y]=x;
            dis[edge[i].y]=dis[x]+1;
            dfs(edge[i].y);
            size[x]+=size[edge[i].y];
        }
    }
}
inline void dfs1(int x)//树剖求lca 
{
    int s=0;
    if(!top[x])top[x]=x;
    for(int i=head[x];i;i=edge[i].next)
    {
        if(dad[x]!=edge[i].y&&size[edge[i].y]>size[s])
        {
            s=edge[i].y;
        }
    }
    if(s)
    {
        top[s]=top[x];
        dfs1(s);
    }
    for(int i=head[x];i;i=edge[i].next)
    {
        if(dad[x]!=edge[i].y&&edge[i].y!=s)
        dfs1(edge[i].y);
    }
}
inline int lca(int x,int y)//树剖求Lca 
{
    for(;top[x]!=top[y];)
    {
        if(deep[top[x]]>deep[top[y]])
        swap(x,y);
        y=dad[top[y]];
    }
    if(deep[x]>deep[y])
    swap(x,y);
    return x;
}
inline int l(int x,int y)//树上两点之间的最短路径 两个点到跟的路径长度减去两倍的lca到根的长度。  
{
    return dis[x]+dis[y]-2*dis[lca(x,y)];
}
int main()
{
    n=read();m=read();//n个点 m个询问
    for(int i=1;i<n;i++)
    {
        x=read();y=read();
        add_edge(x,y);//加边 
        add_edge(y,x);
    }
    dfs(1);//树剖求lca的dfs 
    dfs1(1);
    for(int i=1;i<=m;i++)
    {
        a=read();b=read();c=read();
        A=lca(a,b);B=lca(a,c);C=lca(b,c);
        D=A^B^C;//三个lca中有两个相同的 D是那个不同的 
        L=l(a,D)+l(b,D)+l(c,D);//三点到D的距离 用树上两点之间的最短路径做。 
        printf("%d %d
",D,L);
    }
    return 0;
}

//不知道为什么同学用的树剖和vector数组存边一直re。。。。然后写上读入优化就过了？？？还好我用的邻接表~

【bzoj1787】[Ahoi2008]Meet 紧急集合

Description

Input

Output

Sample Input

Sample Input

HINT