集合的划分
【问题描述】
设S是一个具有n个元素的集合,S={a1,a2,……,an},现将S划分成k个满足下列条件的子集合S1,S2,……,Sk ,且满足:
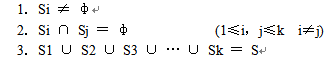
则称S1,S2,……,Sk是集合S的一个划分。它相当于把S集合中的n个元素a1 ,a2,……,an 放入k个(0<k≤n<30=无标号的盒子中,使得没有一个盒子为空。请你确定n个元素a1 ,a2 ,……,an 放入k个无标号盒子中去的划分数S(n,k)。
【输入样例】setsub.in
23 7
【输出样例】setsub.out
4382641999117305
代码如下:
#include<iostream>
#include<cstdio>
#include<cstdlib>
using namespace std;
int hf(int n,int k)
{
if(n<k||k==0)return 0;
if(n==k||k==1)return 1;
return hf(n-1,k)*k+hf(n-1,k-1);
}
void write(long long x)
{
if(!x)return;
write(x/10);
putchar(x%10+'0');
}
int main()
{
int n,k;
scanf("%d%d",&n,&k);
write(hf(n,k));
return 0;
}
分析:
两种情况:
1、{an}是k个子集中的一个,于是我们只要把a1,a2,……,an-1 划分为k-1子集,便解决了本题,这种情况下的划分数共有S(n-1,k-1)个;
2、{an}不是k个子集中的一个,则an必与其它的元素构成一个子集。则问题相当于先把a1,a2,……,an-1 划分成k个子集,这种情况下划分数共有S(n-1,k)个;然后再把元素an加入到k个子集中的任一个中去,共有k种加入方式,这样对于an的每一种加入方式,都可以使集合划分为k个子集,因此根据乘法原理,划分数共有k * S(n-1,k)个。
w因此,我们可以得出划分数S(n,k)的递归关系式为:
w S(n,k)=S(n-1,k-1) + k * S(n-1,k) (n>k,k>0)
w S(n,k)=0 (n<k)或(k=0)
w S(n,k)=1 (k=1)或(k=n)