Manthan, Codefest 16 D. Fibonacci-ish

D. Fibonacci-ish

time limit per test

3 seconds

memory limit per test

512 megabytes

input

standard input

output

standard output

Yash has recently learnt about the Fibonacci sequence and is very excited about it. He calls a sequence Fibonacci-ish if

1. the sequence consists of at least two elements
2. f0 and f1 are arbitrary
3. fn + 2 = fn + 1 + fn for all n ≥ 0.

You are given some sequence of integers a1, a2, ..., an. Your task is rearrange elements of this sequence in such a way that its longest possible prefix is Fibonacci-ish sequence.

Input

The first line of the input contains a single integer n (2 ≤ n ≤ 1000) — the length of the sequence ai.

The second line contains n integers a1, a2, ..., an (|ai| ≤ 109).

Output

Print the length of the longest possible Fibonacci-ish prefix of the given sequence after rearrangement.

Examples

input

3
1 2 -1

output

3

input

5
28 35 7 14 21

output

4

Note

In the first sample, if we rearrange elements of the sequence as  - 1, 2, 1, the whole sequence ai would be Fibonacci-ish.

In the second sample, the optimal way to rearrange elements is 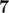, , , , 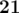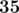28.

思路：直接暴力枚举前两个元素，然后先离散化下，并用map一一对应下数值，开个数组记录各个值的个数，然后根据斐波那契数列依次推下个数字

在数组中查找，其中开始为0，0需要特判否则复杂度n³；

#include<stdio.h>
#include<algorithm>
#include<iostream>
#include<string.h>
#include<math.h>
#include<queue>
#include<map>
using namespace std;
const long long N=1e9+7;
typedef long long LL;
LL vv[25];
LL MM[1005];
int NN[1005];
int KK[1005];
map<LL,LL>my;
LL quickmi(long long  a,long long  b);
int main(void)
{
    int i,j,k;
    while(scanf("%d",&k)!=EOF)
    {memset(NN,0,sizeof(NN));
        for(i=0; i<k; i++)
        {
            scanf("%I64d",&MM[i]);
        }
        int cnt=1;sort(MM,MM+k);my[MM[0]]=1;
        NN[1]++;
        for(i=1; i<k; i++)
        {
            if(MM[i]!=MM[i-1])
                cnt++;
            NN[cnt]++;
            my[MM[i]]=cnt;
        }int maxx=2;
        for(i=0; i<k; i++)
        {
            for(j=0; j<k; j++)
            {int sum=2;
                if(i!=j)
                {int KK[1005]={0};LL p=MM[i];LL q=MM[j];
                if(p==0&&q==0)
                {
                    sum=NN[my[0]];
                }
                else {KK[my[p]]++;KK[my[q]]++;
                 while(true)
                 {
                     LL ans=p+q;
                     KK[my[ans]]++;
                     if(KK[my[ans]]<=NN[my[ans]])
                     sum++;
                     else break;
                     p=q;q=ans;
                 }}
                 if(sum>maxx)
                    maxx=sum;}
            }
        }printf("%d
",maxx);
    }
    return 0;
}

LL quickmi(long long  a,long long  b)
{
    LL sum=1;
    while(b)
    {
        if(b&1)
            sum=(sum*a)%(N);
        a=(a*a)%N;
        b/=2;
    }
    return sum;
}