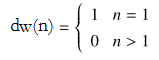《积性函数求和的几种方法》这篇paper大概就是讲了杜教筛和任之州一种神奇的自创做法。%%%IOI爷
分别复杂度是O(n^(2/3))和O(n^(3/4)/logn)的。
在一般情况下,后者的常数和复杂度都更加优秀。
这篇就先讲杜教筛好了
①杜教筛
运用Dircichlet卷积来完成复杂度的化简。
可以参考唐教的介绍 http://blog.csdn.net/skywalkert/article/details/50500009
还是上几个例题。
A. 求n个正整数的约数之和,其中n<=10^12。
运用莫比乌斯反演的那个技巧即可做到O(sqrt(n))的复杂度。
其实这跟杜教筛并没有什么关系…
#include <iostream> #include <stdio.h> #include <stdlib.h> #include <algorithm> #include <string.h> #include <vector> #include <math.h> #include <limits> #include <set> #include <map> using namespace std; long long n; int main() { cin>>n; long long ed=1,ans=0; for(long long a=1;a<=n;a=ed+1) { ed=(n/(n/a)); ans+=(a+ed)*(ed-a+1)/2*(n/a); } cout<<ans; }
B. 求前n个正整数的欧拉函数之和,其中n<=10^11。
我们运用主定理进行分析:
根据唐教说只要展开一层就行了.
最后一步可以直接根据积分得到(symbolab)。
如果我们用筛法处理前k个前缀和,那么复杂度就变成了O($frac{n}{sqrt{k}}$),当k=$n^frac{2}{3}$时可以取到极值。
为什么我们会这么考虑呢?
因为Dircichlet卷积:
例如我们知道莫比乌斯反演
设$id(n)=n$,我们知道$varphi(i)*I=id$。
那总结一下如果Dircichlet卷积的左边其中一个函数是待求前缀和的,而且卷积的另外两个函数比较好计算前缀和,那么就可以简化计算的过程。
51nod 1239
实现的时候要注意一些细节
由于常数问题比较严重,还是建议用map稍微记忆化意思意思
upd on 2017-02-01:
这篇文章有一些年头了...这里说一下这个map其实是可以不用的...
注意到每个参数都是n的约数,有一个储存上的trick,大致如下:
其中s大约为$sqrt{n}$。这样储存就少了一个log了(洲阁筛也需要这个trick,但是实际运行速度好像相差不大)
#include <iostream> #include <stdio.h> #include <stdlib.h> #include <algorithm> #include <string.h> #include <vector> #include <math.h> #include <limits> #include <set> #include <map> using namespace std; typedef long long ll; ll MOD=1000000007; #define MM 5000000 int ps[MM+5],pn=0,mu[MM+5],eul[MM+5]; bool np[MM+5]; ll qzheul[MM+5]; void shai() { np[1]=mu[1]=eul[1]=1; for(int i=2;i<=MM;i++) { if(!np[i]) {mu[i]=-1; ps[++pn]=i; eul[i]=i-1;} for(int j=1;j<=pn&&i*ps[j]<=MM;j++) { np[i*ps[j]]=1; if(i%ps[j]) { mu[i*ps[j]]=-mu[i]; eul[i*ps[j]]=eul[i]*(ps[j]-1); } else { mu[i*ps[j]]=0; eul[i*ps[j]]=eul[i]*ps[j]; break; } } } for(int i=1;i<=MM;i++) qzheul[i]=(qzheul[i-1]+eul[i])%MOD; } ll qp(ll a,ll b) { if(b==0) return 1; ll hf=qp(a,b>>1); hf=hf*hf%MOD; if(b&1) hf=hf*(a%MOD)%MOD; return hf; } ll rv2=qp(2,MOD-2),n; #define G 233333 ll p1[G],p2[G]; ll &gm(ll x) { if(x<G) return p1[x]; return p2[n/x]; } ll eulsum(ll x) { if(x<=MM) return qzheul[x]; ll &ps=gm(x); if(ps!=-1) return ps; ll ans,lst; if(x%MOD!=0) ans=(x%MOD)*((x%MOD)+1)%MOD*rv2%MOD; else ans=0; for(ll p=2;p<=x;p=lst+1) { lst=x/(x/p); ans-=((lst-p+1)%MOD)*eulsum(x/p)%MOD; ans%=MOD; } ans=(ans%MOD+MOD)%MOD; return ps=ans; } int main() { memset(p1,-1,sizeof(p1)); memset(p2,-1,sizeof(p2)); shai(); cin>>n; cout<<eulsum(n)<<" "; }
C. 求前n个正整数的mu函数(莫比乌斯函数)之和,n<=10^11。
咦好像$sum_{d|n}mu(d)=[n=1]$ 
我们来手推一发
$1={sum_{i=1}^nsum_{d|i}mu(d)}={sum_{d=1}^nmu(d)*lfloorfrac{n}{d} floor}={sum_{d=1}^nmu(d)*sum_{i=1}^{lfloorfrac{n}{d} floor}1}=sum_{i=1}^{n}sum_{d=1}^{lfloorfrac{n}{i} floor}mu(d)$
(latex打得好辛苦啊QAQ
所以也可以用同样的方法搞搞
51nod 1244
#include <iostream> #include <stdio.h> #include <stdlib.h> #include <algorithm> #include <string.h> #include <vector> #include <math.h> #include <limits> #include <set> #include <map> using namespace std; typedef long long ll; ll MOD=1000000007; #define MM 6000000 int ps[MM+5],pn=0,mu[MM+5]; bool np[MM+5]; ll qzhmu[MM+5]; void shai() { np[1]=mu[1]=1; for(int i=2;i<=MM;i++) { if(!np[i]) {mu[i]=-1; ps[++pn]=i;} for(int j=1;j<=pn&&i*ps[j]<=MM;j++) { np[i*ps[j]]=1; if(i%ps[j]) mu[i*ps[j]]=-mu[i]; else{mu[i*ps[j]]=0; break;} } } for(int i=1;i<=MM;i++) qzhmu[i]=qzhmu[i-1]+mu[i]; } #define G 233333 ll p1[G],p2[G],n; ll &gm(ll x) { if(x<G) return p1[x]; return p2[n/x]; } ll musum_(ll x) { if(x<=MM) return qzhmu[x]; ll &ps=gm(x); if(ps!=p2[0]) return ps; ll ans=1,lst; for(ll p=2;p<=x;p=lst+1) { lst=x/(x/p); ans-=(lst-p+1)*musum_(x/p); } return ps=ans; } ll musum(ll x) { memset(p1,-2333,sizeof(p1)); memset(p2,-2333,sizeof(p2)); n=x; return musum_(x); } int main() { shai(); ll a,b; cin>>a>>b; cout<<musum(b)-musum(a-1)<<" "; }
还有唐教博客上的一些例题也顺带做了一下
bzoj3944 双倍经验,略
hdu5608
还是杜教筛搞搞。
设g(n)=n^2-3n+2
容易得到f*1=g。
则$sum_{i=1}^ng(i)=sum_{i=1}^nsum_{d=1}^{lfloorfrac{n}{i} floor}f(d)$。(推导和上面一样)
而$sum_{i=1}^ng(i)=frac{n(n+1)(2n+1)}{6}-frac{3n(n+1)}{2}+2n=frac{n(n-1)(n-2)}{3}$。
初始化的时候我们可以先线筛,然后莫比乌斯反演一下暴力更新。
$f(n)=sum_{d|n}{mu(frac{n}{d})g(d)}$
对于每一个g暴力更新它的倍数,由调和级数显然是O(plogp)的(假设你预处理到p
这种题出到bc div2简直了
#include <iostream> #include <stdio.h> #include <stdlib.h> #include <algorithm> #include <string.h> #include <vector> #include <math.h> #include <limits> #include <set> #include <map> using namespace std; typedef long long ll; ll MOD=1000000007; #define MM 600000 int ps[MM/5],pn=0,mu[MM+5]; bool np[MM+5]; ll smf[MM+5],fqzh[MM+5]; void shai() { np[1]=mu[1]=1; for(int i=2;i<=MM;i++) { if(!np[i]) {mu[i]=-1; ps[++pn]=i;} for(int j=1;j<=pn&&i*ps[j]<=MM;j++) { np[i*ps[j]]=1; if(i%ps[j]) mu[i*ps[j]]=-mu[i]; else {mu[i*ps[j]]=0; break;} } } for(int d=1;d<=MM;d++) { ll g=((ll)d*d%MOD-3*d%MOD+2)%MOD; for(int n=d;n<=MM;n+=d) smf[n]=(smf[n]+mu[n/d]*g%MOD)%MOD; } for(int i=1;i<=MM;i++) fqzh[i]=(fqzh[i-1]+smf[i])%MOD; } ll qp(ll a,ll b) { if(b==0) return 1; ll hf=qp(a,b>>1); hf=hf*hf%MOD; if(b&1) hf=hf*(a%MOD)%MOD; return hf; } ll rv3=qp(3,MOD-2); #define G 23333 ll p1[G],p2[G],n; ll &gm(ll x) { if(x<G) return p1[x]; return p2[n/x]; } ll gf(ll x) { if(x<=MM) return fqzh[x]; ll &ps=gm(x); if(ps!=p2[0]) return ps; ll lst,ans=x*(x-1)%MOD*(x-2)%MOD*rv3%MOD; for(ll p=2;p<=x;p=lst+1) { lst=x/(x/p); ans=ans-(lst-p+1)*gf(x/p)%MOD; ans%=MOD; } ans=(ans%MOD+MOD)%MOD; return ps=ans; } ll fs(ll x) { memset(p1,-2333,sizeof(p1)); memset(p2,-2333,sizeof(p2)); n=x; return gf(x); } int main() { shai(); int T,n; scanf("%d",&T); while(T--) { scanf("%d",&n); ll ans=fs(n); printf("%d ",int((ans%MOD+MOD)%MOD)); } }
2017-02-01:所有代码已经去掉了map= =

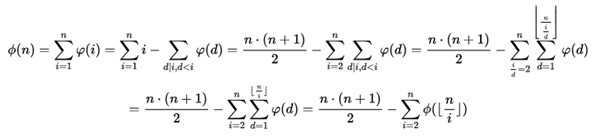
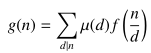
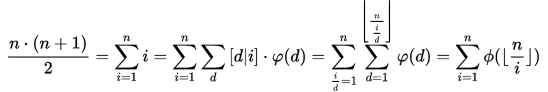
![KVR$M]RNG`~DNWXE@YXPALS KVR$M]RNG`~DNWXE@YXPALS](https://images2015.cnblogs.com/blog/903652/201702/903652-20170201140223339-214536702.png)