向量叉乘的线性性质 几何解释

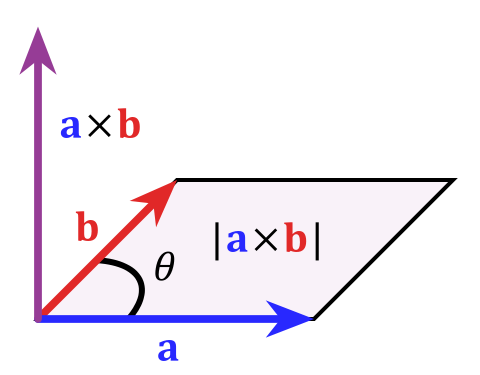
叉乘(向量的外积)是物理里面常常用到的概念, 它是由两个向量得到一个新的向量的运算。一般我们都是从几何意义下手: 向量(vec a)和(vec b)叉乘, 得到一个垂直于(vec a)和(vec b)的向量(vec a imes vec b), 它的方向由右手螺旋法则确定, 它的长度是(vec a)和(vec b)张开的平行四边形的面积:

[| vec a imes vec b | = |vec a| cdot |vec b| cdot sin heta ]

其中( heta)是(vec a)和(vec b)的夹角.

叉乘满足的基本的性质如下:

1. (vec a imes vec a = vec0), 因为夹角是0, 所以平行四边形面积也是0, 即叉积长度为0
2. (vec a imes vec b = - (vec b imes vec a)), 等式两边的叉积等大反向, 模长因为平行四边形不变而相同, 方向因为右手法则旋转方向相反而相反
3. ((lambda vec a) imes b = lambda (vec a imes vec b)), 这点比较好想, 因为: ①正数(lambda)数量乘不会影响(vec a)的方向, 所以左右的叉积方向一样; 负数(lambda)使得(vec a)反向了, 但也使得左右叉积方向相反. ②对(vec a)进行缩放, 平行四边形面积也同等缩放.
4. ((vec a+vec b) imes vec c = vec a imes vec c + vec b imes vec c), 这种分配率是以前最难想象的了.

上述3. 4.两点结合起来, 说明叉乘具有一种线性性质, 再结合2.就是双线性了(同时对左右具有线性性质). 一直以来我都想找到性质4. 的一种几何证明, 可它就像一个过不去的坎, 挡住了我追求完美的心.

每次想到性质4., 都会去想象空间中一点出发的三个随机向量, 然后又叉乘出两个新向量, 一共5个向量, 甚至画图都很难. 这个问题一直持续了很久, 后来某天突然想到, 可以固定一个向量, 剩余的工作在二维投影面完成啊~

结论4的证明

这里证明4.的等价结论: (vec a imes (vec b + vec c) = vec a imes vec b + vec a imes vec c). 如下图所示, 把向量(vec b)和(vec c)按照向量(vec a)的负方向, 投影到与(vec a)垂直的平面S.

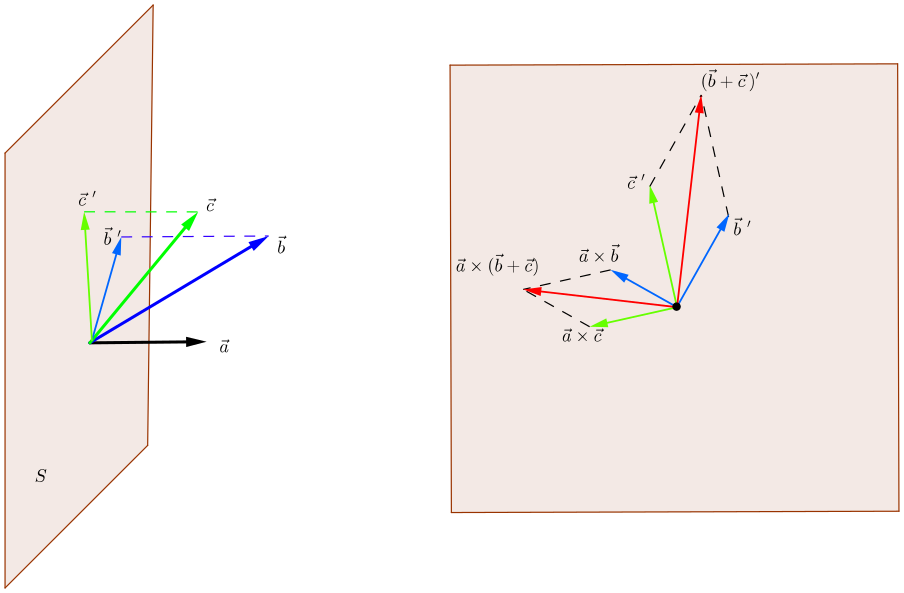
这里先要说明, 向量(vec a)和(vec b)的叉乘, 等于和(vec b)的投影(vec b \,')的叉乘:

[vec a imes vec b = vec a imes vec b \, ' ]

这个结论很好想象, 这种投影其实是把(vec b)掰成与(vec a)垂直的等价部分: 叉乘方向不会变, 并且平行四边形面积不变(底乘高,高没变).

那么这就好说了, 直接在投影面分析:

1. (vec a imes vec b)就是(vec b \,')逆时针旋转90度, 并且伸缩(|vec a|)(蓝色的向量)
2. (vec a imes vec c)就是(vec c\,')逆时针旋转90度, 并且伸缩(|vec a|)(绿色的向量)
3. (vec a imes (vec b +vec c)​)就是(vec b\,'+vec c\,'​)逆时针旋转90度, 并且伸缩(|vec a|​)(红色的向量)

换句话说, 两个平行四边形是相似的. 在左边那个平行四边形里, 我们得到了结论

[vec a imes (vec b + vec c) = vec a imes vec b + vec a imes vec b. ]

几何证明以后...

所有性质得到几何理解以后, 就感觉整个理论都通畅很多呢...

比如就可以分析, 解析几何下怎么计算叉乘:

[{egin{aligned}mathbf {u} imes mathbf {v} ={}&(u_{1}mathbf {i} +u_{2}mathbf {j} +u_{3}mathbf {k} ) imes (v_{1}mathbf {i} +v_{2}mathbf {j} +v_{3}mathbf {k} )\={}&u_{1}v_{1}(mathbf {i} imes mathbf {i} )+u_{1}v_{2}(mathbf {i} imes mathbf {j} )+u_{1}v_{3}(mathbf {i} imes mathbf {k} )+{}\&u_{2}v_{1}(mathbf {j} imes mathbf {i} )+u_{2}v_{2}(mathbf {j} imes mathbf {j} )+u_{2}v_{3}(mathbf {j} imes mathbf {k} )+{}\&u_{3}v_{1}(mathbf {k} imes mathbf {i} )+u_{3}v_{2}(mathbf {k} imes mathbf {j} )+u_{3}v_{3}(mathbf {k} imes mathbf {k} )\end{aligned}} ]

就是说, 利用前面的分配率, 我们就能够将坐标形式的叉乘归结为基底的叉乘! 对于基底, 我们按照最开始的叉乘定义可以求出他们的值(右手坐标系下):

[mathbf {i} imes mathbf {i} =mathbf {j} imes mathbf {j} =mathbf {k} imes mathbf {k} =mathbf {0} ]

[left{ {displaystyle {egin{aligned}mathbf {i} imes mathbf {j} &=mathbf {k} \mathbf {j} imes mathbf {k} &=mathbf {i} \mathbf {k} imes mathbf {i} &=mathbf {j} end{aligned}}} ight. quadquad left{ {displaystyle {egin{aligned}mathbf {j imes i} &=-mathbf {k} \mathbf {k imes j} &=-mathbf {i} \mathbf {i imes k} &=-mathbf {j} end{aligned}}} ight. ]

最后就是熟悉的形式:

[{displaystyle {egin{aligned} mathbf {u imes v} &=(u_{2}v_{3}-u_{3}v_{2})mathbf {i} +(u_{3}v_{1}-u_{1}v_{3})mathbf {j} +(u_{1}v_{2}-u_{2}v_{1})mathbf {k} \ &={egin{vmatrix}u_{2}&u_{3}\v_{2}&v_{3}end{vmatrix}}mathbf {i} -{egin{vmatrix}u_{1}&u_{3}\v_{1}&v_{3}end{vmatrix}}mathbf {j} +{egin{vmatrix}u_{1}&u_{2}\v_{1}&v_{2}end{vmatrix}}mathbf {k} \ &={egin{vmatrix}mathbf {i} &mathbf {j} &mathbf {k} \u_{1}&u_{2}&u_{3}\v_{1}&v_{2}&v_{3}\end{vmatrix}} end{aligned}}} ]

这里再放一张维基百科的图:

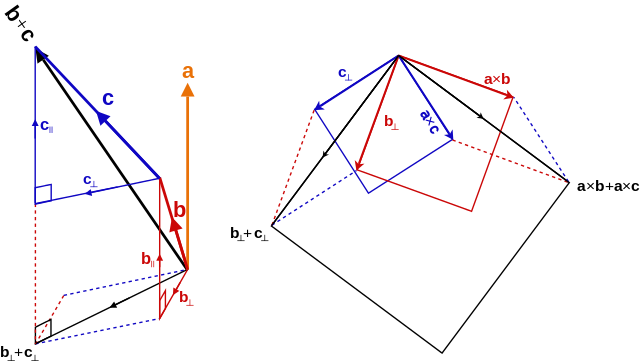
维基百科里还有更多性质的介绍和证明:

https://en.wikipedia.org/wiki/Cross_product