算法初探

更新记录

【1】2020.08.08-17:59

• 1.完善内容

正文

在一些特殊的问题中，例如在一有向有环图中求最长路径，点（边）可以重复经过，但是点权（边权）只算一次
（要是无限算不沿着环瞎就就彳亍嘛）
容易想到，在遇到环的时候我们要将这个环走一遍以获取最大值

那么缩点就是将环缩成一个点，然后进行DAG上的动态规划

我们回想强连通分量的定义：

在有向图G中，如果两个点u，ｖ间有一条从ｕ到ｖ的有向路径，同时还有一条从ｖ到ｕ的有向路径，则称两个点强连通
如果有向图G的每两个点都强连通，称G是一个强连通图
有向非强连通图的极大强连通子图，称为强连通分量。

也就是说强连通分量一定是一个环

这样我们第一步就通过tarjan算法找到强连通分量就可以

(dfn)代表搜索的(dfs)序
(low)代表在栈中所能追溯到的最小（早）的(dfs)序

那么这个栈是干啥呢，让我们按算法的顺序一步一步来

[算法开始]

遍历每个点的出边对应的点，如果没有搜索过就先搜索出边所对应的点
搜索后，记最小的(low)

如果搜索过且在栈中，就说明这两个点可以互相到达，记最小的(low)

如果其(dfs)序和(low)相等，就说明遍历完毕，并且这个点不能从其他的地方走过来
此时栈中的(n)上面的点（包括(n)）就是一个强连通分量

出栈，统计

inline void tarjan(int n){
	dfn[n]=++time;
	low[n]=time;
	stk[++stks]=n;
	for(int i=head[n];i;i=e[i].na){
		if(!dfn[e[i].np]){
			tarjan(e[i].np);
			low[n]=min(low[n],low[e[i].np]);
		}
		else if(!vis[e[i].np])
			low[n]=min(low[n],dfn[e[i].np]);
	}
	if(dfn[n]==low[n]){
		vis[n]=++tot;
		while(stk[stks]!=n){
			stnum[tot]+=1;
			vis[stk[stks]]=tot;
			stks-=1;
		}
		stnum[tot]+=1;
		stks-=1;
	}
}

【模板】缩点

将环缩为点之后重建图

此时的图是一个有向无环图

拓扑排序跑一个DAG上的dp就好

缩点之前

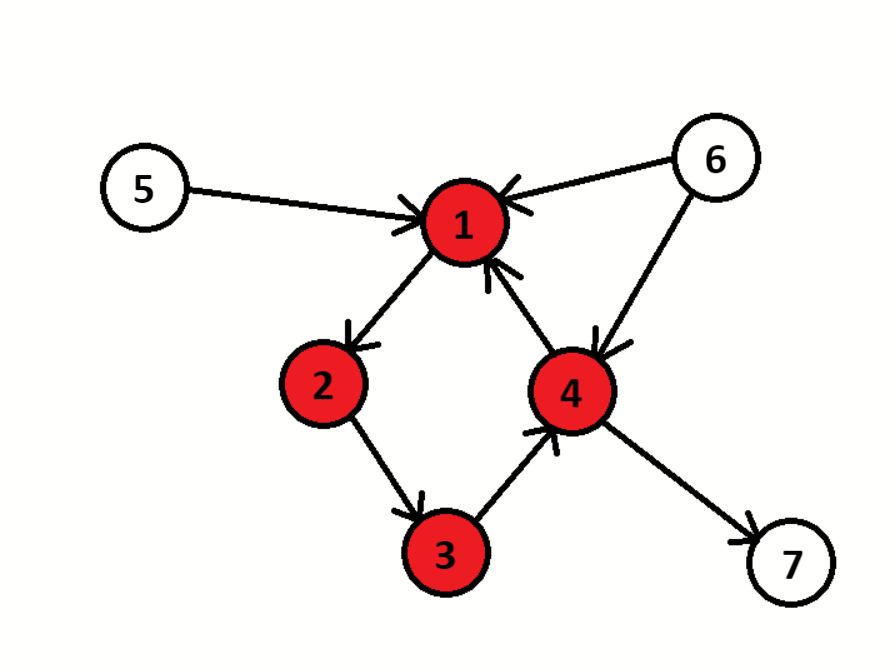
缩点之后

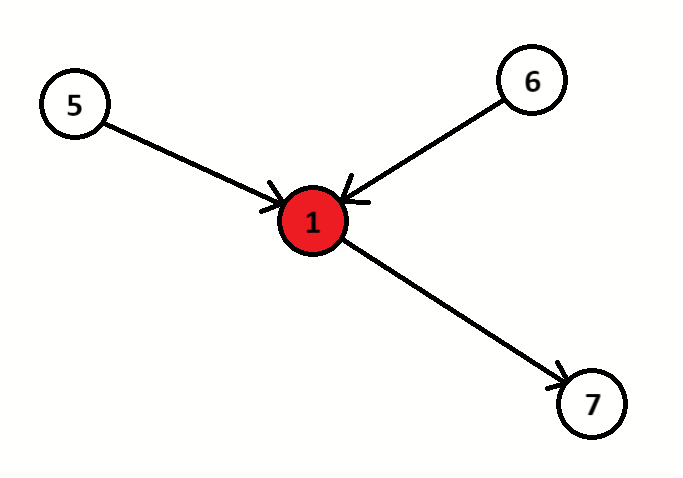
#include<iostream>
#include<queue>
#include<cstring>
#define N 200001
using namespace std;
struct Edge{
	int na,np;
}e[N],dag[N];
int head[N],head2[N],num2,num,now,n,m,fr,to,w[N],vis[N],dfn[N],lian[N],ru[N],low[N],times,stnum[N],stk[N],stks,maxn;
queue<int>q;
inline void add(int f,int t){
	e[++num].na=head[f];
	e[num].np=t;
	head[f]=num;
}
inline void add2(int f,int t){
	dag[++num2].na=head2[f];
	dag[num2].np=t;
	head2[f]=num2;
}
inline void tarjan(int n){
	dfn[n]=++times;
	low[n]=times;
	stk[++stks]=n;
	for(int i=head[n];i;i=e[i].na){
		if(!dfn[e[i].np]){
			tarjan(e[i].np);
			low[n]=min(low[n],low[e[i].np]);
		}
		else if(!vis[e[i].np]){
			low[n]=min(low[n],dfn[e[i].np]);
		}
	}
	if(dfn[n]==low[n]){
		vis[n]=n;
		while(stk[stks]!=n){
			stnum[n]+=w[stk[stks]];
			vis[stk[stks]]=n;
			stks-=1;
		}
		stnum[n]+=w[stk[stks]];
		stks-=1;
	}
}
int main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++) cin>>w[i];
	for(int i=1;i<=m;i++){
		cin>>fr>>to;
		add(fr,to);
	}
	for(int i=1;i<=n;i++){
		if(!dfn[i]) tarjan(i);
	}
	for(int i=1;i<=n;i++){
		for(int o=head[i];o;o=e[o].na){
			if(vis[i]!=i&&vis[e[o].np]!=e[o].np) continue;
			if(vis[i]==vis[e[o].np]) continue;
			add2(vis[i],vis[e[o].np]);
			ru[vis[e[o].np]]+=1;
		}
	}
	for(int i=1;i<=n;i++){
		if(!ru[i]){
			q.push(i),lian[i]=stnum[i];
			maxn=max(maxn,stnum[i]);
		}
	}
	while(q.size()){
		now=q.front();
		q.pop();
		for(int i=head2[now];i;i=dag[i].na){
			ru[dag[i].np]-=1;
			lian[dag[i].np]=max(lian[dag[i].np],lian[now]+stnum[dag[i].np]);
			maxn=max(maxn,lian[dag[i].np]);
			if(!ru[dag[i].np]){
				q.push(dag[i].np);
			}
		}
	}
	cout<<maxn;
}

[USACO03FALL][HAOI2006]受欢迎的牛 G

首先读题，整理信息可知：

• 环上的牛互相喜欢
• 能被所有牛喜欢的牛肯定是没有出边的

由性质一可知我们可以进行缩点

重建图之后是一个有向无环图
由性质二可知能当明星的牛肯定是有向无环图的终点

终点也可能是缩点而得来的，所以要检查终点所对应的原来的强连通分量

#include<iostream>
#include<queue>
#include<cstring>
#define N 200001
using namespace std;
struct Edge{
	int na,np;
}e[N],dag[N];
int head[N],head2[N],num2,num,now,n,m,fr,to,w[N],vis[N],dfn[N],out,lian[N],chu[N],low[N],times,stnum[N],stk[N],stks,maxn;
queue<int>q;
inline void add(int f,int t){
	e[++num].na=head[f];
	e[num].np=t;
	head[f]=num;
}
inline void add2(int f,int t){
	dag[++num2].na=head2[f];
	dag[num2].np=t;
	head2[f]=num2;
}
inline void tarjan(int n){
	dfn[n]=++times;
	low[n]=times;
	stk[++stks]=n;
	for(int i=head[n];i;i=e[i].na){
		if(!dfn[e[i].np]){
			tarjan(e[i].np);
			low[n]=min(low[n],low[e[i].np]);
		}
		else if(!vis[e[i].np]){
			low[n]=min(low[n],dfn[e[i].np]);
		}
	}
	if(dfn[n]==low[n]){
		vis[n]=n;
		while(stk[stks]!=n){
			stnum[n]+=1;
			vis[stk[stks]]=n;
			stks-=1;
		}
		stnum[n]+=1;
		stks-=1;
	}
}
int main(){
	cin>>n>>m;
	for(int i=1;i<=m;i++){
		cin>>fr>>to;
		add(fr,to);
	}
	for(int i=1;i<=n;i++){
		if(!dfn[i]) tarjan(i);
	}
	for(int i=1;i<=n;i++){
		for(int o=head[i];o;o=e[o].na){
			if(vis[i]==vis[e[o].np]) continue;
			chu[vis[i]]+=1;
		}
	}
	for(int i=1;i<=n;i++){
		if(!chu[i]&&vis[i]==i){
			if(out){
				cout<<"0";return 0;
			}
			out=stnum[vis[i]];
		}
	}
	cout<<out;
}

消息扩散

这道题太水了所以就只写个思路：

统计入度为0的点的个数

结束了

[Wind Festival]Running In The Sky

这道题我给个好评
首先亮度和是很简单的，跑个DAG dp就可以了

重要的是路径上最大的亮度值

不要以为跑dp的时候顺便取个(maxn)最大值就行了，看题

如果有多条符合条件的路径，输出能产生最大单只风筝亮度的答案

也就是说在保证了第一问的前提下才能选最大值

我们很容易想到：在跑dp的时候顺便将每个点的最大值都记录下来
然后呢？

然后我们用一个变量将最大值答案位置记录下来

这个位置不是随便更新的，只有在总和最大值更新的时候才能更新

这里的更新是指：
现在的总和值大于等于原来的总和值

跑完了这些，答案也就呼之欲出了

注意

• 在初始化dp压队列的时候也要统计

#include<iostream>
#include<queue>
#include<cstring>
#define N 1000001
using namespace std;
struct Edge{
	int na,np;
}e[N],dag[N];
int head[N],head2[N],num2,num,now,n,m,fr,to,w[N],vis[N],dfn[N],lian[N],lian2[N],maxst[N],ru[N],low[N],times,stnum[N],stk[N],stks,maxn,wei,maxn2;
queue<int>q;
inline void add(int f,int t){
	e[++num].na=head[f];
	e[num].np=t;
	head[f]=num;
}
inline void add2(int f,int t){
	dag[++num2].na=head2[f];
	dag[num2].np=t;
	head2[f]=num2;
}
inline void tarjan(int n){
	dfn[n]=++times;
	low[n]=times;
	stk[++stks]=n;
	for(int i=head[n];i;i=e[i].na){
		if(!dfn[e[i].np]){
			tarjan(e[i].np);
			low[n]=min(low[n],low[e[i].np]);
		}
		else if(!vis[e[i].np]){
			low[n]=min(low[n],dfn[e[i].np]);
		}
	}
	if(dfn[n]==low[n]){
		vis[n]=n;
		while(stk[stks]!=n){
			stnum[n]+=w[stk[stks]];
			maxst[n]=max(maxst[n],w[stk[stks]]);
			vis[stk[stks]]=n;
			stks-=1;
		}
		stnum[n]+=w[stk[stks]];
		maxst[n]=max(maxst[n],w[stk[stks]]);
		stks-=1;
	}
}
int main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++) cin>>w[i];
	for(int i=1;i<=m;i++){
		cin>>fr>>to;
		add(fr,to);
	}
	for(int i=1;i<=n;i++){
		if(!dfn[i]) tarjan(i);
	}
	for(int i=1;i<=n;i++){
		for(int o=head[i];o;o=e[o].na){
			if(vis[i]!=i&&vis[e[o].np]!=e[o].np) continue;
			if(vis[i]==vis[e[o].np]) continue;
			add2(vis[i],vis[e[o].np]);
			ru[vis[e[o].np]]+=1;
		}
	}
	for(int i=1;i<=n;i++){
		if(!ru[i]){
			q.push(i);
			lian[i]=stnum[i];
			lian2[i]=maxst[i];
			if(maxn<stnum[i]){
				maxn=stnum[i];
				wei=i;
			}
			else if(maxn==stnum[i]){
				wei=(lian2[wei]>=lian2[i]?wei:i);
			}
		}
	}
	while(q.size()){
		now=q.front();
		q.pop();
		for(int i=head2[now];i;i=dag[i].na){
			ru[dag[i].np]-=1;
			lian[dag[i].np]=max(lian[dag[i].np],lian[now]+stnum[dag[i].np]);
			lian2[dag[i].np]=max(lian2[now],maxst[dag[i].np]);
			if(maxn<lian[dag[i].np]){
				maxn=lian[dag[i].np];
				wei=dag[i].np;
			}
			else if(maxn==lian[dag[i].np]){
				wei=(lian2[wei]>=lian2[dag[i].np]?wei:dag[i].np);
			}
			if(!ru[dag[i].np]) q.push(dag[i].np);
		}
	}
	cout<<maxn<<" "<<lian2[wei];
}

技巧

缩点其实没啥技巧，就是我发现(stnum)这个数组原本是记录某个强连通分量集合中强连通分量的点的个数
但是在某些题目中这个数组是没用的
我们可以用这个数组来记录这个强连通分量所有点权（边权）的和