更新记录
【1】2020.06.23-20:13
- 1.完善KMP内容
- 2.一点Trie树内容
- 3.AC自动机(弱化版)思想
【2】2020.06.24-09:19
- 1.完善Trie树内容
【3】2020.06.24-22:47
- 1.完善AC自动机(弱化版)内容
目录
- KMP字符串匹配
- Trie树(字典树)
- AC自动机
正文
KMP前言
ABOUT 暴力
如果你不会:
return 是新手?"别着急慢慢来,这篇博客可能不适合你":"暴力你再不会就趁早退役吧"
ABOUT KMP
KMP它就是普及的坎,过去就过去,过不去等死
其实没那么严重,前缀树也能打
翻找了很多关于KMP的博客,发现能让人真正理解这个算法的少之又少
所以我根据自己的理解来介绍一下这个算法,希望能帮到一些OIer
朴素算法
时间复杂度:(O(nm))
实质就是暴力匹配,这里不过多介绍
KMP
为了方便讲述,我们先明确几个概念
- G位前(后)缀
一个字符串的G位前(后)缀就是它前(后)G个字符组成的字符串
- 例如字符串
abgakdsf的3位前缀是abg,五位后缀是akdsf
- 最大相同前后缀
满足以下两个条件:
- G位前缀与G位后缀相同
- 在满足上一条的情况下使得G最大
- 例如字符串
abcdbabc的最大相同前后缀是abc
先举个例子,我们要在abcaabcdabcaabcaabc中查找abcab
第一次匹配:
abcaabcdabcaabcaabc
||||X
abcab
普通的来看,这个字符不匹配就应该往后移动一位,然后继续进行匹配
但是这样完全将有用的信息忽略了
第一次匹配已经知道了前四个是abca
此时我们直接将字符串移动某个偏移量
abcaabcdabcaabcaabc
|
abcaa
然后继续进行匹配
某个偏移量到底是啥呢?
设主串M,模式T在进行匹配时
(M[i-j];M[i-j+1]cdots M[i])与(T[0]cdots T[j])在进行匹配的时候
前(j-1)位完全匹配,在第(j)位失配
如果
(T[0];T[1]cdots T[j-1]
e T[1];T[2]cdots T[j])
那么
(T[1];T[2]cdots T[j]
e M[i-j];M[i-j+1]cdots M[i])
所以当在某处失配的时候,我们去找这个字符串的最大相同前后缀
记录G的值,然后从G+1位继续匹配
这个G就是上文所说的某个偏移量
这个操作的正确性显然
在KMP算法中,我们定义一个next数组
第i位记录前i-1位最大G值
(当然也有用第i位记录前i位最大G值的,这里笔者习惯用前者)
那么如何去求next数组每一项的值呢?
我们用模式串自己匹配自己即可
即主串为T,模式串也为T
void getnext(){
next[0]=-1;
for(int i=0,j=-1;i<=s.length();){
if(j==-1||s[i]==s[j])
next[++i]=++j;
else
j=next[j];
}
}
下面放一段运行过程
abcaabcdabcaabcaabc
i:0 j:-1
-1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
i:1 j:0
-1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
i:1 j:-1
-1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
i:2 j:0
-1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
i:2 j:-1
-1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
i:3 j:0
-1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
i:4 j:1
-1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
i:4 j:0
-1 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0
i:5 j:1
-1 0 0 0 1 1 2 0 0 0 0 0 0 0 0 0 0 0 0
i:6 j:2
-1 0 0 0 1 1 2 3 0 0 0 0 0 0 0 0 0 0 0
i:7 j:3
-1 0 0 0 1 1 2 3 0 0 0 0 0 0 0 0 0 0 0
i:7 j:0
-1 0 0 0 1 1 2 3 0 0 0 0 0 0 0 0 0 0 0
i:7 j:-1
-1 0 0 0 1 1 2 3 0 0 0 0 0 0 0 0 0 0 0
i:8 j:0
-1 0 0 0 1 1 2 3 0 1 0 0 0 0 0 0 0 0 0
i:9 j:1
-1 0 0 0 1 1 2 3 0 1 2 0 0 0 0 0 0 0 0
i:10 j:2
-1 0 0 0 1 1 2 3 0 1 2 3 0 0 0 0 0 0 0
i:11 j:3
-1 0 0 0 1 1 2 3 0 1 2 3 4 0 0 0 0 0 0
i:12 j:4
-1 0 0 0 1 1 2 3 0 1 2 3 4 5 0 0 0 0 0
i:13 j:5
-1 0 0 0 1 1 2 3 0 1 2 3 4 5 6 0 0 0 0
i:14 j:6
-1 0 0 0 1 1 2 3 0 1 2 3 4 5 6 7 0 0 0
i:15 j:7
-1 0 0 0 1 1 2 3 0 1 2 3 4 5 6 7 0 0 0
i:15 j:3
-1 0 0 0 1 1 2 3 0 1 2 3 4 5 6 7 4 0 0
i:16 j:4
-1 0 0 0 1 1 2 3 0 1 2 3 4 5 6 7 4 5 0
i:17 j:5
-1 0 0 0 1 1 2 3 0 1 2 3 4 5 6 7 4 5 6
i:18 j:6
-1 0 0 0 1 1 2 3 0 1 2 3 4 5 6 7 4 5 6
KMP主过程:
while(l<m.length()){
if(r==-1||m[l]==s[r]) l++,r++;
else r=next[r];
if(r==s.length()){
cout<<l-s.length()+1<<"
";
r=next[r];
}
}
(想必您已经精通字符串了,快去吊打字典树吧)
Trie树前言
就是字典树(前缀树)啊
实现
每个节点有N个儿子,一个颜色标记
N取决于字符的个数,比如我插入的单词中只有小写字母,N开26即可
Trie树节点的定义:
int k=1;
struct Trie{
int trie[N];
int color;
}t[10001];
G位前缀相同的字符串,共用一个长度为G的链,在G+1处产生分支
[ A example ]
那么插入两个单词inne,innd,询问inne是否在字典树中
- 插入时循环每一位,如果节点存在就继续访问,不存在就新建,k值自增
- 询问时循环每一位,如果节点存在就继续访问,不存在就返回0
[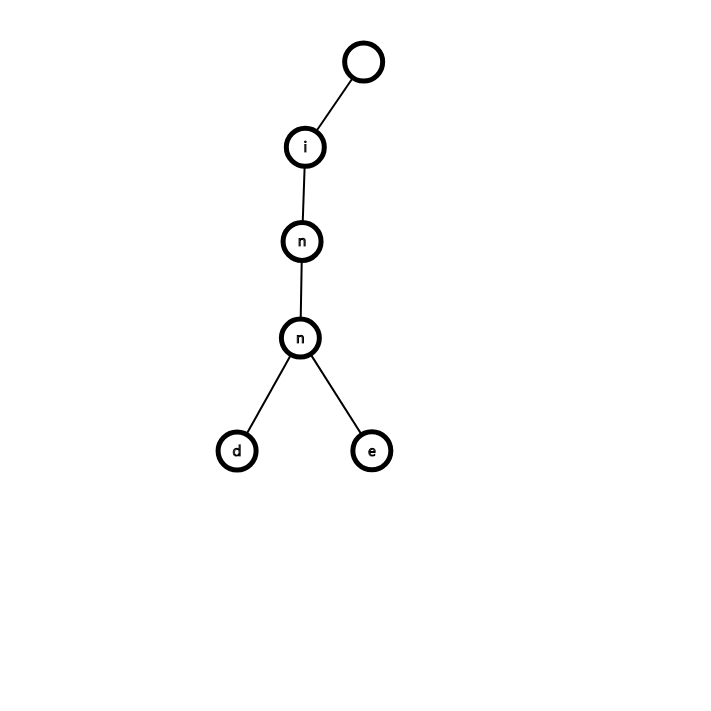 ]
]
然后我们询问单词inn是否在Trie树中
显然inn在树中,但是我们并没有插入这个单词
这时候就要靠颜色标记了
对于一个字符串,在其最后一个字符所在的节点上将颜色标记置为1,代表我插入这个单词了
[.png) ]
]
我们回归刚才的例子,插入单词时e与d的节点的颜色标记标为1,别的不管
那么经过修改后的询问:
- 询问时循环每一位,如果节点存在就继续访问,不存在就返回0,如果字符串最后一个字符所在的节点的颜色标记为1返回1,否则返回0
再次查找inn,虽然能找到,但是我们发现n所对应的节点颜色标记为0
说明没有这个单词
Trie树基本思想结束
插入与查询代码实现:
void insert(string a){
int c,p=0;
for(int i=0;i<a.length();i++){
c=a[i]-'a';
if(!t[p].trie[c])
t[p].trie[c]=k++;
p=t[p].trie[c];
}
t[p].color=1;
}
bool search(string a){
int c,p=0;
for(int i=0;i<a.length();i++){
c=a[i]-'a';
if(!t[p].trie[c])
return 0;
p=t[p].trie[c];
}
return t[p].color==1;
}
AC自动机
没有前言!
在Trie树上查找单词时,用KMP思想进行加速
AC自动机(基本)思想结束
#include<iostream>
#include<queue>
using namespace std;
#define NUM 26
struct Trie{
int trie[NUM];
int e,fail;
}t[1000010];
int tot,n;
string in;
inline void insert(string s){
int c=0,p=0;
for(int i=0;i<s.length();i++){
c=s[i]-'a';
if(!t[p].trie[c])
t[p].trie[c]=++tot;
p=t[p].trie[c];
}
t[p].e+=1;
}
inline void build(){
queue<int>q;int f=0;
for(int i=0;i<NUM;i++)
if(t[0].trie[i])
q.push(t[0].trie[i]);
while(q.size()){
f=q.front();q.pop();
for(int i=0;i<NUM;i++){
if(t[f].trie[i]){
t[t[f].trie[i]].fail=t[t[f].fail].trie[i];
q.push(t[f].trie[i]);
}
else
t[f].trie[i]=t[t[f].fail].trie[i];
}
}
}
inline int query(string s){
int c=0,p=0,sum=0;
for(int i=0;i<s.length();i++){
c=s[i]-'a';
p=t[p].trie[c];
for(int o=p;o&&t[o].e!=-1;o=t[o].fail){
sum+=t[o].e;
t[o].e=-1;
}
}
return sum;
}
int main(){
ios::sync_with_stdio(0);
cin>>n;
for(int i=0;i<n;i++){
cin>>in;
insert(in);
}
build();
cin>>in;
cout<<query(in);
}
(您觉得笔者讲的太简单,自己是字符串专家不需要看,那就快去吊打NOI/CTSC/IOI吧)