Let's call an undirected graph G=(V,E)G=(V,E) relatively prime if and only if for each edge (v,u)∈E(v,u)∈E GCD(v,u)=1GCD(v,u)=1 (the greatest common divisor of vv and uu is 11). If there is no edge between some pair of vertices vv and uu then the value of GCD(v,u)GCD(v,u) doesn't matter. The vertices are numbered from 11 to |V||V|.
Construct a relatively prime graph with nn vertices and mm edges such that it is connected and it contains neither self-loops nor multiple edges.
If there exists no valid graph with the given number of vertices and edges then output "Impossible".
If there are multiple answers then print any of them.
The only line contains two integers nn and mm (1≤n,m≤1051≤n,m≤105) — the number of vertices and the number of edges.
If there exists no valid graph with the given number of vertices and edges then output "Impossible".
Otherwise print the answer in the following format:
The first line should contain the word "Possible".
The ii-th of the next mm lines should contain the ii-th edge (vi,ui)(vi,ui) of the resulting graph (1≤vi,ui≤n,vi≠ui1≤vi,ui≤n,vi≠ui). For each pair (v,u)(v,u)there can be no more pairs (v,u)(v,u) or (u,v)(u,v). The vertices are numbered from 11 to nn.
If there are multiple answers then print any of them.
5 6
Possible
2 5
3 2
5 1
3 4
4 1
5 4
6 12
Impossible
Here is the representation of the graph from the first example: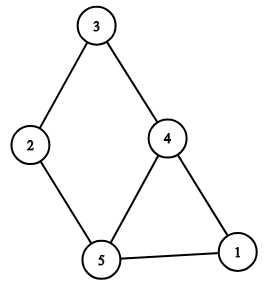
没有想到正解居然是暴力。当时想n^2longn肯定过不了....
但是由于m是1e5,所以循环不到n^2次。
#include <bits/stdc++.h>
#define maxn 100005
using namespace std;
int main()
{
vector<pair<int,int> > v;
int cnt=0;
int n,m;
cin>>n>>m;
if(m<n-1)
{
cout<<"Impossible"<<endl;
return 0;
}
for(int i=1;i<=n;i++)
{
for(int j=i+1;j<=n;j++)
{
if(j!=i&&__gcd(i,j)==1)
{
v.push_back(make_pair(i,j));
cnt++;
if(cnt==m)
{ cout<<"Possible"<<endl;
for(int i=0;i<v.size();i++)
{
cout<<v[i].first<<" "<<v[i].second<<endl;
}
return 0;
}
}
}
}
cout<<"Impossible"<<endl;
return 0;
}