http://acm.hdu.edu.cn/showproblem.php?pid=4303
题意:
给出一棵树,树上的每一个节点都有一个权值,每条边有一个颜色,如果一条路径上相邻边的颜色都是不同的,那么它就是符合要求的。求出所有符合要求的路径上的节点的权值和。
思路:
num[u]表示u节点下有几条符合要求的子树路径,sum[u]表示u为起点(或者终点也可以)往子树方向符合要求的路径权值和。
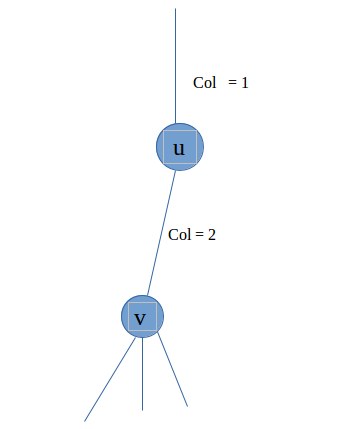
如图,u的父节点颜色为1,u->v的边颜色为2,那么此时u可以和v相连,num[v]就是v保留的路径数,这些保留下来的都是和u->v颜色不同的,那么在原有的sum[v]上,因为有num[v]条路径,那么u节点可以连num[v]次,所以此时sum[u]+=sum[v]+num[v]*val[u], num[u]+=num[v]。
但是这样的话处理了u作为端点的情况,还存在一种情况就是u的两个子节点相连。这里可以用map来记录不同颜色的路径数和不同颜色的权值总和。统一处理即可。
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<map> 5 using namespace std; 6 const int maxn = 300000 + 5; 7 typedef long long ll; 8 9 int n,tot; 10 int head[maxn], val[maxn],num[maxn]; 11 ll sum[maxn]; 12 ll ans; 13 14 struct node 15 { 16 int v,col,next; 17 }e[2*maxn]; 18 19 20 void addEdge(int u,int v,int col) 21 { 22 e[tot].v = v; 23 e[tot].col = col; 24 e[tot].next = head[u]; 25 head[u] = tot++; 26 } 27 28 29 void dfs(int u,int fa,int prec) 30 { 31 num[u] = 1; 32 sum[u] = val[u]; 33 map<int,ll> mpNum, mpSum; 34 ll temp = 0, tempNum = 0, tempSum = 0; 35 for(int i=head[u];i!=-1;i=e[i].next) 36 { 37 int v = e[i].v; 38 int col = e[i].col; 39 if(v == fa) continue; 40 dfs(v,u,col); 41 temp = sum[v] + (ll)num[v]*val[u]; 42 if(col != prec) 43 { 44 num[u] += num[v]; 45 sum[u] += temp; 46 } 47 tempNum += num[v]; 48 tempSum += temp; 49 mpNum[col] += num[v]; 50 mpSum[col] += temp; 51 } 52 ans += tempSum; 53 temp = 0; 54 for(int i=head[u];i!=-1;i=e[i].next) 55 { 56 int v = e[i].v; 57 int col = e[i].col; 58 if(v == fa) continue; 59 temp += sum[v]*(tempNum - mpNum[col]) + num[v]*(tempSum - mpSum[col]); 60 } 61 ans += temp/2; 62 } 63 64 int main() 65 { 66 while(~scanf("%d",&n)) 67 { 68 ans = 0; 69 tot = 0; 70 memset(head,-1,sizeof(head)); 71 for(int i=1;i<=n;i++) scanf("%d",&val[i]); 72 for(int i=1;i<n;i++) 73 { 74 int u,v,w; 75 scanf("%d%d%d",&u,&v,&w); 76 addEdge(u,v,w); 77 addEdge(v,u,w); 78 } 79 dfs(1,0,0); 80 printf("%lld ",ans); 81 } 82 return 0; 83 }