http://acm.split.hdu.edu.cn/showproblem.php?pid=5985
题意:
有多种类型的硬币,每种类型的硬币都有一定的数量,现在每次抛硬币,除去朝下的硬币,知道最后只剩下一个硬币或者没有硬币,最后的硬币便是幸运硬币,求每种类型硬币成为幸运硬币的概率。
思路:
硬币的概率都是单独的,所以我们只需要计算一个硬币的概率情况即可。
设die[i][k]表示第i种硬币在第k次全部被抛弃的概率,易得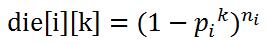 ,用alive[i][k]表示第i种硬币在第k次至少有一个存活的概率就是$1-die[i][k]$。
,用alive[i][k]表示第i种硬币在第k次至少有一个存活的概率就是$1-die[i][k]$。
最后计算就比较简单了, 。
。
这里k取100就已经足够了,因为100次方已经几乎是0了。
1 #include<iostream> 2 #include<algorithm> 3 #include<cstring> 4 #include<cstdio> 5 #include<vector> 6 #include<stack> 7 #include<queue> 8 #include<cmath> 9 #include<map> 10 #include<set> 11 using namespace std; 12 typedef long long ll; 13 typedef pair<int,int> pll; 14 const int INF = 0x3f3f3f3f; 15 const int maxn = 200+5; 16 17 int n,m,num; 18 double p; 19 double die[15][105],alive[15][105]; 20 21 int main() 22 { 23 freopen("in.txt","r",stdin); 24 int T; 25 scanf("%d",&T); 26 while(T--) 27 { 28 scanf("%d",&n); 29 for(int i=1;i<=n;i++) 30 { 31 scanf("%d%lf",&num,&p); 32 for(int k=1;k<=100;k++) 33 { 34 die[i][k]=pow(1.0-pow(p,k*1.0),num*1.0); 35 alive[i][k]=1.0-die[i][k]; 36 } 37 } 38 if(n==1) {puts("1.000000");continue;} 39 40 for(int i=1;i<=n;i++) 41 { 42 double ans=0; 43 for(int k=1;k<=100;k++) 44 { 45 double tmp=1; 46 for(int j=1;j<=n;j++) 47 { 48 if(i!=j) tmp*=die[j][k]; 49 } 50 ans+=(alive[i][k]-alive[i][k+1])*tmp; 51 } 52 printf("%.6f%c",ans,i==n?' ':' '); 53 } 54 } 55 return 0; 56 }