51nod 1040 最大公约数之和（欧拉函数）

http://www.51nod.com/onlineJudge/questionCode.html#!problemId=1040

题意：

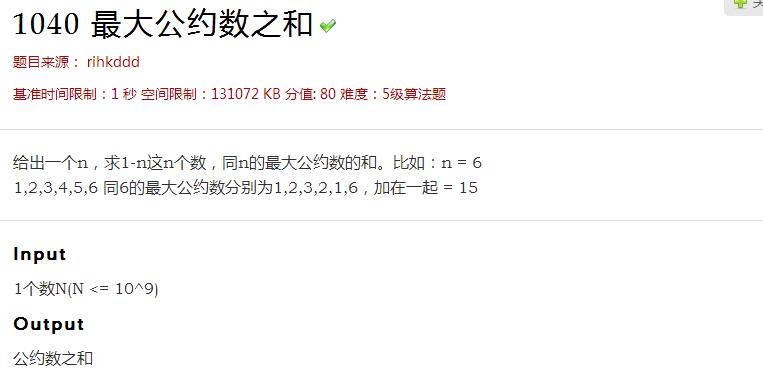
思路：
最大公约数肯定也是在1~n这个范围里的，所以可以枚举所以因子（也就是1~n），计算出每个因子出现的个数，这样就能很快的求得结果。

这里就要用到欧拉函数了，假设现在我们枚举的是i这个因子，那么i出现的次数就是phi（n/i），此时求得数都是与n/i互素的，最后乘以i之后与n的最大公约数就是i。

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<vector>
#include<stack>
#include<queue>
#include<cmath>
#include<map>
#include<set>
using namespace std;
typedef long long ll;
typedef pair<int,int> pll;
const int INF = 0x3f3f3f3f;
const int maxn=1000+5;

int n;

int euler_phi(int n)
{
    int m=sqrt(n+0.5);
    int ans=n;
    for(int i=2;i<=m;i++)  if(n%i==0)
    {
        ans=ans/i*(i-1);
        while(n%i==0)  n/=i;
    }
    if(n>1)  ans=ans/n*(n-1);
    return ans;
}

int main()
{
    //freopen("in.txt","r",stdin);
    while(~scanf("%d",&n))
    {
        ll sum=0;
        for(int i=1;i*i<=n;i++)
        {
            if(n%i==0)
            {
                sum+=euler_phi(n/i)*i;
                if(i!=n/i)
                    sum+=euler_phi(i)*(n/i);
            }
        }
        printf("%lld
",sum);
    }
    return 0;
}