http://acm.hdu.edu.cn/showproblem.php?pid=2242
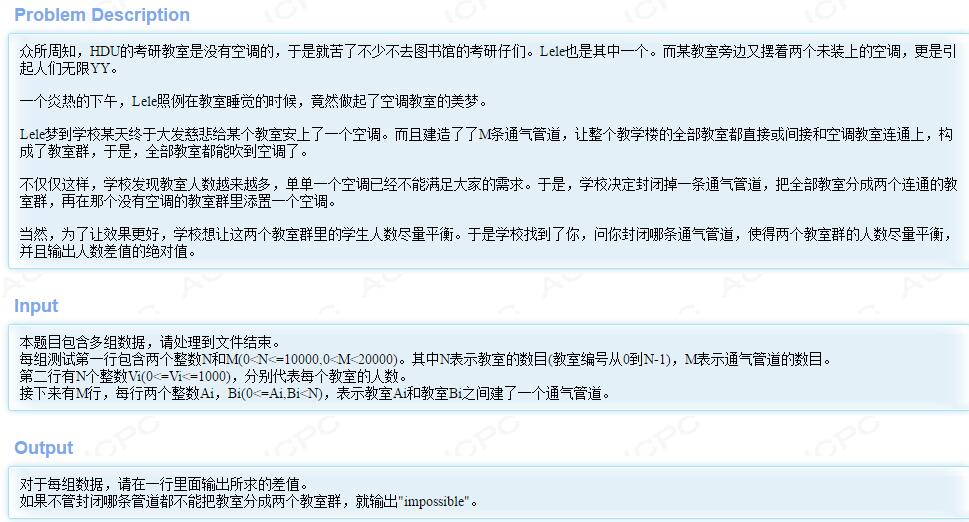
题意:
思路:
首先求一下双连通分量,如果只有一个双连通分量,那么无论断哪根管子,图还是连通的。
最后只需要根据双连通分量重新建图,在树上进行dp,分成两部分的最小差值。这个具体看代码就可以了。
需要注意的是,这道题目是存在重边的,在这个点上我WA了好久,那么怎么处理重边呢?
设置一个重边标记,跳过第一次父亲结点的反向边,但是第二次的话就必须处理,此时就是双连通的了。
简单来说,如果图是没有重边的,那么我们在考虑反向边时,到父亲结点的反向边是不能考虑的,也就是else if(v!=fa) lowu=min(lowu,pre[v])。
但是在这里是存在重边的,所以第一条父亲节点的反向边我们不能去考虑,但是之后就必须要去考虑,因为u,v之间如果有两条及以上的边,那它就是个双连通分量了,如果你用之前的(v!=fa)去判断,那肯定是错误的。
1 #include<iostream> 2 #include<algorithm> 3 #include<cstring> 4 #include<cstdio> 5 #include<sstream> 6 #include<vector> 7 #include<stack> 8 #include<queue> 9 #include<cmath> 10 #include<map> 11 #include<set> 12 using namespace std; 13 typedef long long ll; 14 typedef pair<int,int> pll; 15 const int INF = 0x3f3f3f3f; 16 const int maxn=20000+5; 17 18 int n, m; 19 int tot; 20 int cnt; 21 int scc; 22 int ans; 23 int all_value; 24 int val[maxn]; 25 int head[maxn]; 26 int head2[maxn]; 27 int dfs_clock; 28 int pre[maxn]; 29 int low[maxn]; 30 int eccno[maxn]; 31 int sum[maxn]; 32 33 stack<int> S; 34 35 struct node 36 { 37 int v; 38 int next; 39 }e[80000+5]; 40 41 void addEdge(int u, int v) 42 { 43 e[tot].v=v; 44 e[tot].next=head[u]; 45 head[u]=tot++; 46 } 47 48 void addEdge2(int u, int v) 49 { 50 e[tot].v=v; 51 e[tot].next=head2[u]; 52 head2[u]=tot++; 53 } 54 55 void init() 56 { 57 tot=all_value=scc=dfs_clock=0; 58 memset(head,-1,sizeof(head)); 59 memset(head2,-1,sizeof(head2)); 60 memset(sum,0,sizeof(sum)); 61 memset(pre,0,sizeof(pre)); 62 memset(eccno,0,sizeof(eccno)); 63 } 64 65 int Tarjan(int u, int fa) 66 { 67 int flag=0; //标价重边 68 int lowu=pre[u]=++dfs_clock; 69 S.push(u); 70 for(int i=head[u];i!=-1;i=e[i].next) 71 { 72 int v=e[i].v; 73 if(v==fa && !flag) {flag=1;continue;}//考虑重边的情况,相当重要! 74 if(!pre[v]) 75 { 76 int lowv=Tarjan(v,u); 77 lowu=min(lowu,lowv); 78 } 79 else lowu=min(lowu,pre[v]); 80 } 81 if(pre[u]==lowu) 82 { 83 scc++; 84 for(;;) 85 { 86 int tmp=S.top(); S.pop(); 87 eccno[tmp]=scc; 88 sum[scc]+=val[tmp]; 89 if(tmp==u) break; 90 } 91 } 92 return low[u]=lowu; 93 } 94 95 int dp(int u, int fa) 96 { 97 int ALL=sum[u]; 98 for(int i=head2[u];i!=-1;i=e[i].next) 99 { 100 int v=e[i].v; 101 if(v==fa) continue; 102 ALL+=dp(v,u); 103 104 } 105 ans=min(ans,abs(all_value-2*ALL)); 106 return ALL; 107 } 108 109 int main() 110 { 111 //freopen("in.txt","r",stdin); 112 while(~scanf("%d%d",&n,&m)) 113 { 114 init(); 115 for(int i=0;i<n;i++) {scanf("%d",&val[i]);all_value+=val[i];} 116 while(m--) 117 { 118 int u, v; 119 scanf("%d%d",&u,&v); 120 addEdge(u,v); 121 addEdge(v,u); 122 } 123 for(int i=0;i<n;i++) 124 if(!pre[i]) Tarjan(i,-1); 125 126 if(scc==1) {puts("impossible");continue;} 127 for(int u=0;u<n;u++) 128 { 129 for(int i=head[u];i!=-1;i=e[i].next) 130 { 131 int v=e[i].v; 132 if(eccno[u]!=eccno[v]) addEdge2(eccno[u],eccno[v]); 133 } 134 } 135 ans=INF; 136 dp(1,-1); 137 printf("%d ",ans); 138 } 139 return 0; 140 }