Codeforces 690 C3. Brain Network (hard) LCA

C3. Brain Network (hard)

 

Breaking news from zombie neurology! It turns out that – contrary to previous beliefs – every zombie is born with a single brain, and only later it evolves into a complicated brain structure. In fact, whenever a zombie consumes a brain, a new brain appears in its nervous system and gets immediately connected to one of the already existing brains using a single brain connector. Researchers are now interested in monitoring the brain latency of a zombie. Your task is to write a program which, given a history of evolution of a zombie's nervous system, computes its brain latency at every stage.

Input

The first line of the input contains one number n – the number of brains in the final nervous system (2 ≤ n ≤ 200000). In the second line a history of zombie's nervous system evolution is given. For convenience, we number all the brains by 1, 2, ..., n in the same order as they appear in the nervous system (the zombie is born with a single brain, number 1, and subsequently brains 2, 3, ..., n are added). The second line contains n - 1 space-separated numbers p2, p3, ..., pn, meaning that after a new brain k is added to the system, it gets connected to a parent-brain .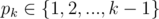

Output

Output n - 1 space-separated numbers – the brain latencies after the brain number k is added, for k = 2, 3, ..., n.

Example

input

6
1
2
2
1
5

output

1 2 2 3 4 

题意：

　　给你一个根节点1，之后每次加一条边，结点的父结点是树中已经得到的结点，问你加完边之后每一次的直径

题解：

　　新直径与加边之前的直径的关系，假设未加边之前是由X,Y这两点组成的链最长，那么答案必然是 max(dis(i,X),dis(i,Y),dis(X,Y));　　

　　这个画图作作假设就看得出

#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
typedef long long LL;
const int N=4e5+110,mods=20090717,inf=2e9+10;

int fa[N][30],dep[N],n,f[N];
vector<int > G[N];
void Lca_dfs(int u,int p,int d) {
    fa[u][0] = p, dep[u] = d;
    for(int i = 0; i < G[u].size(); ++i) {
        int to = G[u][i];
        if(to == p) continue;
        Lca_dfs(to,u,d+1);
    }
}
void Lca_init() {
    Lca_dfs(1,0,0);
    for(int i = 1; i <= 22; ++i) {
        for(int j = 1; j <= n; ++j) {
            if(fa[j][i-1]) {
                fa[j][i] = fa[fa[j][i-1]][i-1];
            } else {
                fa[j][i] = 0;
            }
        }
    }
}
int Lca(int x,int y) {
    if(dep[x] > dep[y]) swap(x,y);
    for(int k = 0; k < 22; ++k) {
        if((dep[y] - dep[x])>>k&1)
            y = fa[y][k];
    }
    if(x == y) return x;
    for(int k = 21; k >= 0; --k) {
        if(fa[x][k] != fa[y][k]) {
            x = fa[x][k];
            y = fa[y][k];
        }
    }
    return fa[x][0];
}
int main() {
    scanf("%d",&n);
    for(int i = 2; i <= n; ++i){
       scanf("%d",&f[i]);
       G[f[i]].push_back(i);
    }
    Lca_init();
    int ans = 0,x = 1,y = 1;
    for(int i = 2; i <= n; ++i) {
        int ux = Lca(i,x);
        int uy = Lca(i,y);
        int nowx,nowy;
        if(x == ux) {
            if(ans < dep[i] - dep[x]) {
                ans = dep[i] - dep[x];
                nowx = i;nowy = x;
            }
        }else {
            if(dep[i] + dep[x] - 2*dep[ux] > ans) {
                ans = dep[i] + dep[x] - 2*dep[ux];
                nowx = i;
                nowy = x;
            }
        }
        if(y == uy) {
            if(ans < dep[i] - dep[y]) {
                ans = dep[i] - dep[y];
                nowx = i;nowy = y;
            }
        }
        else {
             if(dep[i] + dep[y] - 2*dep[uy] > ans) {
                ans = dep[i] + dep[y] - 2*dep[uy];
                nowx = i;
                nowy = y;
            }
        }
        x=  nowx;
        y = nowy;
        cout<<ans<<" ";
    }
    return 0;
}