Codeforces Round #324 (Div. 2)D. Dima and Lisa 数学（素数）

                                                 D. Dima and Lisa

Dima loves representing an odd number as the sum of multiple primes, and Lisa loves it when there are at most three primes. Help them to represent the given number as the sum of at most than three primes.

More formally, you are given an odd numer n. Find a set of numbers pi (1 ≤ i ≤ k), such that

1. 1 ≤ k ≤ 3
2. pi is a prime
3. 

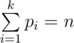
The numbers pi do not necessarily have to be distinct. It is guaranteed that at least one possible solution exists.

Input

The single line contains an odd number n (3 ≤ n < 109).

Output

In the first line print k (1 ≤ k ≤ 3), showing how many numbers are in the representation you found.

In the second line print numbers pi in any order. If there are multiple possible solutions, you can print any of them.

Sample test(s)

input

27

output

3
5 11 11

Note

A prime is an integer strictly larger than one that is divisible only by one and by itself.

题意：给你一个n，让你找出K个（1<=k<=3）素数，它们的和为n

题解：随机素数判断法，

 知道一个大于2的偶数必然存在两个素数和为本身，n-3就可以了

对于n小的数可以打表判断

///1085422276
#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<algorithm>
#include<queue>
#include<cmath>
#include<map>
#include<bitset>
#include<set>
#include<vector>
using namespace std ;
typedef long long ll;
#define mem(a) memset(a,0,sizeof(a))
#define meminf(a) memset(a,127,sizeof(a));
#define TS printf("111111
");
#define FOR(i,a,b) for( int i=a;i<=b;i++)
#define FORJ(i,a,b) for(int i=a;i>=b;i--)
#define READ(a,b,c) scanf("%d%d%d",&a,&b,&c)
#define inf 100000
inline ll read()
{
    ll x=0,f=1;
    char ch=getchar();
    while(ch<'0'||ch>'9')
    {
        if(ch=='-')f=-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9')
    {
        x=x*10+ch-'0';
        ch=getchar();
    }
    return x*f;
}
//****************************************
///****************************************************************
/// Miller_Rabin 算法进行素数测试
///速度快，而且可以判断 <2^63的数
//****************************************************************
const int S=20;///随机算法判定次数，S越大，判错概率越小


///计算 (a*b)%c.   a,b都是long long的数，直接相乘可能溢出的
///  a,b,c <2^63
long long mult_mod(long long a,long long b,long long c)
{
    a%=c;
    b%=c;
    long long ret=0;
    while(b)
    {
        if(b&1){ret+=a;ret%=c;}
        a<<=1;
        if(a>=c)a%=c;
        b>>=1;
    }
    return ret;
}



///计算  x^n %c
long long pow_mod(long long x,long long n,long long mod)//x^n%c
{
    if(n==1)return x%mod;
    x%=mod;
    long long tmp=x;
    long long ret=1;
    while(n)
    {
        if(n&1) ret=mult_mod(ret,tmp,mod);
        tmp=mult_mod(tmp,tmp,mod);
        n>>=1;
    }
    return ret;
}





///以a为基,n-1=x*2^t      a^(n-1)=1(mod n)  验证n是不是合数
///一定是合数返回true,不一定返回false
bool check(long long a,long long n,long long x,long long t)
{
    long long ret=pow_mod(a,x,n);
    long long last=ret;
    for(int i=1;i<=t;i++)
    {
        ret=mult_mod(ret,ret,n);
        if(ret==1&&last!=1&&last!=n-1) return true;//合数
        last=ret;
    }
    if(ret!=1) return true;
    return false;
}

/// Miller_Rabin()算法素数判定
///是素数返回true.(可能是伪素数，但概率极小)
///合数返回false;

bool Miller_Rabin(long long n)
{
    if(n<2)return false;
    if(n==2)return true;
    if((n&1)==0) return false;//偶数
    long long x=n-1;
    long long t=0;
    while((x&1)==0){x>>=1;t++;}
    for(int i=0;i<S;i++)
    {
        long long a=rand()%(n-1)+1;///rand()需要stdlib.h头文件
        if(check(a,n,x,t))
            return false;//合数
    }
    return true;
}

#define maxn 5500
int p[maxn],H[maxn];
vector<int >G;
void init()
{
    mem(H);
    H[1]=1;
    for(int i=2;i<maxn;i++)
    {
        if(!H[i])
        for(int j=i+i;j<maxn;j+=i)
        {
            H[j]=1;
        }
    }
    for(int i=1;i<maxn;i++)
    {
        if(!H[i])
        {
            G.push_back(i);
        }
    }
}
int main()
{
    init();
    int n;
    cin>>n;
    if(n<=5500)
    {
         for(int i=0;i<G.size();i++)if(G[i]==n){
            cout<<1<<endl;
            cout<<G[i]<<endl;return 0;
         }
        for(int i=0;i<G.size();i++)
           for(int j=0;j<G.size();j++)
           if(i!=j&&G[i]+G[j]==n)
        {
            cout<<2<<endl;
            cout<<G[i]<<" "<<G[j]<<endl;
            return 0;
        }
        for(int i=0;i<G.size();i++)
            for(int j=0;j<G.size();j++)
            for(int k=0;k<G.size();k++)
                        if(i!=j&&i!=k&&j!=k&&G[i]+G[j]+G[k]==n)
            {
                cout<<3<<endl;
                cout<<G[i]<<" "<<G[j]<<" "<<G[k]<<endl;return 0;
            }
    }
    else {
       n=n-3;
       for(int i=n-1;i>=1;i--)
       {
           int x=n-i;
           int y=i;
           if(Miller_Rabin(x)&&Miller_Rabin(y))
           {
               cout<<3<<endl;
               cout<<3<<" "<<x<<" "<<y<<endl;return 0;
           }
       }
    }
    return 0;
}