一、列表排序
将无序列表变为有序列表
应用场景: 榜单,表格, 给二分查找用,给其他算法用
二、python实现三种简单排序算法
时间复杂度O(n^2), 空间O(1)
1、冒泡排序
思路:
列表每两个相邻的数,如果前面的比后面的大,那么交换这两个数
代码实现:
# 冒泡排序 @cal_time # 测试执行时间 def bubble_sort(li): for i in range(len(li)-1): # i表示第i趟 # 第i趟无序区位置【0,n-i-1】 for j in range(len(li)-i-1): if li[j] > li[j+1]: li[j], li[j+1] = li[j+1], li[j] # 最好情况 O(n^2) # 平均情况 O(n^2) # 最坏情况 O(n^2) # 优化改进>>> # 思路:如果冒泡排序中执行一趟而没有交换,则列表已经是有序状态,可以直接结束算法。 @cal_time def bubble_sort2(li): for i in range(len(li)): # 表示第i趟 exchange = 0 # 第i趟无序区的位置【0,n-i-1】 n是列表长度 for j in range(len(li)-i-1): if li[j] > li[j+1]: li[j], li[j+1] = li[j+1], li[j] exchange = 1 if not exchange: # 如果遍历一遍没有发生交换,则已经有序,直接返回 return # 最好情况 O(n) # 平均情况 O(n^2) # 最坏情况 O(n^2)
2、选择排序
思路:
一趟遍历记录最小的数,放到第一个位置;
再一趟遍历记录剩余列表中最小的数,继续放置;
...
问题:
怎么选出最小的数
# 找最小值 def find_min(li): min_num = li[0] for i in range(1,len(li)): if li[i] < min_num: min_num = li[i] return min_num # 找最小值的下标 def find_min_pos(li): min_pos = 0 for j in range(1,len(li)): if li[j] < li[min_pos]: min_pos = j return min_pos li = [2,5,8,9,11,15,5,1] print(find_min(li)) # 1 print(find_min_pos(li)) # 7
选择排序:
def select_sort(li): for i in range(len(li)-1): # 第i趟遍历,从0开始 # 第i趟 无序区【i, len(li)-1】 # 找无序区最小数位置,和无序区第一个数交换 min_pos = i for j in range(i+1, len(li)): # 从无序区第二个开始找 if li[j] < li[min_pos]: min_pos = j li[min_pos], li[i] = li[i], li[min_pos] li = list(range(100)) random.shuffle(li) # 打乱列表次序 print(li) select_sort(li) print(li)
比冒泡排序快。
3、插入排序
思路:
列表被分为有序区和无序区两个部分。最初有序区只有一个元素。每次从无序区选择一个元素,插入到有序区的位置,直到无序区变空。
代码:
def insert_sort(li): for i in range(1, len(li)): # i表示第i趟,还表示无序区第一个数的位置 tmp = li[i] j = i - 1 # j 从后往前遍历有序区的指针 while j >= 0 and li[j] > tmp: # j遍历结束或无序区第一位大于j指向的数时跳出循环 li[j + 1] = li[j] # 有序区的第j位往后挪一位 j -= 1 # j 向前指一位 li[j + 1] = tmp # 将tmp插入到有序区j后面一位
三、python实现三种较复杂排序算法
1、快速排序
时间复杂度: O(nlogn)
思路:
取一个元素p(第一个元素),使元素p归位;
列表被p分成两部分,左边都比p小,右边都比p大;
左右两边递归完成排序。
方法一(经典方法):
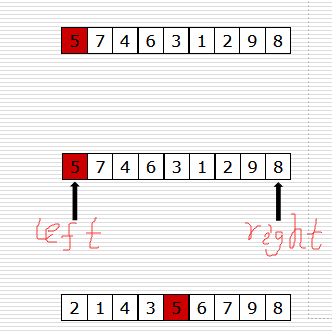
归位思路:
将要归位的数p存起来,此时左游标left指向空
将游标指向的数与p比较,大于放右边,小于放左边(详细操作:
先将右游标right指向的数与p比较,大于p,位置不变,右游标往左移一位,继续比较;小于p,放到left指向的空位置,此时right指向空,然后移left
再将left游标往右移一位指向的数与p比较,小于p,位置不变,left往右移一位,继续比较;大于p,放到right指向的空位置,此时left指向空,然后移right)
当左游标等于右游标时,游标指向的位置就是p要归的位置
注意处理最坏情况(列表倒序)导致递归达到最大深度,从列表中随机取一个与第一个交换位置
代码:
def quick_sort(li, left, right): if left < right: # 递归区域至少有两个元素 mid = partition(li, left, right) # 归位 quick_sort(li, left, mid-1) # 左边 quick_sort(li, mid+1, right) # 右边 def partition(li, left, right): i = random.randint(left, right) # 防止最坏情况(列表有序或倒序)导致递归达到最大深度,从列表中随机取一个与第一个交换位置 li[i], li[left] = li[left], li[i] tmp = li[left] # 将要归位的数存起来 while left < right: while left < right and li[right] >= tmp: right -= 1 # 右边的数大于等于tmp就不动,right游标往左走 li[left] = li[right] # 右边的数小于tmp就往左放 while left < right and li[left] <= tmp: left += 1 # 左边的数小于等于tmp就不动,left游标往右走 li[right] = li[left] # 左边的数大于tmp就往右放 li[left] = tmp # left=right 将tmp归位 return left
方法二(算法导论中的归位方法):
归位思路:
取最后一个元素r归位,
分两个区域,将小于r的数都放到区域一, 剩下的就是大于r的区域二
然后将r与区域二的第一个数交换,就归位成功了
与方法1一样也有python递归最大深度的问题

代码实现:
def partition2(li, left, right): # 区域1:[left, i] 区域2:[i+1, j-1] i = left - 1 # 初始区域1和区域2都空,i指向区域1最后一个数 for j in range(left, right): if li[j] < li[right]: # 放到区域1,i往后移一位 i += 1 li[i], li[j] = li[j], li[i] # 与区域2的第一个数(i+1)交换归为区域1, li[right], li[i+1] = li[i+1], li[right] # 归位 return i+1 # 返回mid
方法三(占用空间的方法):
思路:
每次都取中间的数为归位,尽可能的避免最坏情况导致python递归达最大深度的问题
开三个列表,一个放大于归位数的,一个放小于归位数的,一个放等于归位数的
然后将三个列表拼起来
递归结束条件,列表长度小于等于1,
代码:
def quick_sort3(li): if len(li) <= 1: return li m = li[len(li)//2] # 防止列表本来就是有序或倒序的,导致递归达到最大深度,不取li[0] left = [item for item in li if item < m] right = [item for item in li if item > m] x = [i for i in li if i == m] return quick_sort3(left) + x + quick_sort3(right)
一行实现快速排序:
quick_sort4 = lambda li: li if len(li) <= 1 else quick_sort4([item for item in li[1:] if item <= li[0]]) + [li[0]] + quick_sort4([item for item in li[1:] if item > li[0]])
2、堆排序
堆的概念:
堆是完全二叉树,完全二叉树可以用列表来存储,通过规律可以从父亲找到孩子或从孩子找到父亲,堆中某个节点的值总是不大于或不小于其父节点的值
大根堆:一棵完全二叉树,满足任一节点都比其孩子节点大
小根堆:一棵完全二叉树,满足任一节点都比其孩子节点小
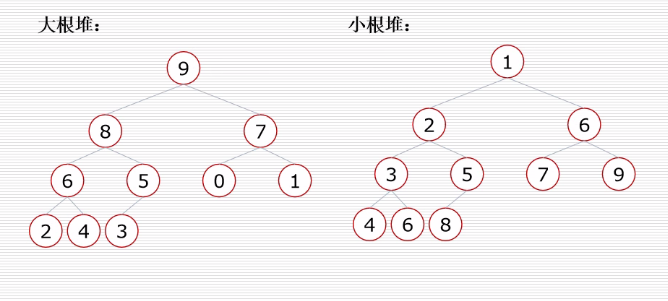
堆排序利用了堆向下调整的特征:节点的左右子树都是堆,但自身不是堆。
向下调整,挨个出数;
通过父节点找子节点:父节点下标为i
则:孩子节点为,2i+1 和 2i+2
通过孩子节点找父节点:孩子节点为j
子节点为左节点,父节点为:(j-1) / 2
子节点为右节点,父节点为:(j-2) / 2
不知道为左子节点还是右子节点: (j-1) // 2
代码:
def sift(li, low, high): ''' 向下调整 :param li: :param low: 堆顶下标 :param high: 堆中最后一个元素下标 :return: ''' tmp = li[low] i = low j = 2 * i + 1 # i, j 两个游标,初始i指向堆顶,j指向堆顶的左孩子 while j <= high: # 第二个结束循环的条件,没有孩子和tmp竞争i这个位置 if j+1 <= high and li[j+1] > li[j]: # 如果右孩子存在并且比左孩子大 j指向右孩子 j += 1 if li[j] > tmp: li[i] = li[j] # 大的数往上调整 i = j # i指向下一个要调整的堆的堆顶 j = 2 * i + 1 # j指向调整堆的堆顶的左孩子 else: break # 第一种循环退出情况,tmp比目前两个孩子都大 li[i] = tmp # i就是tmp要调整到的位置 def heap_sort(li): ''' 堆排序 :param li: :return: ''' # 1. 从列表构造堆,low的值和high的值 n = len(li) # 子节点找父节点: low = (i-1)//2 --> (n-2)//2 --> n//2-1 for low in range(n//2-1, -1, -1): sift(li, low, n-1) # 2. 挨个出数 利用原来的空间存储下来的值,但是这些值不属于堆 for high in range(n-1, -1, -1): # 或range(n-1, 0, -1) li[high], li[0] = li[0], li[high] # 1.把最大的调下来 2.high对应的数调上去 sift(li, 0, high - 1) # 3.调整,high 往前移一个,low为0
3、归并排序
思路:
假设现在的列表分两段有序,如何将其合成一个有序列表, 这个操作称为一次归并。
有了归并之后怎么用?
分解 :将列表越分越小,直至分成一个元素
终止条件:一个元素是有序的。
合并:将两个有序列表归并,列表越来越大。
一次归并:
def merge(li, low, mid, high): ''' 归并 :param li: :param low: :param mid: :param high: :return: ''' i = low j = mid + 1 li_tmp = [] while i <= mid and j <= high: # 两边都有数 if li[i] <= li[j]: li_tmp.append(li[i]) i += 1 else: li_tmp.append(li[j]) j += 1 # i<=mid 和 j<=high 两个条件 只能有一个满足 while i <= mid: li_tmp.append(li[i]) i += 1 while j <= high: li_tmp.append(li[j]) j += 1 # li_tmp 0~high-low 复制回li low~high for i in range(len(li_tmp)): li[low + i] = li_tmp[i]
分解合并:
def merge_sort(li, low, high): if low < high: # 至少两个元素 # print(li[low:high+1], '->', end=' ') mid = (low + high) // 2 # 分解 # print(li[low:mid+1], li[mid+1: high+1]) merge_sort(li, low, mid) # 递归排序左边 merge_sort(li, mid + 1, high) # 递归排序右边 # print(li[low:mid+1], li[mid+1: high+1], '->', end=' ') merge(li, low, mid, high) # 一次归并 合并 # print(li[low:high+1])
小结:
