数据违背基本假设的处理
常见的问题:异方差,自相关,异常值。
异方差
指随机误差项的方差不是一个常数,而是随着自变量的取值变化而变化。
带来的问题:①使用最小二乘法(OLE)求解参数时,参数的估计值虽然无偏,但不是最小方差线性无偏估计。②参数的显著性检验无效。③回归方程的应用效果不理想。
产生原因:①模型缺少某些解释变量,缺省变量本身的方差被包含在随机误差的方差中。②模型本身选取有问题,非线性的选择了线性模型。
其它原因:样本量过少、测量误差、异常数据、时序分析或使用面板数据。
检验:
残差图分析,散点如果随机分布无规律,表明方差符合要求,若有明显的规律性,表明有异方差性。
等级相关系数法,又称斯皮尔曼检验(spearman)
还有其它检验方法:相关图分析、Park检验和Gleiser检验、Goldfeld-Quandt检验、Breusch-Pagan检验、White检验。
用上次的多元线性回归来实操一下。画残差图和密度分布图。
resid = model.resid
plt.scatter(data["mpg"], resid)
plt.savefig("residual.png")
plt.close()
resid.plot.density()
plt.savefig("resid_density.png")
plt.close()
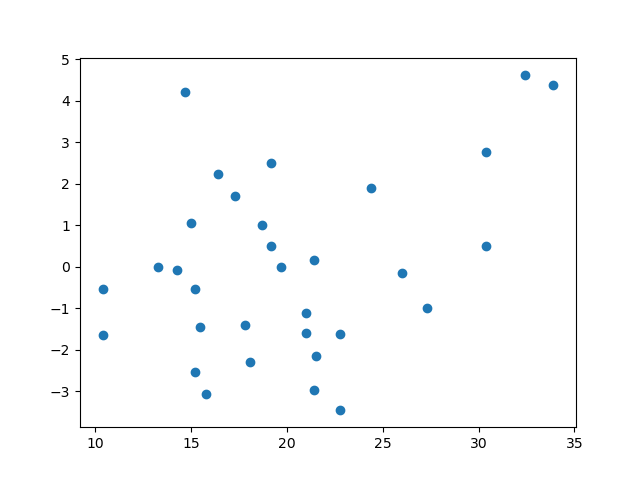
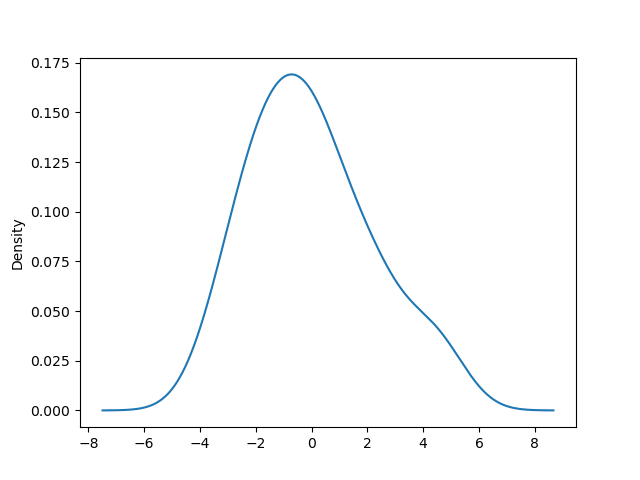
看着还好。
用scipy.stats里的工具来检测异方差性。
print(stats.stats.spearmanr(resid.values, data["mpg"].values))
结果为:
SpearmanrResult(correlation=0.18725359199432956, pvalue=0.30478050953662256)
p > 0.05,没有证据显示有异方差性。
解决异方差的方法,用加权最小二乘法等方法。
自相关
指模型中随机误差项的相关系数不等于0。即变量前后数值之间存在相关关系。
带来的问题:①用最小二乘法求解是虽然无偏,但估计量的方差不是最小。②估计量的方差是有偏的。③显著性检验失效。④存在序列相关时,最小二乘法对抽样误差很敏感。⑤应用效果不理想。
常见原因:①模型遗漏关键变量。②错误的回归函数形式。③蛛网现象。指一个变量对另一个变量的影响有延迟性。④对数据加工整理使数据项之间出现自相关。
检验方法:画et,et+1图,计算自相关系数,DW检验法。
用自相关系数做检验
acf = smt.stattools.acf(resid.values, nlags = 5)
print(acf)
fig = smt.graphics.plot_acf(resid, lags=5, alpha=0.5)
fig.savefig("acf.png")
结果
[ 1. 0.03101277 -0.03869666 0.07033212 -0.23045137 0.02303189]
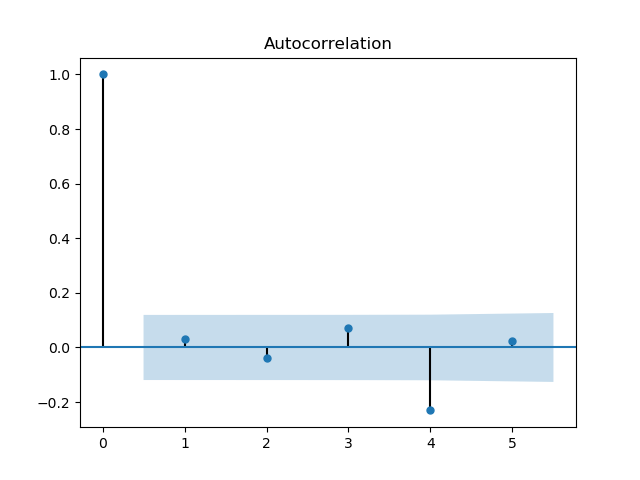
除了两个点,均无自相关性。
消除自相关的方法:迭代法、差分法、BOX-COX变换法等。
DW检验法
dw = durbin_watson(resid)
print(dw)
结果:1.8608933684548286
在0-2区间内,无关联性。
异常值
异常或极端值引起较大残差,影响回归拟合的效果。
成因:数据录入错误,测量错误,数据随机误差,缺少重要自变量,缺少观察数据,存在异方差,模型错误。
一般认为超过±3方差即为异常值。
本文代码: https://github.com/zwdnet/MyQuant/tree/master/17
我发文章的四个地方,欢迎大家在朋友圈等地方分享,欢迎点“在看”。
我的个人博客地址:https://zwdnet.github.io
我的知乎文章地址: https://www.zhihu.com/people/zhao-you-min/posts
我的博客园博客地址: https://www.cnblogs.com/zwdnet/
我的微信个人订阅号:赵瑜敏的口腔医学学习园地