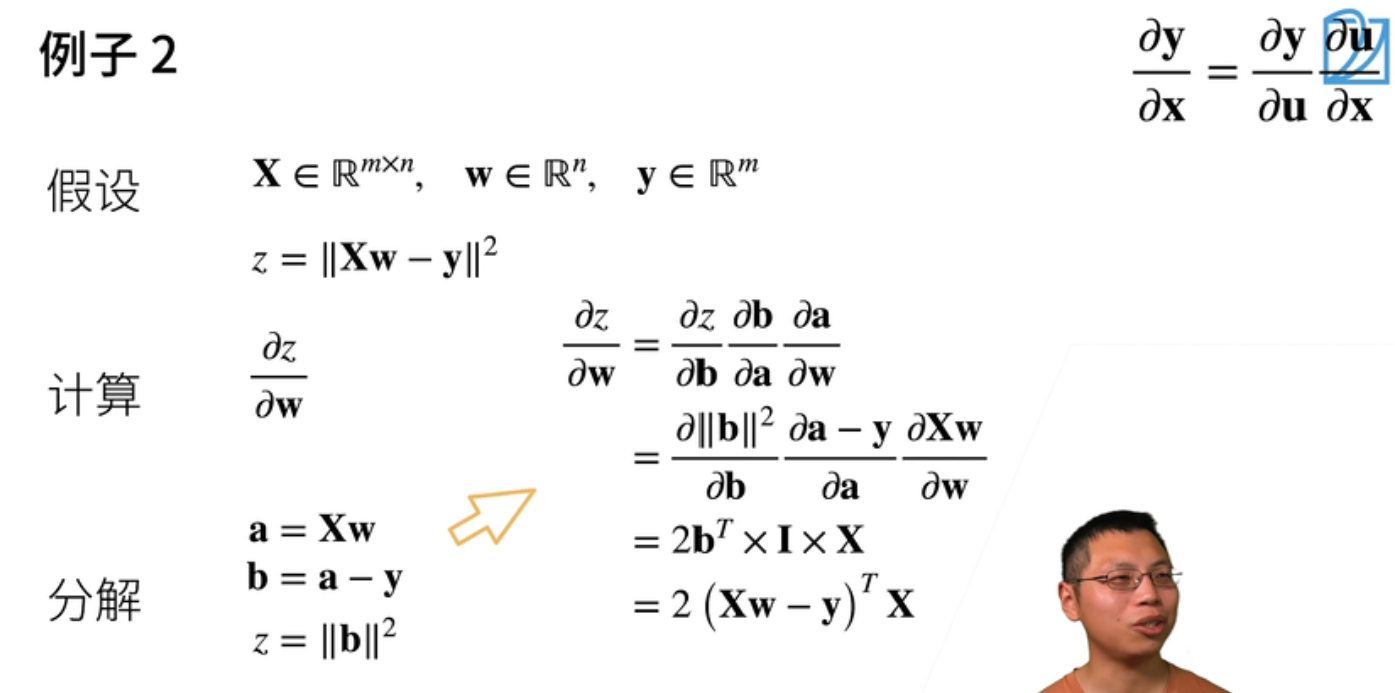向量求导
感谢
[矩阵求导的本质与分子布局、分母布局的本质(矩阵求导——本质篇) - 知乎 (zhihu.com)](https://zhuanlan.zhihu.com/p/263777564#:~:text= 分子布局,就是分子是列向量形式,分母是行向量形式,如 式。 如果这里的 是 实向量函数 的话,结果就是,的矩阵了: 分母布局 ,就是分母是 列向量 形式,分子是 行向量 形式,如 式。)
07 自动求导【动手学深度学习v2】_哔哩哔哩_bilibili
梯度,指向值变化最大的方向,这里都是分子布局
一 函数计算、求导与向量矩阵
考虑一个函数
\[\text{function(input)}
\]
针对\(\text{function}\)、\(\text{input}\)的类型,我们可以将这个函数分类。
1 \(\text{function}\)是一个标量
我们称\(\text{function}\)是一个实值标量函数。用细体小写字母\(f\)表示
1.1 \(\text{input}\)是一个标量
我们称\(\text{function}\)的变元是标量,用细体小写字母\(x\)表示。
计算:输入是标量(\((1,)\)),函数是一个实值标量函数,结果是一个值(标量)(\((1,)\))
求导: 分母(函数值)是标量(\((1,)\)),分子是标量(\((1,)\)),结果是标量(\((1,)\))
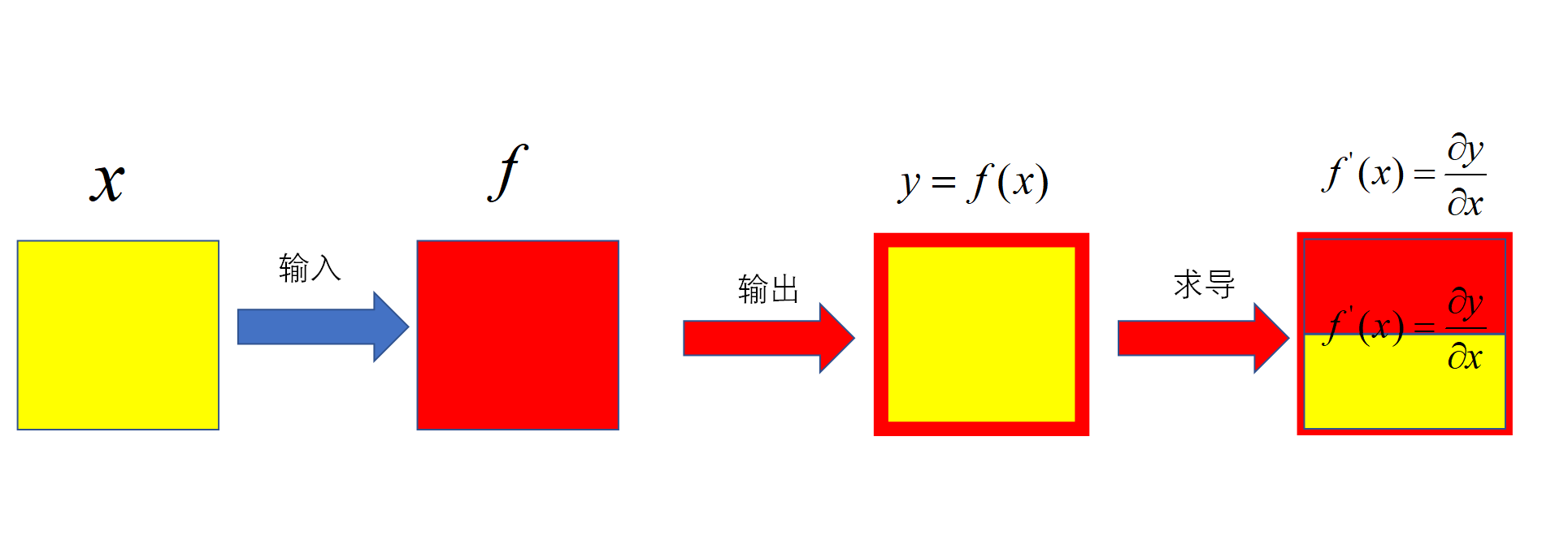
例1
\[f(x) = 2x+2 \\
f'(x)=2
\]
1.2 \(\text{input}\)是一个向量
我们称\(\text{function}\)的变元是向量,用粗体小写字母\(\mathbfcal{x}\)表示。
计算:输入是列向量(\((n,1)n\times 1\)),函数是一个实值标量函数,结果是一个标量(数)(\((1,)\))
求导:分母(函数值)是标量(\((1,)\)),分子是列向量(\((n,1)n\times 1\)),结果是行向量(\((1,n)1\times n\))
\[\mathbfcal{x}= \left[
\begin {array}{1}
x_1 \\
x_2 \\
\vdots \\
x_n
\end{array}
\right ]_{(n,1)}
\\
y=f(\mathbfcal{x})_{(1,)}
\\
f'(\mathbfcal{x})=
\frac{\partial y}{ \partial \mathbfcal{x}} =
\left[
\frac{\partial y}{\partial x_1} ,
\frac{\partial y}{\partial x_2},
\cdots ,
\frac{\partial y}{\partial x_n}
\right ]_{(1,n)}
\]
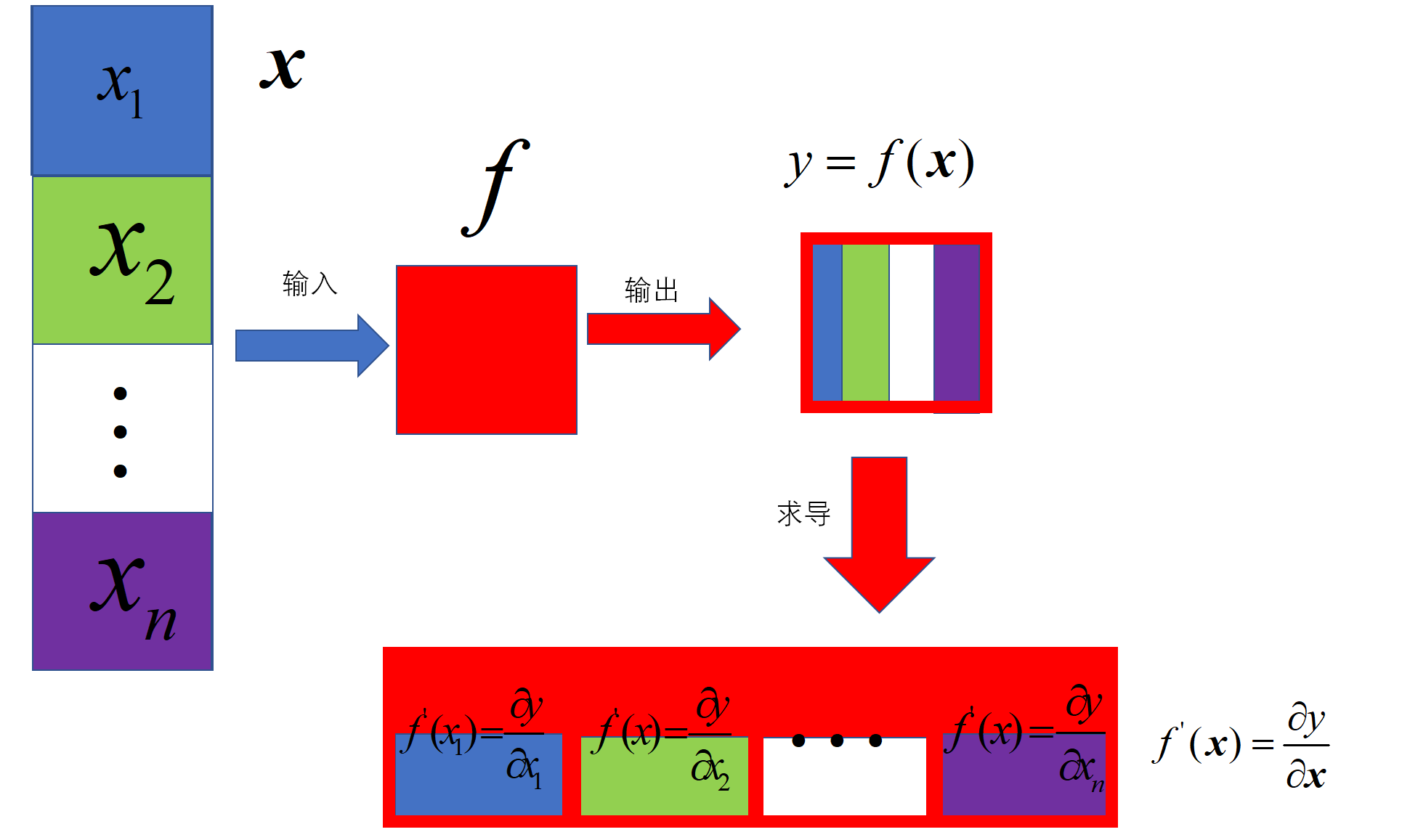
例2
\[\mathbfcal{x}=
\left[
\begin {array}{1}
x_1 \\
x_2
\end{array}
\right ]
\\
y=f(\mathbfcal{x}) = a_1x_1^2+a_2x_2^2+a_3x_1x_2+a_4x_1+a_5x_2+a_6
\\
f'(\mathbfcal{x})=
\frac{\partial y}{ \partial \mathbfcal{x}} =
\left[
\frac{\partial y}{\partial x_1} ,
\frac{\partial y}{\partial x_2}
\right ] = \left[ 2a_1+a_3x_2+a_4, 2a_2+a_3x_1+a_5\right ]
\]
1.3 \(\text{input}\)是一个矩阵
我们称\(\text{function}\)的变元是矩阵,用粗体大写字母\(\symbf{X}\)表示。
计算:输入是矩阵(\((n,k)n\times k\)),函数是一个实值标量函数,结果是一个标量(数)(\((1,)\))
求导:分母(函数值)是标量(\((1,)\)),分子是矩阵(\((n,k)n\times k\)),结果是矩阵(\((k,n)k\times n\))
\[\symbf{X} =
\left (
\begin{matrix}
x_{11} & x_{12} & \cdots & x_{1k} \\
x_{21} & x_{22} & \cdots & x_{2k} \\
\vdots & \vdots & & \vdots \\
x_{n1} & x_{n2} & \cdots & x_{nk} \\
\end{matrix}
\right
)_{(n,k)n\times k} \\
y=f(\symbf{X})_{(1,)} \\
f'(\symbf{X}) =\frac{\partial y}{\partial \symbf{X}} =
\left (
\begin{matrix}
\frac{\partial y}{\partial x_{11}} & \frac{\partial y}{\partial x_{21}} & \cdots & \frac{\partial y}{\partial x_{n1}} \\
\frac{\partial y}{\partial x_{12}} & \frac{\partial y}{\partial x_{22}} & \cdots & \frac{\partial y}{\partial x_{n2}} \\
\vdots & \vdots & & \vdots \\
\frac{\partial y}{\partial x_{1k}} & \frac{\partial y}{\partial x_{2k}} & \cdots & \frac{\partial y}{\partial x_{nk}} \\
\end{matrix}
\right
)_{(k,n)k\times n}
\]
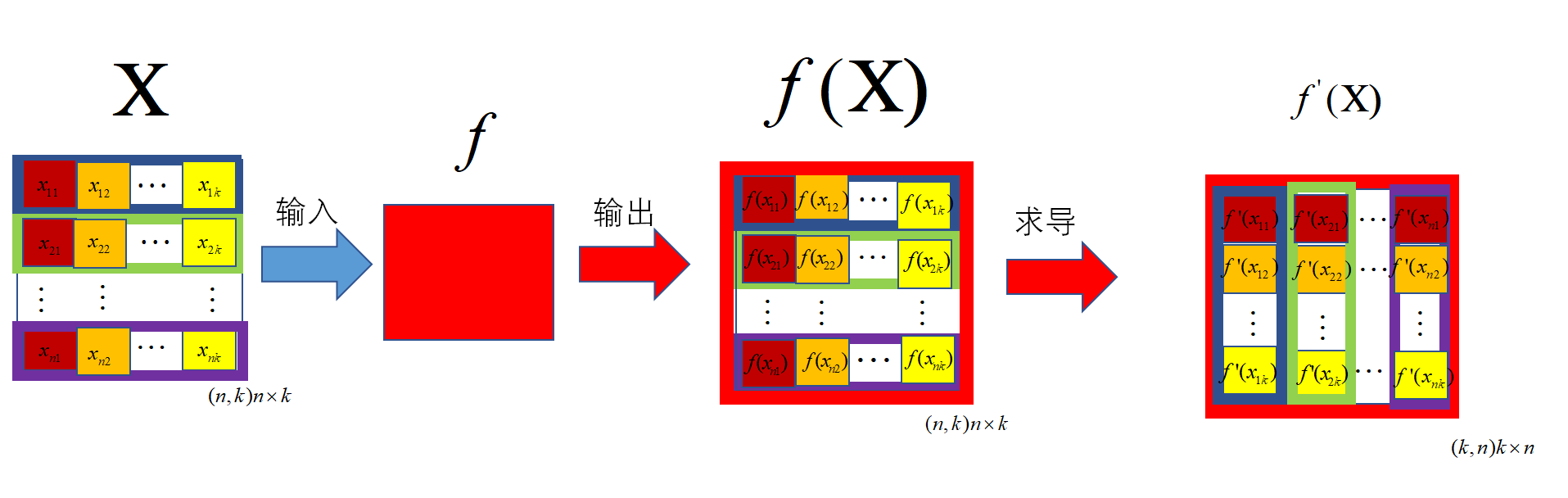
例3
\[\symbf{X} =
\left (
\begin{matrix}
x_{11} & x_{12} \\
x_{21} & x_{22} \\
x_{31} & x_{32} \\
\end{matrix}
\right
)_{(3,2) 3\times 2} \\
y=f(\symbf{X})_{(1,)}=a_1x_{11}^2+a_2x_{12}^2+a_3x_{21}^2+a_4x_{22}^2+a_5x_{31}^2+a_6x_{32}^2 \\
f'(\symbf{X}) =\frac{\partial y}{\partial \symbf{X}} =
\left (
\begin{matrix}
\frac{\partial y}{\partial x_{11}} & \frac{\partial y}{\partial x_{21}} & \frac{\partial y}{\partial x_{31}} \\
\frac{\partial y}{\partial x_{12}} & \frac{\partial y}{\partial x_{22}} & \frac{\partial y}{\partial x_{32}} \\
\end{matrix}
\right) _{(2,3),2\times 3}
=
\left (
\begin{matrix}
2a_1x_{11} & 2a_3x_{21} & 2a_5x_{31} \\
2a_2x_{12} & 2a_4x_{22} & 2a_6x_{32} \\
\end{matrix}
\right) _{(2,3),2\times 3}
\]
2 \(\text{function}\)是一个向量
我们称\(\text{function}\)是一个实向量函数。用粗体小写字母\(\mathbfcal{f}\)表示。
含义: \(\mathbfcal{f}\)是由 若干个\(f\)组成的一个向量

2.1 \(\text{input}\)是一个标量
计算:输入(变元)是标量(\((1,)\)),函数是列向量函数(\((m,1)m \times 1\)),输出结果是列向量(\((m,1)m \times 1\))
求导: 求导分母(函数值)是列向量(\((m,1)m \times 1\)),分子是标量(\((1,)\)),求导结果是列向量(\((m,1)m \times 1\))
\[x \\
\mathbfcal{y} = \mathbfcal{f}(x)=
\left[
\begin {array}{1}
y_1 \\
y_2 \\
\vdots \\
y_n
\end{array}
\right ] \\
\frac{\partial \mathbfcal{y}}{ \partial x} =
\left[
\begin {array}{1}
\frac{\partial y_1}{\partial x} \\
\frac{\partial y_2}{\partial x}\\
\vdots \\
\frac{\partial y_n}{\partial x}
\end{array}
\right ]
\]
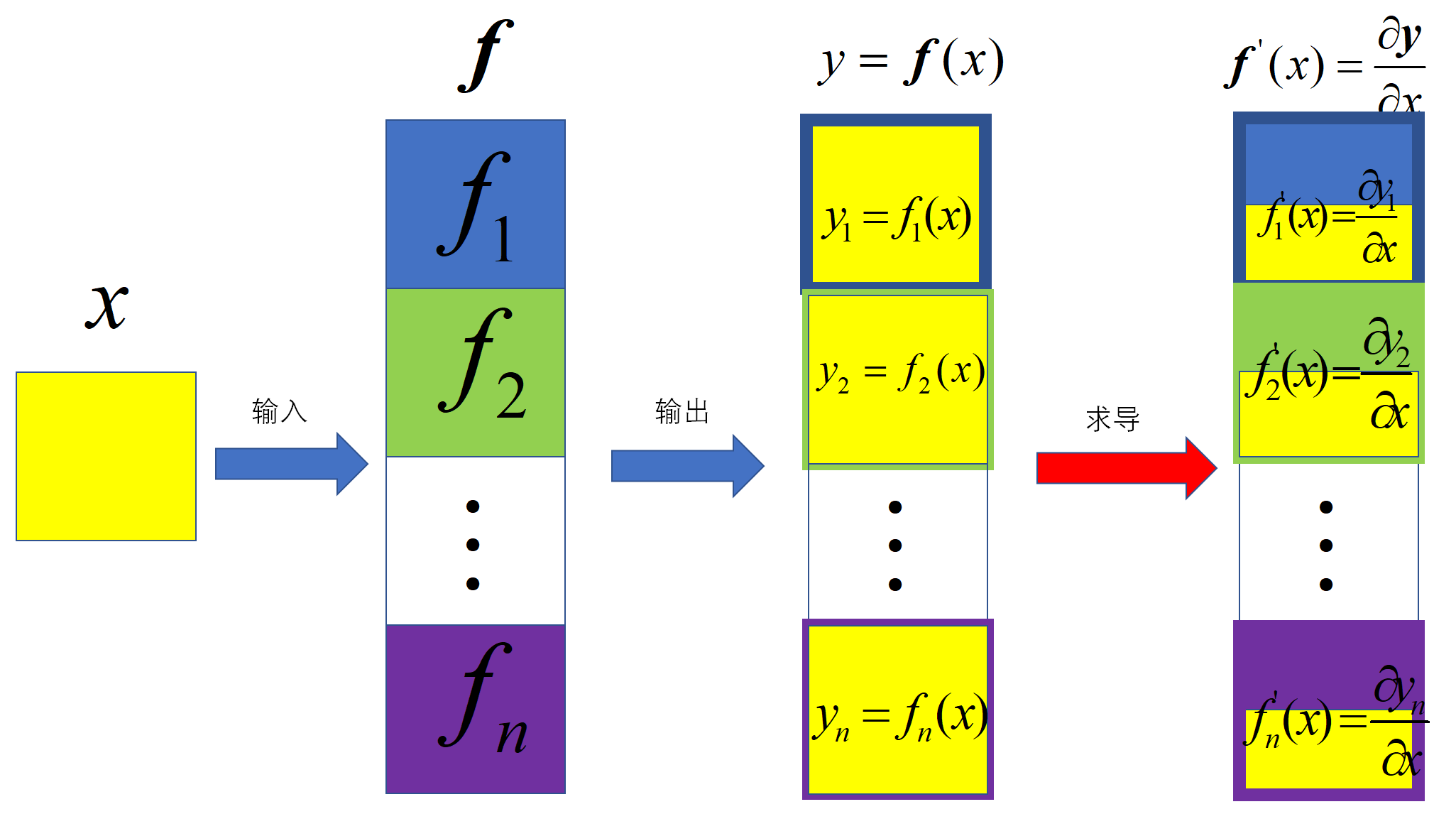
例四
\[x \\
\mathbfcal{y}=\mathbfcal{f}(x)=
\left[
\begin {array}{1}
x+1 \\
2x^2+1 \\
3x^3+1
\end{array}
\right ]_{(3,1)3 \times 1} \\
\mathbfcal{f}'(x)=\frac{\partial \mathbfcal{y}}{ \partial x} =
\left[
\begin {array}{1}
1 \\
4x \\
9x^2
\end{array}
\right ]_{(3,1)3\times 1}
\]
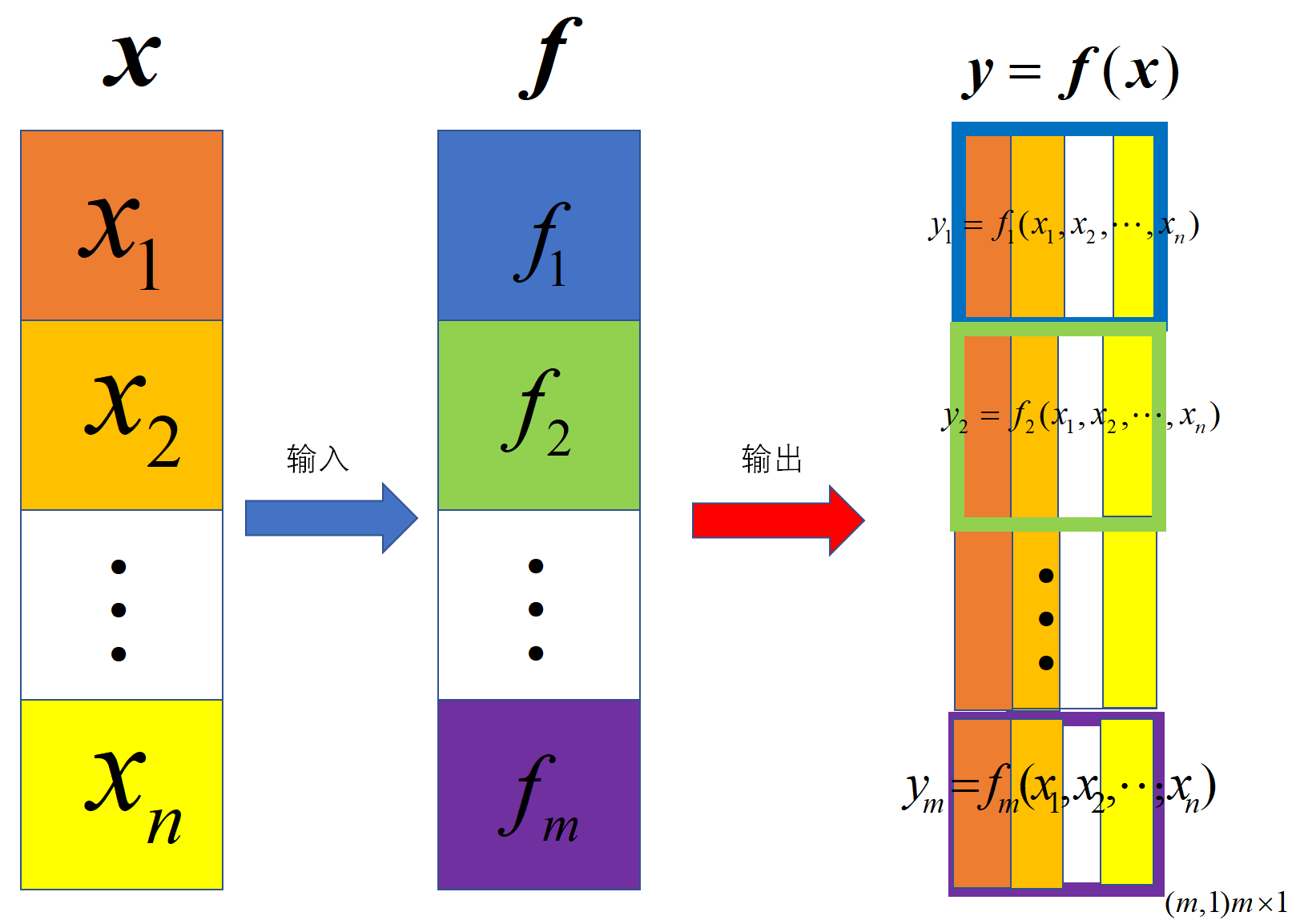
2.2 \(\text{input}\)是一个向量
计算:输入(变元)是向量(\((n,1)n\times 1\)),函数是列向量函数(\((m,1)m \times 1\)),输出结果是列向量(\((m,1)m \times 1\))
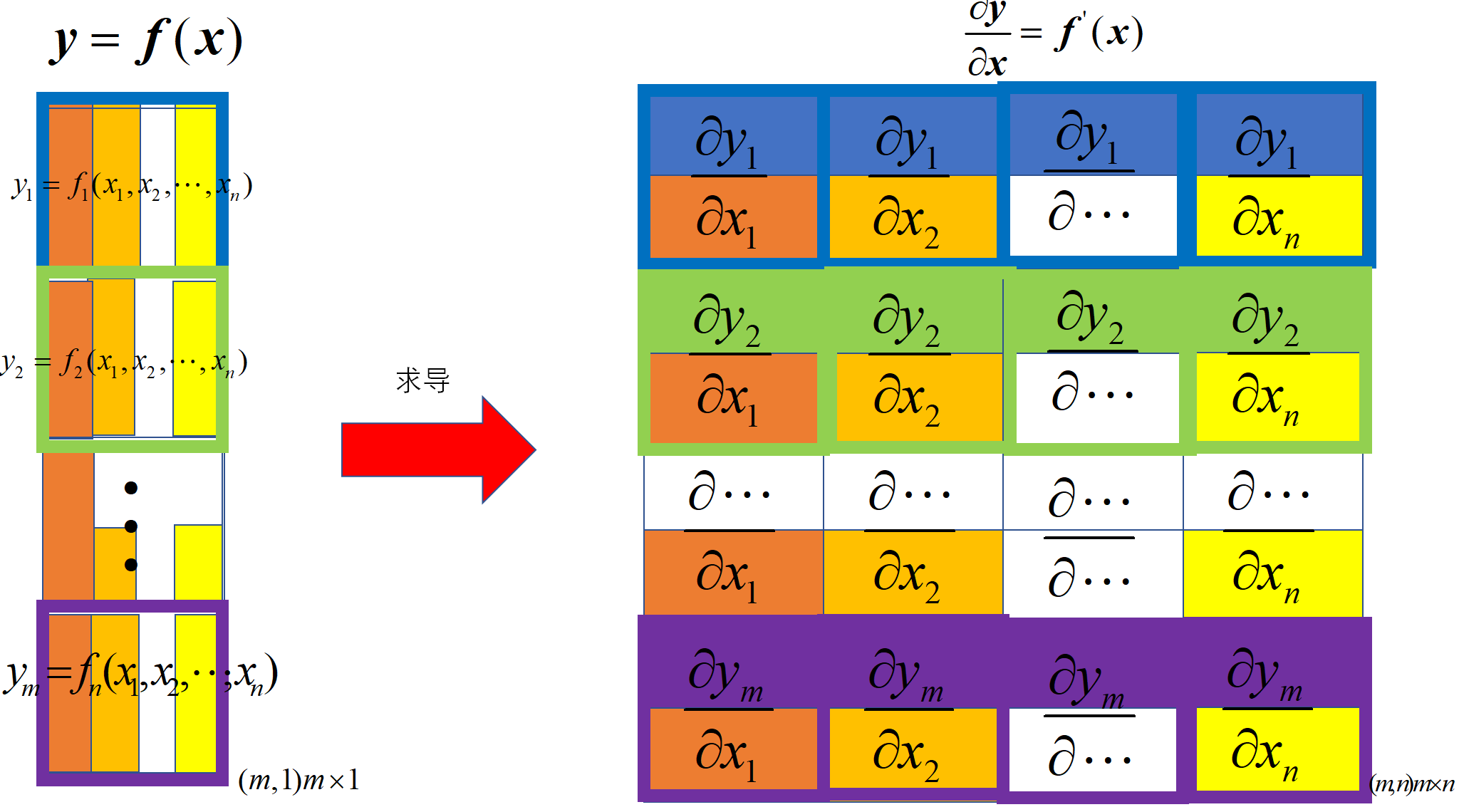
求导: 求导分母(函数值)是列向量(\((m,1)m \times 1\)),分子是向量(\((n,1) n \times 1\)),求导结果是列向量(\((m,n)m \times n\))
Jacobian矩阵
- Jacobian矩阵可被视为是一种组织梯度向量的方法。
- 梯度向量可以被视为是一种组织偏导数的方法。
- 故,Jacobian矩阵可以被视为一个组织偏导数的矩阵。
\[\mathbfcal{x}= \left[
\begin {array}{1}
x_1 \\
x_2 \\
\vdots \\
x_n
\end{array}
\right ]_{(n,1)n\times 1}
\\
\mathbfcal{y} = \mathbfcal{f}(\mathbfcal{x})=
\left[
\begin {array}{1}
y_1 \\
y_2 \\
\vdots \\
y_m
\end{array}
\right ]
=
\left[
\begin {array}{1}
f_1(x_1,x_2,\cdots,x_n) \\
f_2(x_1,x_2,\cdots,x_n) \\
\vdots \\
f_m(x_1,x_2,\cdots,x_n)
\end{array}
\right ]_{(m,1)m\times 1}
\\
\frac{\partial \mathbfcal{y}}{ \partial \mathbfcal{x}} =
\left (
\begin{matrix}
\frac{\partial y_1}{\partial x_{1}} & \frac{\partial y_1}{\partial x_{2}} & \cdots & \frac{\partial y_1}{\partial x_{n}} \\
\frac{\partial y_2}{\partial x_{1}} & \frac{\partial y_2}{\partial x_{2}} & \cdots & \frac{\partial y_2}{\partial x_{n}} \\
\vdots & \vdots & & \vdots \\
\frac{\partial y_m}{\partial x_{1}} & \frac{\partial y_m}{\partial x_{2}} & \cdots & \frac{\partial y_m}{\partial x_{n}} \\
\end{matrix}
\right
)_{(m,n)m\times n}
\]
例五
\[\mathbfcal{x}=
\left[
\begin {array}{1}
x_1 \\
x_2
\end{array}
\right ]_{(2,1)2 \times 1}
\\
\mathbfcal{y}=\mathbfcal{f}(x)=
\left[
\begin {array}{1}
x_1+x_2 \\
2x_1^2+2x_2^2 \\
3x_1^3+3x_2^3
\end{array}
\right ]_{(3,1)3 \times 1} \\
\mathbfcal{f}'(x)=\frac{\partial \mathbfcal{y}}{ \partial x} =
\left[
\begin {array}{1}
1 &1 \\
4x_1 &4x_2 \\
9x_1^2 &9x_3^2
\end{array}
\right ]_{(3,2)3\times 2}
\]
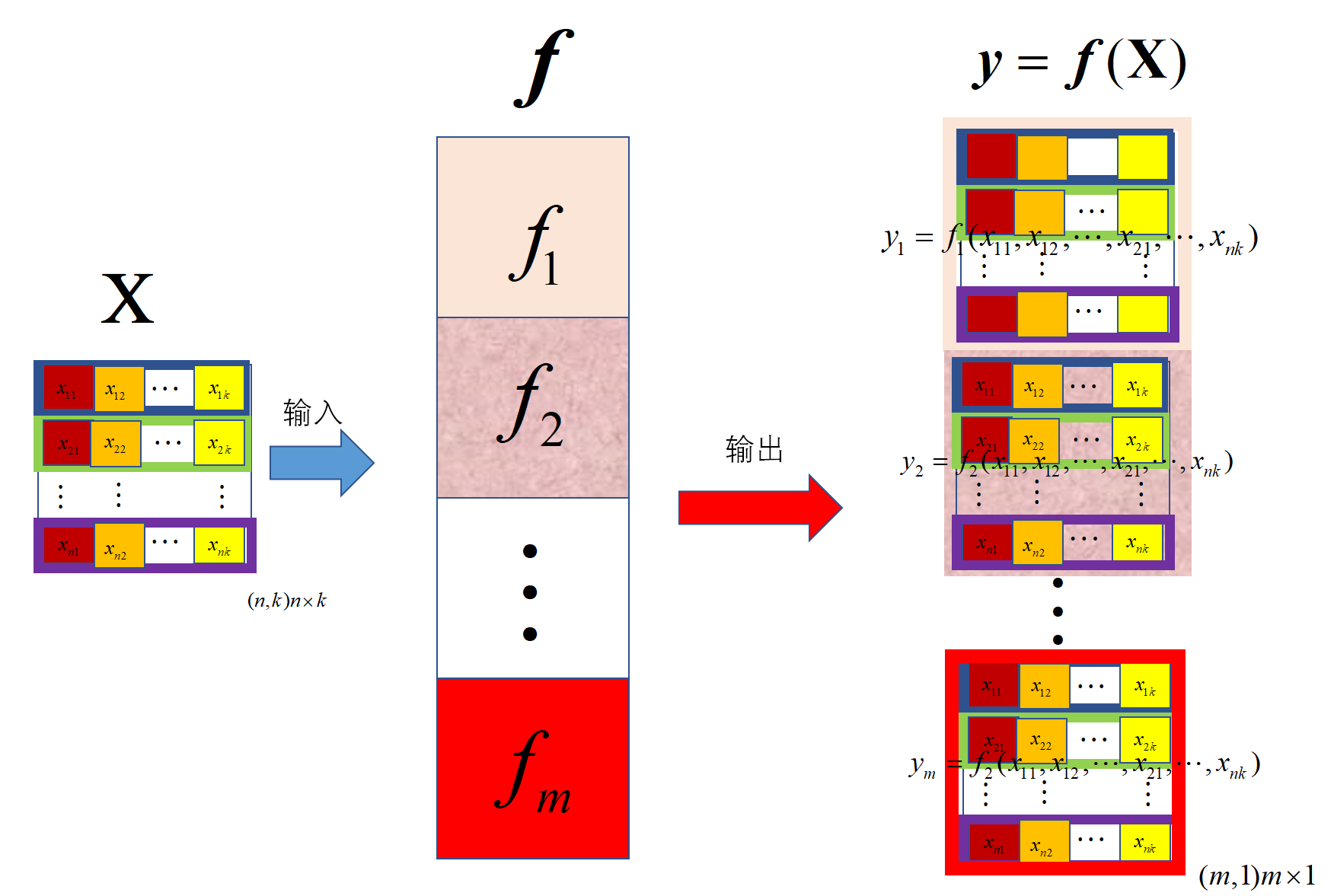
2.3 \(\text{input}\)是一个矩阵
计算:输入(变元)是矩阵(\((n,k)n\times k\)),函数是列向量函数(\((m,1)m \times 1\)),输出结果是列向量(\((m,1)m \times 1\))
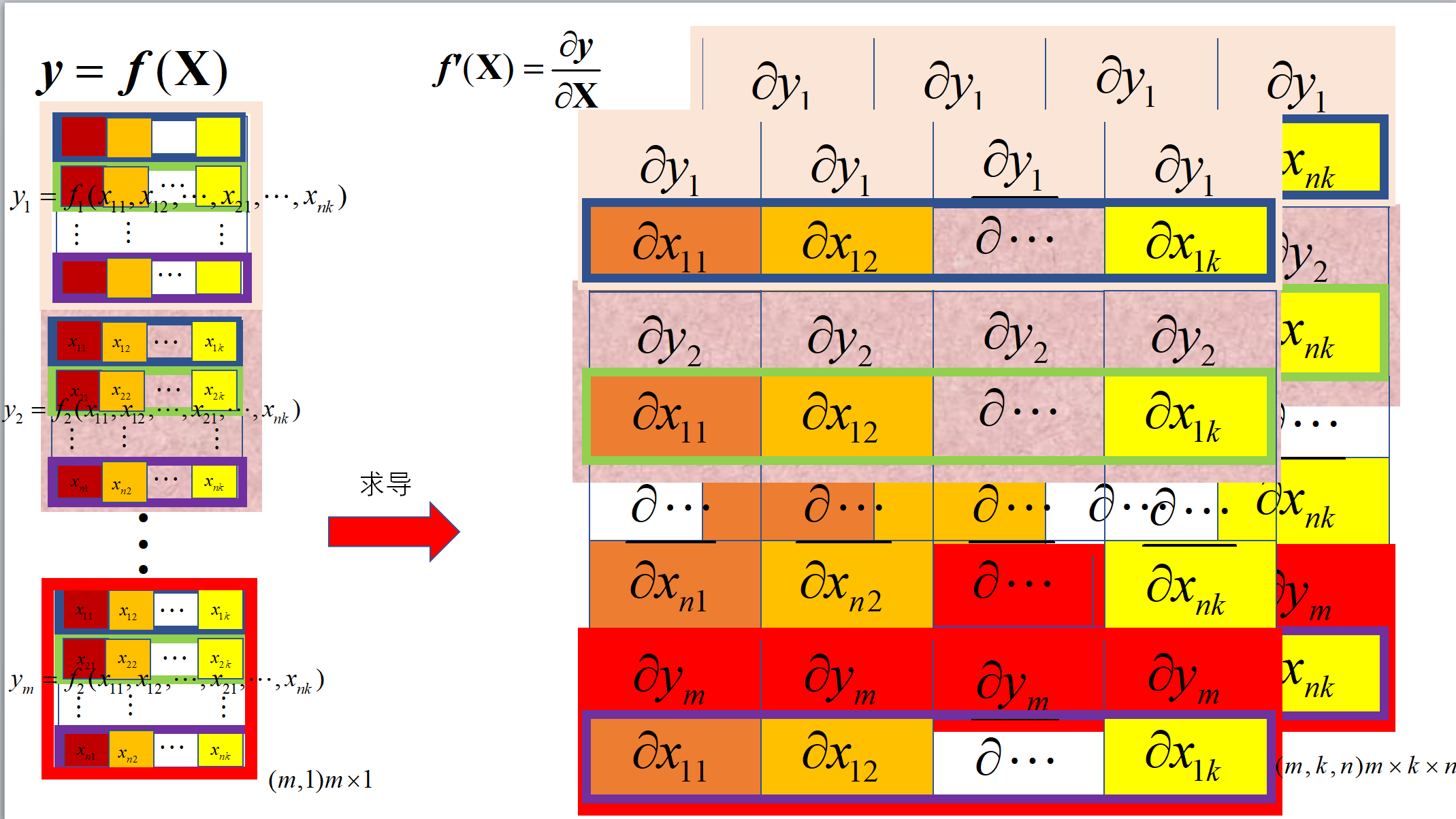
求导: 求导分母(函数值)是列向量(\((m,1)m \times 1\)),分子是矩阵(\((n,k) n \times k\)),求导结果是张量(\((m,k,n)m \times k \times n\))
\[\symbf{X} =
\left (
\begin{matrix}
x_{11} & x_{12} & \cdots & x_{1k} \\
x_{21} & x_{22} & \cdots & x_{2k} \\
\vdots & \vdots & & \vdots \\
x_{n1} & x_{n2} & \cdots & x_{nk} \\
\end{matrix}
\right
)_{(n,k)n\times k} \\
\\
\mathbfcal{y} = \mathbfcal{f}(\symbf{X})=
\left[
\begin {array}{1}
y_1 \\
y_2 \\
\vdots \\
y_m
\end{array}
\right ]
=
\left[
\begin {array}{1}
f_1(x_{11},x_{12},\cdots,x_{21},\cdots,x_{nn}) \\
f_2(x_{11},x_{12},\cdots,x_{21},\cdots,x_{nn}) \\
\vdots \\
f_m(x_{11},x_{12},\cdots,x_{21},\cdots,x_{nn})
\end{array}
\right ]_{(m,1)m\times 1}
\\
\frac{\partial \mathbfcal{y}}{ \partial \symbf{X}} =
\left (
\begin{matrix}
\frac{\partial y_1}{\partial x_{11}} & \frac{\partial y_1}{\partial x_{12}} & \cdots & \frac{\partial y_1}{\partial x_{1k}} \\
\frac{\partial y_2}{\partial x_{11}} & \frac{\partial y_2}{\partial x_{12}} & \cdots & \frac{\partial y_2}{\partial x_{1k}} \\
\vdots & \vdots & & \vdots \\
\frac{\partial y_m}{\partial x_{11}} & \frac{\partial y_m}{\partial x_{12}} & \cdots & \frac{\partial y_m}{\partial x_{1k}} \\
\end{matrix}
\right
)
\left (
\begin{matrix}
\frac{\partial y_1}{\partial x_{21}} & \frac{\partial y_1}{\partial x_{22}} & \cdots & \frac{\partial y_1}{\partial x_{2k}} \\
\frac{\partial y_2}{\partial x_{21}} & \frac{\partial y_2}{\partial x_{22}} & \cdots & \frac{\partial y_2}{\partial x_{2k}} \\
\vdots & \vdots & & \vdots \\
\frac{\partial y_m}{\partial x_{21}} & \frac{\partial y_m}{\partial x_{22}} & \cdots & \frac{\partial y_m}{\partial x_{2k}} \\
\end{matrix}
\right
)
\cdots
\left (
\begin{matrix}
\frac{\partial y_1}{\partial x_{n1}} & \frac{\partial y_1}{\partial x_{n2}} & \cdots & \frac{\partial y_1}{\partial x_{nk}} \\
\frac{\partial y_2}{\partial x_{n1}} & \frac{\partial y_2}{\partial x_{n2}} & \cdots & \frac{\partial y_2}{\partial x_{nk}} \\
\vdots & \vdots & & \vdots \\
\frac{\partial y_m}{\partial x_{n1}} & \frac{\partial y_m}{\partial x_{n2}} & \cdots & \frac{\partial y_m}{\partial x_{nk}} \\
\end{matrix}
\right
)
_{(m,k,n)m\times k\times n}
\]
3 \(\text{function}\)是一个矩阵
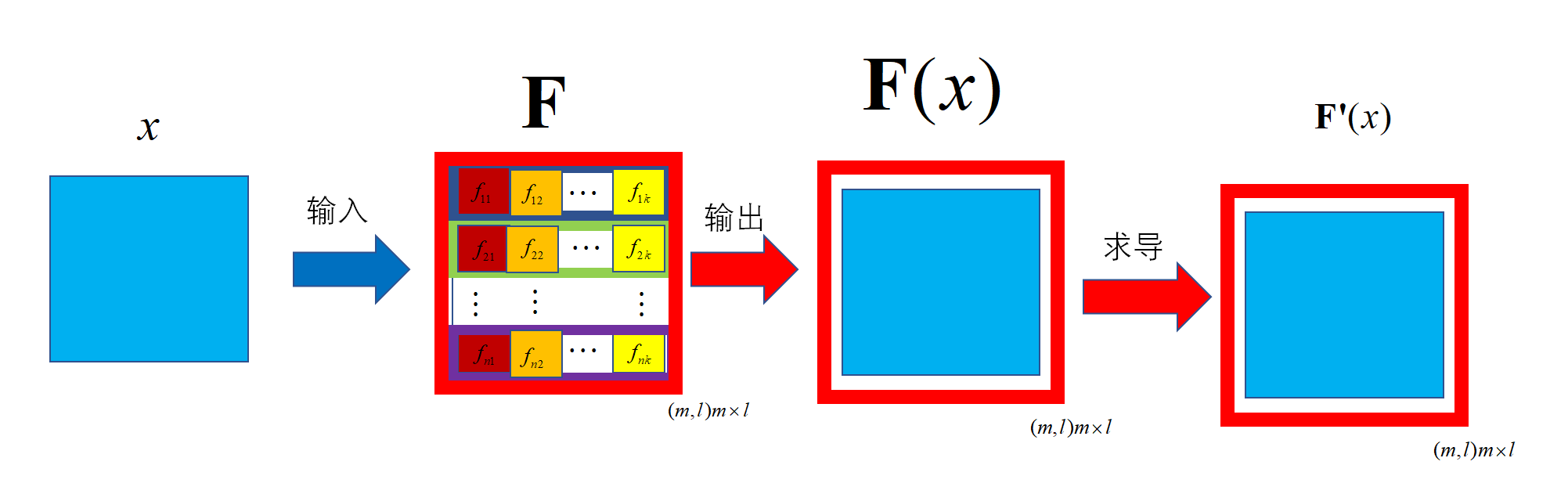
我们称\(\text{function}\)是一个实矩阵函数。用粗体大写字母\(\mathbf{F}\)表示。
含义: \(\mathbf{F}\)是由 若干个\(f\)组成的一个矩阵
3.1 \(\text{input}\)是一个标量
计算:输入是标量(\((1,)\)),函数是一个实矩阵函数,结果是一个矩阵(\((m,l)\))
求导: 分母(函数值)是矩阵(\((m,l)\)),分子是标量(\((1,)\)),结果是矩阵(\((m,l)\))
\[x \\
\symbf{Y} = \mathbf{F}(x)=
\left (
\begin{matrix}
f_{11}(x) & f_{12}(x) & \cdots & f_{1l}(x) \\
f_{21}(x) & f_{22}(x) & \cdots & f_{2l}(x) \\
\vdots & \vdots & & \vdots \\
f_{m1}(x) & f_{m2}(x) & \cdots & f_{ml}(x) \\
\end{matrix}
\right
)
=
\left (
\begin{matrix}
y_{11} & y_{12} & \cdots & y_{1l} \\
y_{21} & y_{22} & \cdots & y_{2l} \\
\vdots & \vdots & & \vdots \\
y_{m1} & y_{m2} & \cdots & y_{ml} \\
\end{matrix}
\right
)_{(m,l)m\times l}
\\
\frac{ \partial\symbf{Y}}{\partial x} =\mathbf{F}'(x) =
\left (
\begin{matrix}
f'_{11}(x) & f'_{12}(x) & \cdots & f'_{1l}(x) \\
f'_{21}(x) & f'_{22}(x) & \cdots & f'_{2l}(x) \\
\vdots & \vdots & & \vdots \\
f'_{m1}(x) & f'_{m2}(x) & \cdots & f'_{ml}(x) \\
\end{matrix}
\right
)
=
\left (
\begin{matrix}
\frac{ \partial y_{11}}{ \partial x} & \frac{ \partial y_{12}}{ \partial x} & \cdots & \frac{ \partial y_{1l}}{ \partial x} \\
\frac{ \partial y_{21}}{ \partial x} & \frac{ \partial y_{22}}{ \partial x} & \cdots & \frac{ \partial y_{2l}}{ \partial x} \\
\vdots & \vdots & & \vdots \\
\frac{ \partial y_{m1}}{ \partial x} & \frac{ \partial y_{m2}}{ \partial x} & \cdots & \frac{ \partial y_{ml}}{ \partial x} \\
\end{matrix}
\right
)_{(m,l)m\times l}
\]
3.2 \(\text{input}\)是一个向量
计算:输入是向量(\((n,1)\)),函数是一个实矩阵函数,结果是一个矩阵(\((m,l)\))
求导: 分母(函数值)是矩阵(\((m,l)\)),分子是向量(\((n,1)\)),结果是矩阵(\((m,l,n)m\times l \times n\))
3.3 \(\text{input}\)是一个矩阵
计算:输入是矩阵(\((n,k)\)),函数是一个实矩阵函数,结果是一个矩阵(\((m,l)\))
求导: 分母(函数值)是矩阵(\((m,l)\)),分子是矩阵(\((n,k)\)),结果是矩阵(\((m,l,k,n)m\times l \times k \times n\))
总结


样例
标量关于向量求导1.2

向量关于向量求导2.2

二 向量链式法则

标量链式法则
\(x,u,y\)都是标量
\[y=f(u) , u=g(x) \\
\frac{\partial y}{\partial x} = \frac{\partial y}{\partial u}\frac{\partial u}{\partial x}
\]
向量链式法则
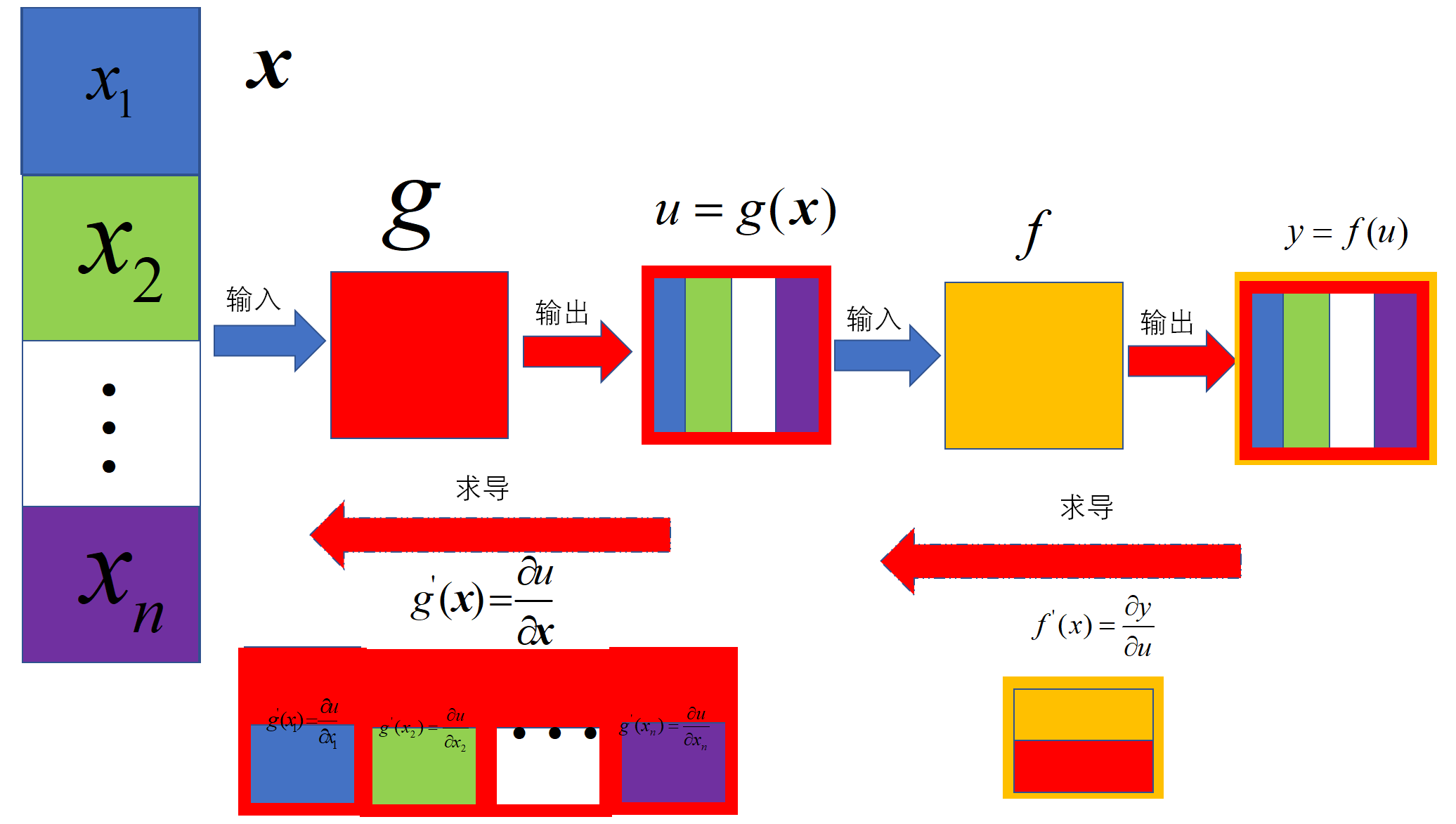
标量关于向量求导
-
中间变量是标量 1.1 1.2
\[y=f(u) , u=g(\mathbfcal{x}) \\
\mathbfcal{x}_{(n,1)}、u_{(1,)}、y_{(1,)} \\
\frac{\partial y}{\partial \mathbfcal{x}}_{(1,n)} = \frac{\partial y}{\partial u}_{(1,)} \frac{\partial u}{\partial \mathbfcal{x}}_{(1,n)}
\]
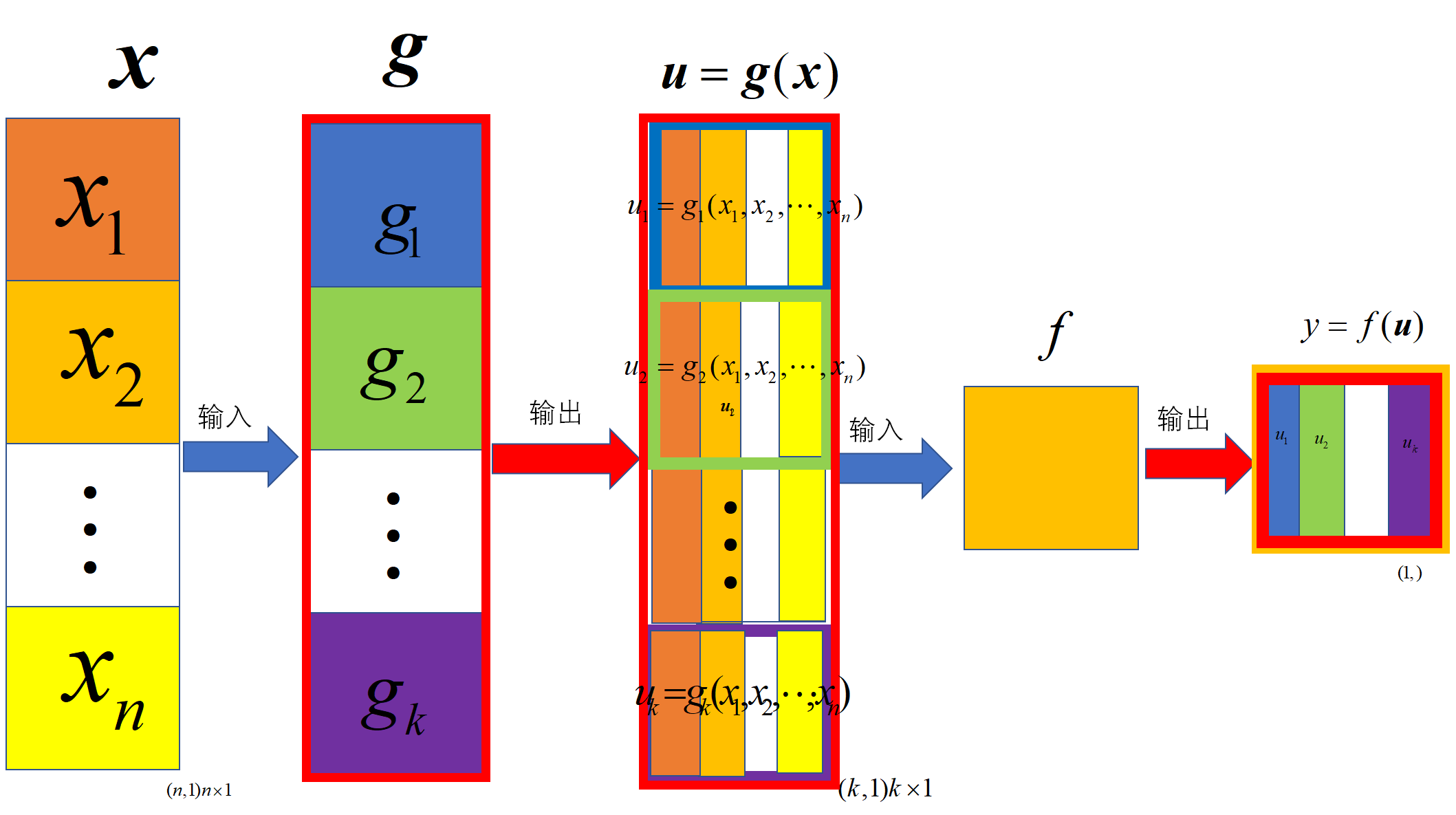
-
中间变量是向量 1.2 , 2.2
\[y=f(\mathbfcal{u}) , \mathbfcal{u}_{(k,1)}=\mathbfcal{g}(\mathbfcal{x}) \\
\mathbfcal{x}_{(n,1)}、\mathbfcal{u}_{(k,1)}、y_{(1,)} \\
\frac{\partial y}{\partial \mathbfcal{x}}_{(1,n)} = \frac{\partial y}{\partial \mathbfcal{u}}_{(1,k)} \frac{\partial \mathbfcal{u}}{\partial \mathbfcal{x}}_{(k,n)}
\]
向量关于向量求导
- 中间变量是向量 2.2 2.2
\[\mathbfcal{y}_{(m,1)}=\mathbfcal{f}_{(m,1)}(\mathbfcal{u}_{(k,1)}) , \mathbfcal{u}_{(k,1)}=\mathbfcal{g}_{(k,1)}(\mathbfcal{x}_{(n,1)}) \\
\mathbfcal{x}_{(n,1)}、\mathbfcal{u}_{(k,1)}、\mathbfcal{y}_{(m,1)} \\
\frac{\partial \mathbfcal{y}}{\partial \mathbfcal{x}}_{(m,n)} = \frac{\partial \mathbfcal{y}}{\partial \mathbfcal{u}}_{(m,k)} \frac{\partial \mathbfcal{u}}{\partial \mathbfcal{x}}_{(k,n)}
\]
样例

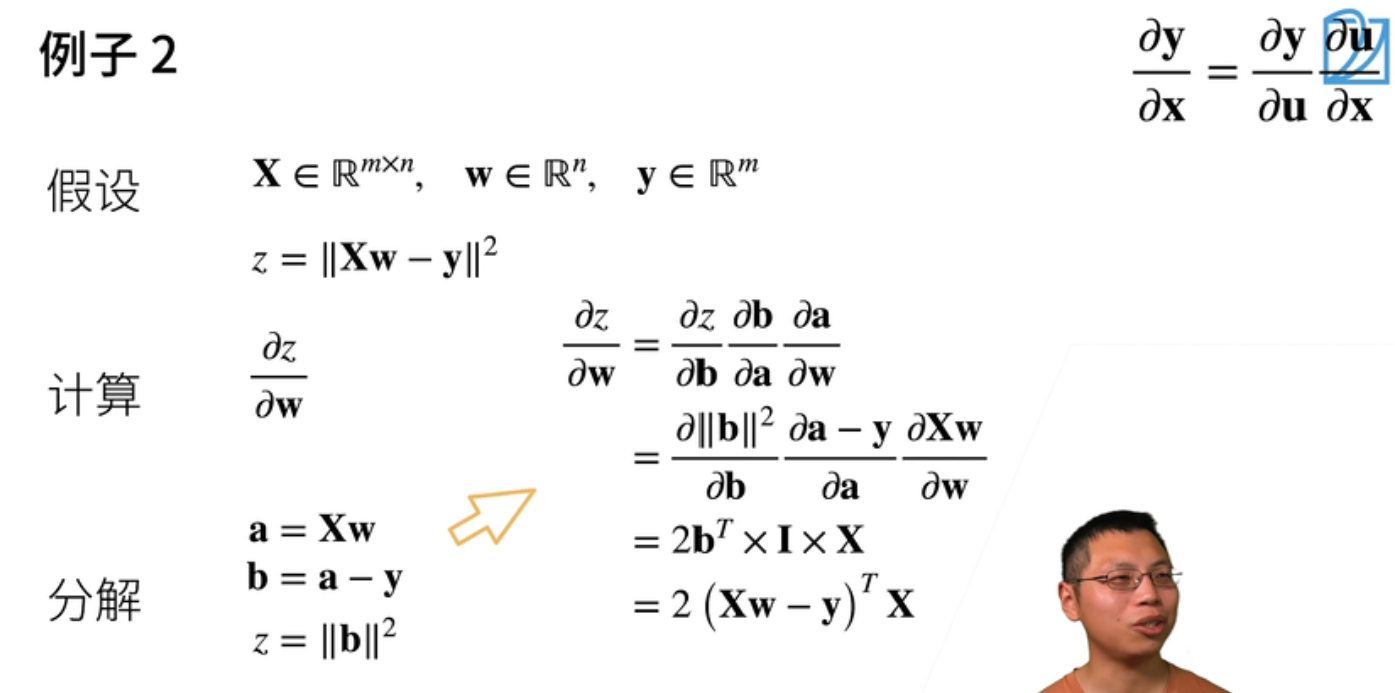
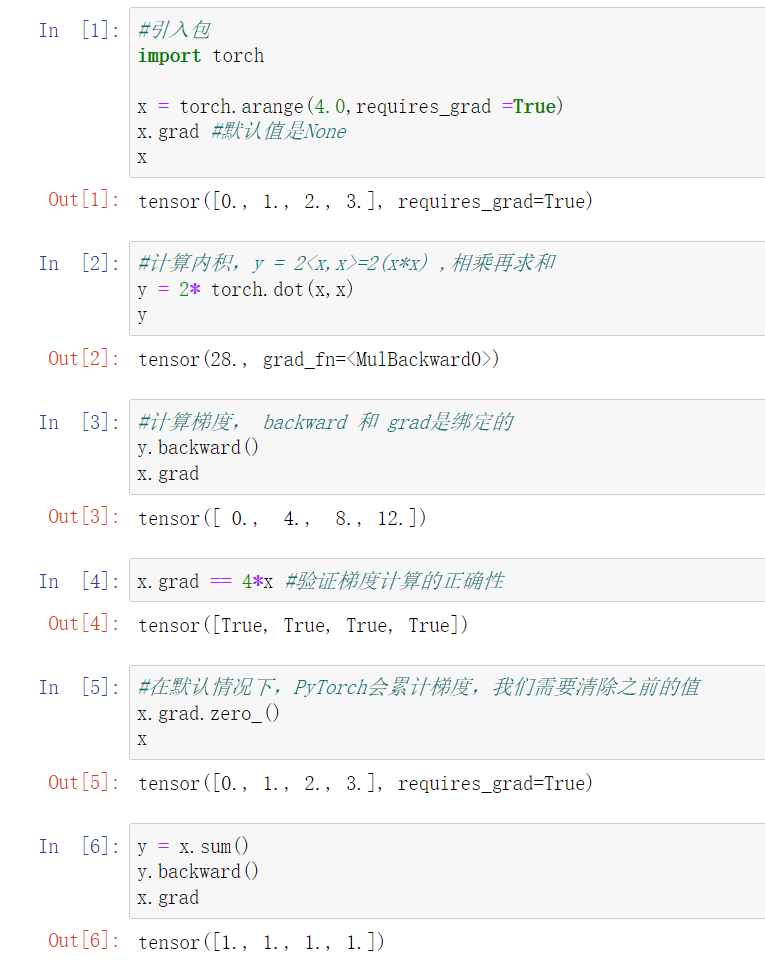
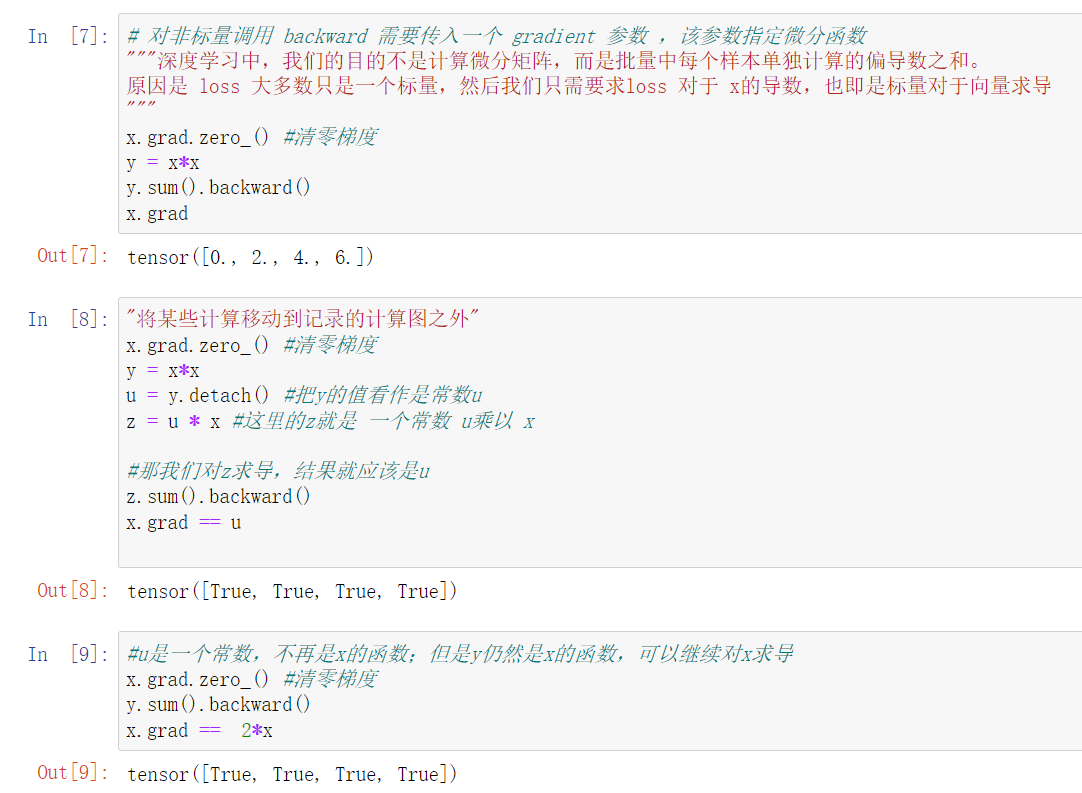
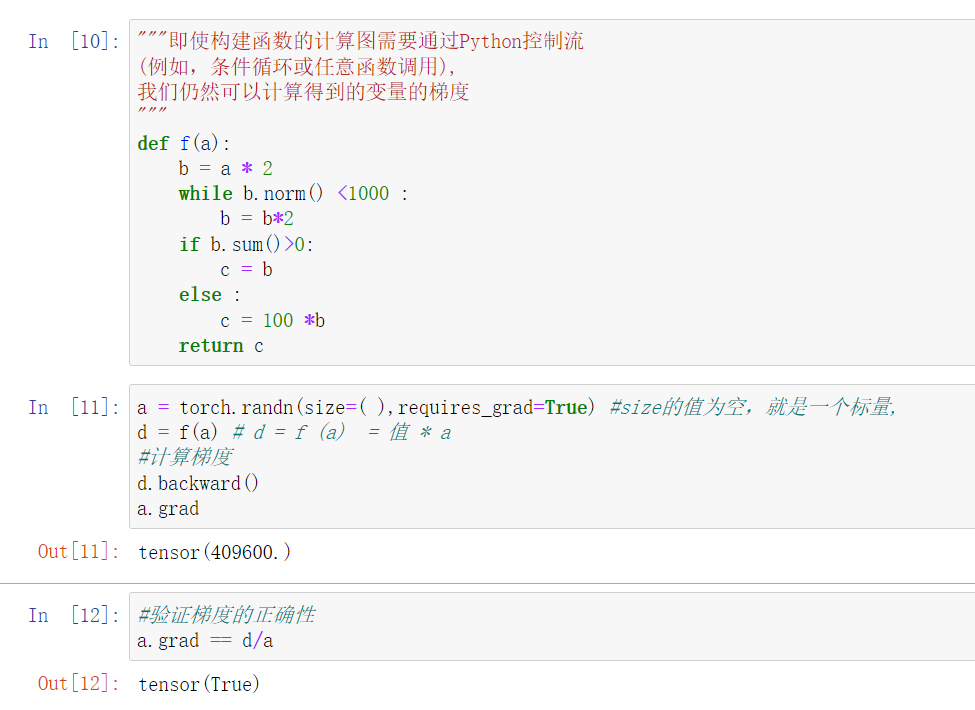
三 自动求导

自动求导,是求导计算一个函数在指定值上的导数
计算图
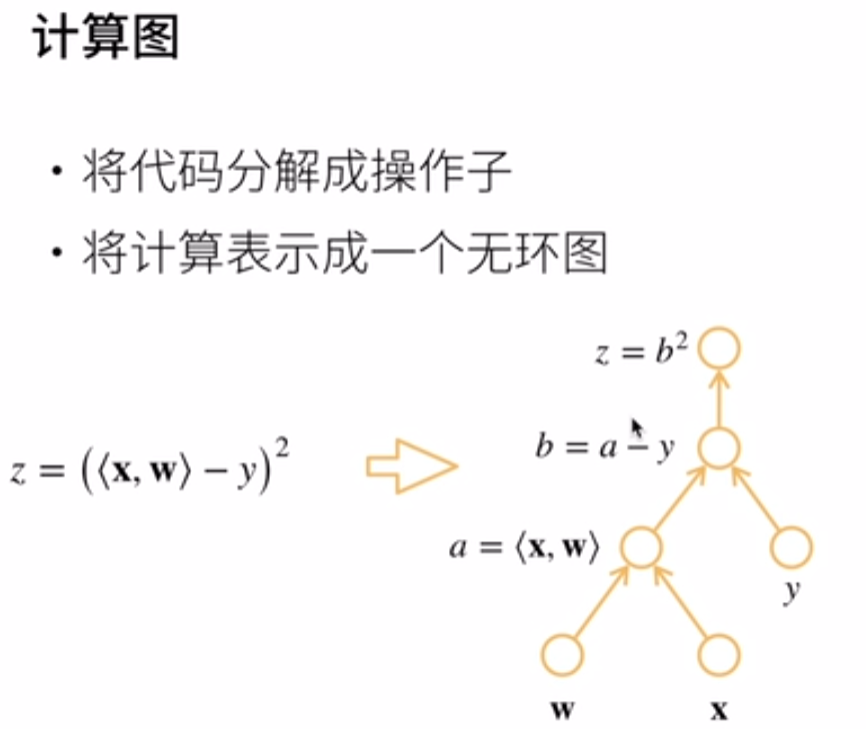
两种模式

反向累积
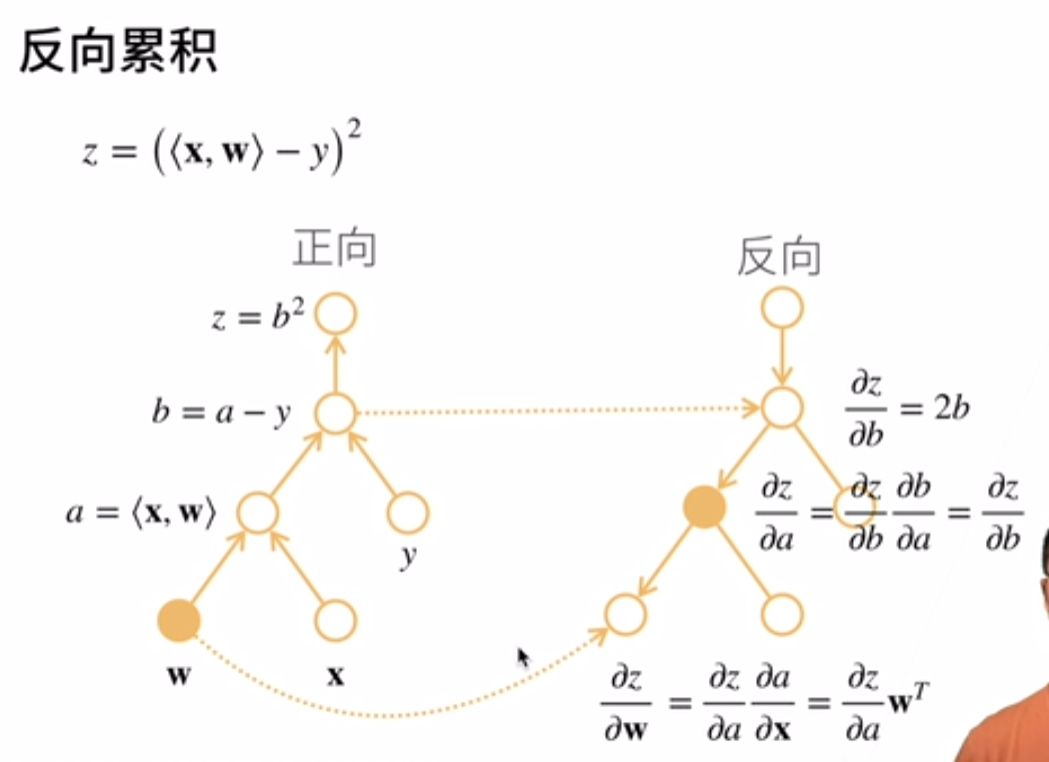
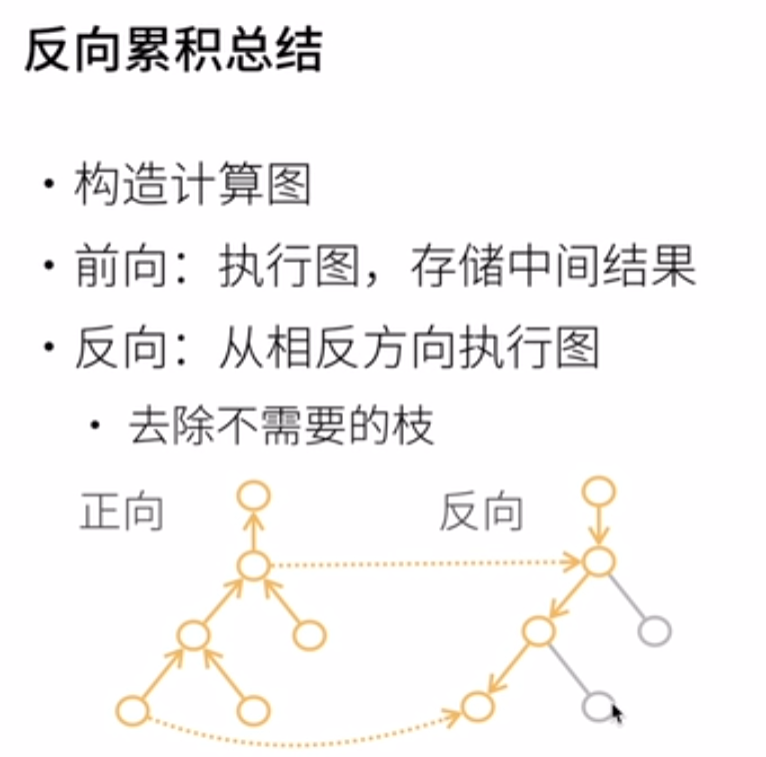
复杂度

代码实现