平衡二叉搜索树(Self-balancing binary search tree)又被称为AVL树(有别于AVL算法),且具有以下性质:它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树,同时,平衡二叉树必定是二叉排序树。
高度差可以用平衡因子bf来定义,我们用左子树的高度减去右子树的高度来表示bf,即-1<|bf|<1。
引入平衡二叉树是由于二叉排序树,在某些情况会导致树的高度一直的增加,比如一组有序的数据,在查找或创建时递归层级会很深,导致方法栈容易溢出。
平衡二叉树是通过旋转来缓解树高度增加过快的情况。
先介绍下最小不平衡节点的概念:插入一个节点之后,距离这个插入节点最近的不平衡节点就是最小不平衡节点。就是说在递归插入节点后,开始回溯,碰到的第一个不平衡的节点就是最小不平衡节点。
当最小不平衡节点右子树高则需要左旋,左子树高则需要右旋(还有些情况需要先对其左/右子树旋转)。
思考:
1、既然旋转是通过平衡因子|bf|>1来决定怎么旋转的,那么在旋转前这些平衡因子是什么时候赋值的呢?
2、旋转之后,哪些节点需要调整?,平衡因子又改如何调整呢?
下图只列出左子树高的几种情况,T表示最小不平衡节点,L表示其左子树,LR表示L的右子树,
为了形象用EH(0),LH(1),RH(-1)分别表示某一节点 左右子树相等、左子树高、右子树高三种情况。
根据L节点的左右子树高度差来确定直接右旋还是先左旋再右旋,因为L为最小不平衡子树的左子树,故不会出现L.bf=EH的情况。
一、L.bf=LH
右旋:
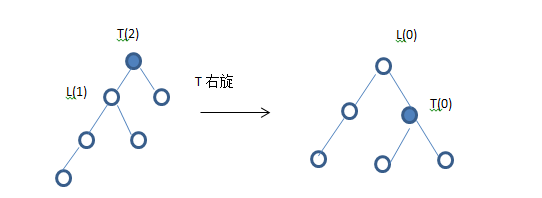
旋转之后T.bf=L.bf=EH
二、L.bf=RH
先左旋再右旋:
当L的平衡因子为-1时则需要先对L进行右旋,然后再对T进行左旋。根据LR的情况再分为下面三种(因为旋转两次,那么最后最小不平衡子树的根节点为LR,并且LR.bf=EH)
1、 LR=EH

旋转之后T.bf=L.bf=EH
2、 LR=LH

旋转之后T.bf=RH, L.bf=EH
3、 LR=RH

旋转之后T.bf=EH, L.bf=LH
我认为网上最容易懂的C语言版代码入下:
1. #include "stdio.h"
2. #include "stdlib.h"
3. #include "io.h"
4. #include "math.h"
5. #include "time.h"
6.
7. #define OK 1
8. #define ERROR 0
9. #define TRUE 1
10. #define FALSE 0
11. #define MAXSIZE 100 /* 存储空间初始分配量 */
12.
13. typedef int Status; /* Status是函数的类型,其值是函数结果状态代码,如OK等 */
14.
15.
16. /* 二叉树的二叉链表结点结构定义 */
17. typedef struct BiTNode /* 结点结构 */
18. {
19. int data; /* 结点数据 */
20. int bf; /* 结点的平衡因子 */
21. struct BiTNode *lchild, *rchild; /* 左右孩子指针 */
22. } BiTNode, *BiTree;
23.
24.
25. /* 对以p为根的二叉排序树作右旋处理, */
26. /* 处理之后p指向新的树根结点,即旋转处理之前的左子树的根结点 */
27. void R_Rotate(BiTree *P)
28. {
29. BiTree L;
30. L=(*P)->lchild; /* L指向P的左子树根结点 */
31. (*P)->lchild=L->rchild; /* L的右子树挂接为P的左子树 */
32. L->rchild=(*P);
33. *P=L; /* P指向新的根结点 */
34. }
35.
36. /* 对以P为根的二叉排序树作左旋处理, */
37. /* 处理之后P指向新的树根结点,即旋转处理之前的右子树的根结点0 */
38. void L_Rotate(BiTree *P)
39. {
40. BiTree R;
41. R=(*P)->rchild; /* R指向P的右子树根结点 */
42. (*P)->rchild=R->lchild; /* R的左子树挂接为P的右子树 */
43. R->lchild=(*P);
44. *P=R; /* P指向新的根结点 */
45. }
46.
47. #define LH +1 /* 左高 */
48. #define EH 0 /* 等高 */
49. #define RH -1 /* 右高 */
50.
51. /* 对以指针T所指结点为根的二叉树作左平衡旋转处理 */
52. /* 本算法结束时,指针T指向新的根结点 */
53. void LeftBalance(BiTree *T)
54. {
55. BiTree L,Lr;
56. L=(*T)->lchild; /* L指向T的左子树根结点 */
57. switch(L->bf)
58. { /* 检查T的左子树的平衡度,并作相应平衡处理 */
59. case LH: /* 新结点插入在T的左孩子的左子树上,要作单右旋处理 */
60. (*T)->bf=L->bf=EH;
61. R_Rotate(T);
62. break;
63. case RH: /* 新结点插入在T的左孩子的右子树上,要作双旋处理 */
64. Lr=L->rchild; /* Lr指向T的左孩子的右子树根 */
65. switch(Lr->bf)
66. { /* 修改T及其左孩子的平衡因子 */
67. case LH: (*T)->bf=RH;
68. L->bf=EH;
69. break;
70. case EH: (*T)->bf=L->bf=EH;
71. break;
72. case RH: (*T)->bf=EH;
73. L->bf=LH;
74. break;
75. }
76. Lr->bf=EH;
77. L_Rotate(&(*T)->lchild); /* 对T的左子树作左旋平衡处理 */
78. R_Rotate(T); /* 对T作右旋平衡处理 */
79. }
80. }
81.
82. /* 对以指针T所指结点为根的二叉树作右平衡旋转处理, */
83. /* 本算法结束时,指针T指向新的根结点 */
84. void RightBalance(BiTree *T)
85. {
86. BiTree R,Rl;
87. R=(*T)->rchild; /* R指向T的右子树根结点 */
88. switch(R->bf)
89. { /* 检查T的右子树的平衡度,并作相应平衡处理 */
90. case RH: /* 新结点插入在T的右孩子的右子树上,要作单左旋处理 */
91. (*T)->bf=R->bf=EH;
92. L_Rotate(T);
93. break;
94. case LH: /* 新结点插入在T的右孩子的左子树上,要作双旋处理 */
95. Rl=R->lchild; /* Rl指向T的右孩子的左子树根 */
96. switch(Rl->bf)
97. { /* 修改T及其右孩子的平衡因子 */
98. case RH: (*T)->bf=LH;
99. R->bf=EH;
100. break;
101. case EH: (*T)->bf=R->bf=EH;
102. break;
103. case LH: (*T)->bf=EH;
104. R->bf=RH;
105. break;
106. }
107. Rl->bf=EH;
108. R_Rotate(&(*T)->rchild); /* 对T的右子树作右旋平衡处理 */
109. L_Rotate(T); /* 对T作左旋平衡处理 */
110. }
111. }
112.
113. /* 若在平衡的二叉排序树T中不存在和e有相同关键字的结点,则插入一个 */
114. /* 数据元素为e的新结点,并返回1,否则返回0。若因插入而使二叉排序树 */
115. /* 失去平衡,则作平衡旋转处理,布尔变量taller反映T长高与否。 */
116. Status InsertAVL(BiTree *T,int e,Status *taller)
117. {
118. if(!*T)
119. { /* 插入新结点,树“长高”,置taller为TRUE */
120. *T=(BiTree)malloc(sizeof(BiTNode));
121. (*T)->data=e; (*T)->lchild=(*T)->rchild=NULL; (*T)->bf=EH;
122. *taller=TRUE;
123. }
124. else
125. {
126. if (e==(*T)->data)
127. { /* 树中已存在和e有相同关键字的结点则不再插入 */
128. *taller=FALSE; return FALSE;
129. }
130. if (e<(*T)->data)
131. { /* 应继续在T的左子树中进行搜索 */
132. if(!InsertAVL(&(*T)->lchild,e,taller)) /* 未插入 */
133. return FALSE;
134. if(*taller) /* 已插入到T的左子树中且左子树“长高” */
135. switch((*T)->bf) /* 检查T的平衡度 */
136. {
137. case LH: /* 原本左子树比右子树高,需要作左平衡处理 */
138. LeftBalance(T); *taller=FALSE; break;
139. case EH: /* 原本左、右子树等高,现因左子树增高而使树增高 */
140. (*T)->bf=LH; *taller=TRUE; break;
141. case RH: /* 原本右子树比左子树高,现左、右子树等高 */
142. (*T)->bf=EH; *taller=FALSE; break;
143. }
144. }
145. else
146. { /* 应继续在T的右子树中进行搜索 */
147. if(!InsertAVL(&(*T)->rchild,e,taller)) /* 未插入 */
148. return FALSE;
149. if(*taller) /* 已插入到T的右子树且右子树“长高” */
150. switch((*T)->bf) /* 检查T的平衡度 */
151. {
152. case LH: /* 原本左子树比右子树高,现左、右子树等高 */
153. (*T)->bf=EH; *taller=FALSE; break;
154. case EH: /* 原本左、右子树等高,现因右子树增高而使树增高 */
155. (*T)->bf=RH; *taller=TRUE; break;
156. case RH: /* 原本右子树比左子树高,需要作右平衡处理 */
157. RightBalance(T); *taller=FALSE; break;
158. }
159. }
160. }
161. return TRUE;
162. }
163.
164. int main(void)
165. {
166. int i;
167. int a[10]={3,2,1,4,5,6,7,10,9,8};
168. BiTree T=NULL;
169. Status taller;
170. for(i=0;i<10;i++)
171. {
172. InsertAVL(&T,a[i],&taller);
173. }
174. printf("本样例建议断点跟踪查看平衡二叉树结构");
175. return 0;
176. }
首先整体看一遍InsertAVL函数代码,结合上面的图,我想之前两个问题都会有答案了,再重复下。
1、既然旋转是通过平衡因子|bf|>1来决定怎么旋转的,那么在旋转前这些平衡因子是什么时候赋值呢?
在元素插入之后,首先认为该元素就是一个子树,从无到有,故高度增加taller=true,然后开始回溯到上一个节点根据元素插入后,对其的三种影响来调整平衡因子,同时重新赋值taller。
2、旋转之后,哪些节点需要调整?平衡因子又改如何调整呢?
因为平衡二叉树本身也是排序树,就上图以左子树高为列,若能直接右旋,影响的节点有T、L,最后会为T.bf=L.bf=EH。
若要先左旋再右旋,则根据LR的取值再分三种情况(最后会变成LR为根,LR.bf=EH)
1、 LR.bf=EH:旋转后 T.bf=L.bf=EH
2、 LR.bf=LH:旋转后 T.bf=RH,L.bf=EH
3、 LR.bf=RH:旋转后 T.bf=EH,L.bf=LH
右子树高的情况同理。
要是你对java实现不兴趣,可以不用往下看了,数据结构主要是其思想,实现只需要根据语言特性来稍作改变。
java代码:
思路跟上面代码一样(原谅我偷懒不写注释...),主要是多了个rootAVL和preNode。原因是c语言函数传值可以直接传指针,这样对于参数的修改会反应到被调函数外面。而java都是值传递,方法内操作的只是引用的一个副本,他们指向的地址相同而已,只能修改引用所指向的内存,修改引用副本是不会影响引用本身的。
故需要单独处理节点的前驱和根节点, rootAVL用来保存最后的根节点,因为每次插入都需要从根节点开始递归。
preNode表示每次回溯时的前面一个节点。
public class AVL { private boolean taller=false; private Node root =null; private static final int EH=0; private static final int LH=1; private static final int RH=-1; private class Node{ public int data; public Node leftChild; public Node rightChild; public int balanceFactor; public Node(int data){ this.data=data; balanceFactor=0; } } public Node RRotate(Node T){ Node temp=T.leftChild; T.leftChild=temp.rightChild; temp.rightChild=T; return temp; } public Node LRotate(Node T){ Node temp=T.rightChild; T.rightChild=temp.leftChild; temp.leftChild=T; return temp; } public Node leftBalance(Node node,Node preNode){ Node child=node.leftChild; Node root=null; switch (child.balanceFactor){ case LH: node.balanceFactor=child.balanceFactor=EH; root=RRotate(node); if(preNode!=null && node.data< preNode.data){ preNode.leftChild=root; } if(preNode!=null && node.data> preNode.data){ preNode.rightChild=root; } break; case RH: Node rchild=child.rightChild; switch (rchild.balanceFactor){ case EH: node.balanceFactor=child.balanceFactor=EH; break; case LH: node.balanceFactor=RH; child.balanceFactor=EH; break; case RH: node.balanceFactor=EH; child.balanceFactor=LH; break; default:break; } rchild.balanceFactor=EH; node.leftChild=LRotate(child); root=RRotate(node); if(preNode!=null && node.data<preNode.data){ preNode.leftChild=root; } if(preNode!=null && node.data>preNode.data){ preNode.rightChild=root; } break; default:break; } return root; } public Node rightBalance(Node node,Node preNode){ Node child=node.rightChild; Node root=null; switch (child.balanceFactor){ case RH: node.balanceFactor=child.balanceFactor=EH; root=LRotate(node); if(preNode!=null && node.data<preNode.data){ preNode.leftChild=root; } if(preNode!=null && node.data>preNode.data){ preNode.rightChild=root; } break; case LH: Node lchild=child.leftChild; switch (lchild.balanceFactor){ case EH: node.balanceFactor=child.balanceFactor=EH; break; case RH: node.balanceFactor=LH; child.balanceFactor=EH; break; case LH: node.balanceFactor=EH; child.balanceFactor=RH; break; default:break; } lchild.balanceFactor=EH; node.rightChild=RRotate(child); root=LRotate(node); if(preNode!=null && node.data<preNode.data){ preNode.leftChild=root; } if( preNode!=null && node.data>preNode.data){ preNode.rightChild=root; } break; default:break; } return root; } public boolean insertNode(int value){ return insertNode(root,value,null); } public boolean insertNode(Node node, int value, Node preNode){ if(node==null){ node=new Node(value); node.balanceFactor=EH; taller=true; if(preNode!=null && node.data< preNode.data){ preNode.leftChild=node; } if(preNode!=null && node.data> preNode.data){ preNode.rightChild=node; } root =node; return true; }else{ if(value==node.data){ root =node; return false; } if (value<node.data){ if (!insertNode(node.leftChild, value, node)) { root =node; return false; } if(taller){ switch (node.balanceFactor){ case EH:taller=true;node.balanceFactor=LH;break; case RH:taller=false;node.balanceFactor=EH;break; case LH: taller=false; node=leftBalance(node,preNode); if(preNode!=null){ node=preNode; } break; default:break; } } } if (value>node.data){ if (!insertNode(node.rightChild, value,node)) { root =node; return false; } if(taller){ switch (node.balanceFactor){ case EH:taller=true;node.balanceFactor=RH;break; case LH:taller=false;node.balanceFactor=EH;break; case RH: taller=false; node=rightBalance(node,preNode); if(preNode!=null){ node=preNode; } break; default:break; } } } } root =node; return true; } public void inorderTraversal(){ inorderTraversal(root); } public void inorderTraversal(Node root){ if(root!=null){ inorderTraversal(root.leftChild); System.out.println("节点:"+root.data+" 平衡因子:"+root.balanceFactor); inorderTraversal(root.rightChild); } return ; } public static void main(String[] args) { //int[] data={8,6,4}; //int[] data={8,6,9,5,7,3}; //int[] data={8,6,7}; //int[] data={8,5,9,4,6,7}; //int[] data={8,5,9,4,7,6}; int[] data={8,5,9,7,6}; AVL avl=new AVL(); for(int i=0;i<data.length;i++){ avl.insertNode(data[i]); } avl.inorderTraversal(); } }