题目描述
萨丽·斯内尔(Sally Snail,蜗牛)喜欢在N x N 的棋盘上闲逛(1 < n <= 120)。
她总是从棋盘的左上角出发。棋盘上有空的格子(用“.”来表示)和B 个路障(用“#”来表示)。
下面是这种表示法的示例棋盘:

萨丽总是垂直(向上或者向下)或水平(向左或者向右)地走。她可以从出发地(总是记作A1 )向下或者向右走。一旦萨丽选定了一个方向,她就会一直走下去。如果她遇到棋盘边缘或者路障,她就停下来,并且转过90 度。她不可能离开棋盘,或者走进路障当中。并且,萨丽从不跨过她已经经过的格子。当她再也不能走的时候,她就停止散步。
这里是上面的棋盘上的一次散步路线图示:
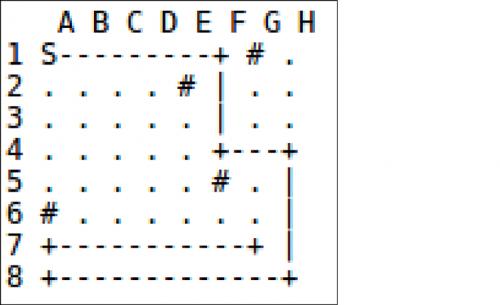
萨丽向右走,再向下,向右,向下,然后向左,再向上,最后向右走。这时她遇到了一个她已经走过的格子,她就停下来了。但是,如果她在F5 格遇到路障后选择另外一条路——向我们看来是左边的方向转弯,情况就不一样了。
你的任务是计算并输出,如果萨丽聪明地选择她的路线的话,她所能够经过的最多格子数。
输入输出格式
输入格式:
输入的第一行包括N —棋盘的大小,和B —路障的数量(1 <= B <= 200)。接下来的B 行包含着路障的位置信息。下面的样例输入对应着上面的示例棋盘。下面的输出文件表示问题的解答。注意,当N > 26 时,输入文件就不能表示Z 列以后的路障了。(这句话不用专门理他。其实就是从A 的ascii 码开始向后顺延,不管是什么字母就行了。)
输出格式:
输出文件应该只由一行组成,即萨丽能够经过的最多格子数。
思路:
显然是有约束条件的dfs啊,还那么水(其实不用搜索,是个像模拟的东西)
我们从起点开始
由于一开始并没有规定起点,所以在起点我们可以向下方和右方走
题目告诉你,只有碰了壁才能转弯
那很好办,如果前方是墙壁,我就向当前方向的左边和右边搜索
如果前方是已经走过的路,那就说明你已无路可走,直接max取最大即可
如果前方既不是墙,也没走过,那按照题意,你必须走这一格,直接更新即可
最后答案就是更新出来的最大值
代码:
#include<iostream> #include<cstdio> #define rii register int i #define rij register int j using namespace std; int bj[135][135],n,m,zb,ans,pd; char wz; void dfs(int x,int y,int zg,int fx) { if(x==1&&y==1) { if(bj[x+1][y]!=2) { bj[x+1][y]=1; dfs(x+1,y,zg+1,11); bj[x+1][y]=0; } if(bj[x][y+1]!=2) { bj[x][y+1]=1; dfs(x,y+1,zg+1,1); bj[x][y+1]=0; } } if(fx==2) { if(bj[x][y-1]==0) { bj[x][y-1]=1; dfs(x,y-1,zg+1,fx); bj[x][y-1]=0; } if(bj[x][y-1]==2) { if(bj[x+1][y]!=1&&bj[x+1][y]!=2) { bj[x+1][y]=1; dfs(x+1,y,zg+1,11); bj[x+1][y]=0; } if(bj[x-1][y]!=1&&bj[x-1][y]!=2) { bj[x-1][y]=1; dfs(x-1,y,zg+1,12); bj[x-1][y]=0; } } } if(fx==1) { if(bj[x][y+1]==0) { bj[x][y+1]=1; dfs(x,y+1,zg+1,fx); bj[x][y+1]=0; } if(bj[x][y+1]==2) { if(bj[x+1][y]!=1&&bj[x+1][y]!=2) { bj[x+1][y]=1; dfs(x+1,y,zg+1,11); bj[x+1][y]=0; } if(bj[x-1][y]!=1&&bj[x-1][y]!=2) { bj[x-1][y]=1; dfs(x-1,y,zg+1,12); bj[x-1][y]=0; } } } if(fx==11) { if(bj[x+1][y]==0) { bj[x+1][y]=1; dfs(x+1,y,zg+1,fx); bj[x+1][y]=0; } if(bj[x+1][y]==2) { if(bj[x][y+1]!=2&&bj[x][y+1]!=1) { bj[x][y+1]=1; dfs(x,y+1,zg+1,1); bj[x][y+1]=0; } if(bj[x][y-1]!=2&&bj[x][y-1]!=1) { bj[x][y-1]=1; dfs(x,y-1,zg+1,2); bj[x][y-1]=0; } } } if(fx==12) { if(bj[x-1][y]==0) { bj[x-1][y]=1; dfs(x-1,y,zg+1,fx); bj[x-1][y]=0; } if(bj[x-1][y]==2) { if(bj[x][y+1]!=2&&bj[x][y+1]!=1) { bj[x][y+1]=1; dfs(x,y+1,zg+1,1); bj[x][y+1]=0; } if(bj[x][y-1]!=2&&bj[x][y-1]!=1) { bj[x][y-1]=1; dfs(x,y-1,zg+1,2); bj[x][y-1]=0; } } } ans=max(ans,zg); } int main() { scanf("%d%d ",&n,&m); for(rii=0;i<=n+1;i++) { bj[0][i]=2; } for(rii=0;i<=n+1;i++) { bj[i][0]=2; } for(rii=0;i<=n+1;i++) { bj[n+1][i]=2; } for(rii=0;i<=n+1;i++) { bj[i][n+1]=2; } for(rii=1;i<=m;i++) { scanf("%c%d ",&wz,&zb); bj[zb][wz-'A'+1]=2; } bj[1][1]=1; dfs(1,1,1,0); cout<<ans; }