[题解] [Code+#1]Yazid 的新生舞会

题面

题解

upd : (cnt_i) 代表值为 (i) 的个数

我们可以暴力枚举众数 (k)

把等于 (k) 的赋值成 1 , 不等于 (k) 的赋值成 -1

这样原序列就变成了一段折线

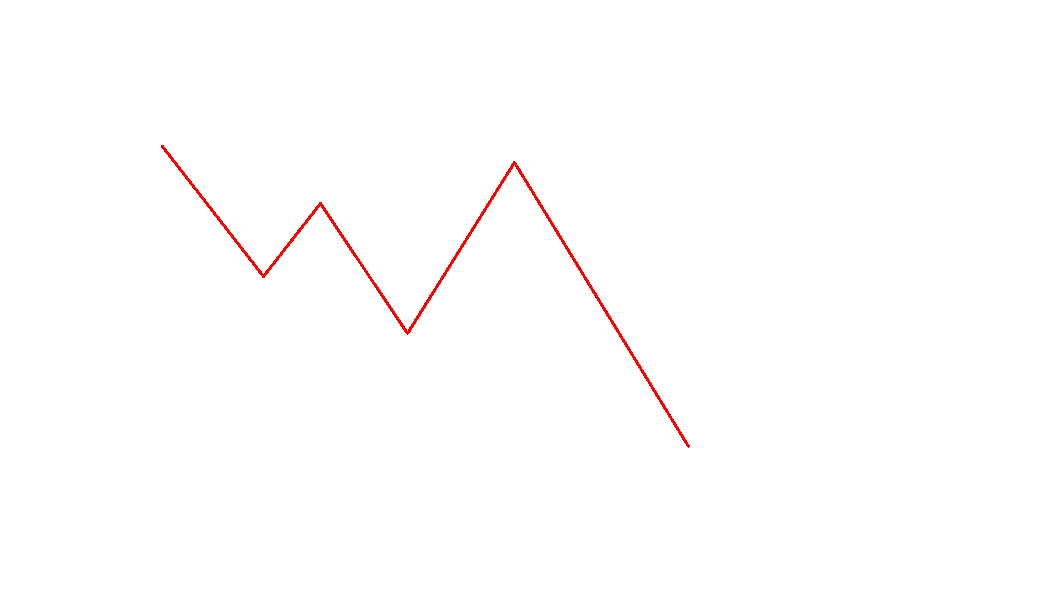
我们把他剖开一段一段来分析

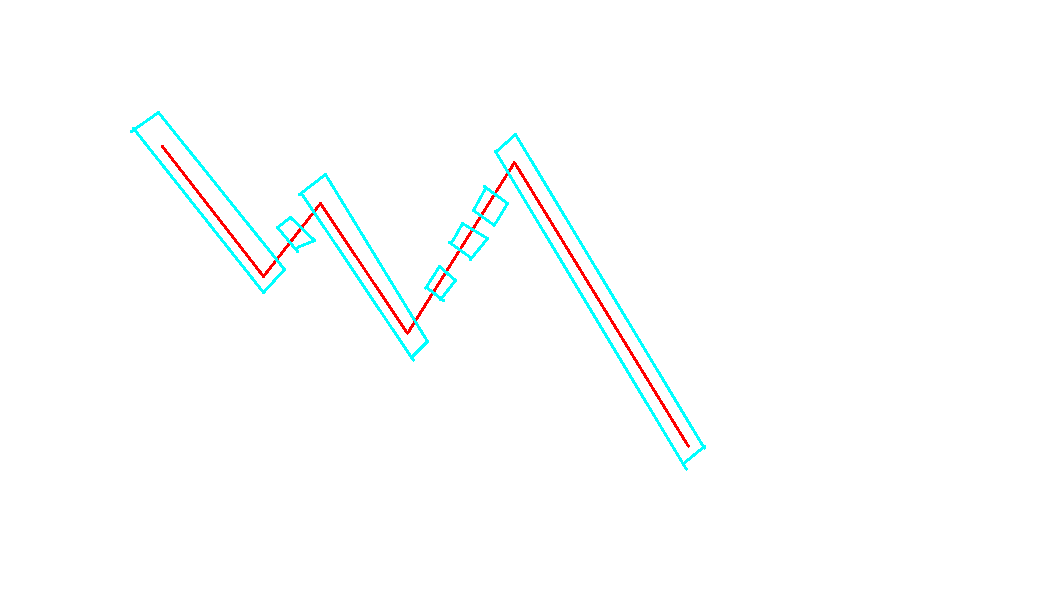
这些蓝线的左右端点分别为, 一个值为众数的数的位置, 和它下一个值为众数的数的位置的前一个位置

为了方便, 我们定义 (0) , (n + 1) 这两个位置上的数可以当做任意一个位置

我们对于一条蓝线扯出来单独分析

设 (sum_i) 为折线在 (i) 这个点的值

只要我们找到两个点满足 (i > j) , 并且满足 (sum_i > sum_j) , 就有序列在 ([j + 1, i]) 上的变化大于 0 , 也就是说是满足区间众数大于区间长度一半的

设它的值域为 ([l, r]) , 暴力做法是这样的

• 对于 (i in [l, r]) , 将 (sum_{j = -infty }^{i - 1} cnt_j) 加入答案贡献

• 把 (cnt_i) 加一

考虑优化这个过程

[displaystyle egin{aligned} ans &= sum_{i = l}^rsum_{j=-infty}^{i - 1}cnt_i\ &= (r - l + 1) sum_{j = -infty}^{l - 1}cnt_i + sum_{i = l}^{r - 1}(r - i)*cnt_i\ &= (r - l + 1) sum_{j = -infty}^{l - 1}cnt_i + r * sum_{i = l} ^ {r - 1}cnt_i - sum_{i = l} ^ {r - 1}i * cnt_i end{aligned} ]

所以我们在线段树上维护 (cnt_i) 和 (i * cnt_i) 即可

然后像上面那样每一个蓝色的线都这么分析

对于一个众数 (k) 它的复杂度为 (O(mlogn)) , (m) 为 (a) 中等于 (k) 的数的个数

所以总的复杂度就是 (O(nlogn))

Code

#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
#include <vector>
typedef long long ll;
const int N = 500005; 
using namespace std;

int n, m, a[N];
struct Tree { ll sum[2], tag; } t[N << 4]; 
vector <int> vec[N]; 
ll ans; 

template < typename T >
inline T read()
{
	T x = 0, w = 1; char c = getchar();
	while(c < '0' || c > '9') { if(c == '-') w = -1; c = getchar(); }
	while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
	return x * w; 
}

void update(int p)
{
	t[p].sum[0] = t[p << 1].sum[0] + t[p << 1 | 1].sum[0]; 
	t[p].sum[1] = t[p << 1].sum[1] + t[p << 1 | 1].sum[1]; 
}

void pushdown(int p, int l, int r)
{
	if(t[p].tag)
	{
		int ls = p << 1, rs = ls | 1, mid = (l + r) >> 1; 
		t[ls].sum[0] += 1ll * t[p].tag * (mid - l + 1), t[ls].tag += t[p].tag; 
		t[ls].sum[1] += 1ll * t[p].tag * (mid + l - m) * (mid - l + 1) / 2; 
		t[rs].sum[0] += 1ll * t[p].tag * (r - mid), t[rs].tag += t[p].tag; 
		t[rs].sum[1] += 1ll * t[p].tag * (mid + r + 1 - m) * (r - mid) / 2; 
		t[p].tag = 0; 
	}
}

void modify(int p, int l, int r, int ql, int qr, int k)
{
	if(l > r || ql > qr) return; 
	if(ql <= l && r <= qr)
	{
		t[p].tag += k; 
		t[p].sum[0] += (r - l + 1) * k; 
		t[p].sum[1] += 1ll * (l + r - m) * (r - l + 1) / 2 * k; 
		return; 
	}
	pushdown(p, l, r);
	int mid = (l + r) >> 1;
	if(ql <= mid) modify(p << 1, l, mid, ql, qr, k);
	if(mid < qr) modify(p << 1 | 1, mid + 1, r, ql, qr, k); 
	update(p); 
}

ll query(int p, int l, int r, int ql, int qr, int op, int opt = 1)
{
	if(l > r || ql > qr) return 0; 
	if(ql <= l && r <= qr)
		return t[p].sum[op]; 
	pushdown(p, l, r);
	int mid = (l + r) >> 1; ll res = 0;
	if(ql <= mid) res = query(p << 1, l, mid, ql, qr, op, opt); 
	if(mid < qr) res = res + query(p << 1 | 1, mid + 1, r, ql, qr, op, opt); 
	update(p); 
	return res; 
}

int main()
{
	n = read <int> (), read <int> ();
	m = n << 1; 
	for(int i = 1; i <= n; i++)
	{
		a[i] = read <int> ();
		vec[a[i]].push_back(i); 
	}
	for(int i = 0; i < n; i++)
		vec[i].push_back(n + 1);
	for(int sz, st, ed, i = 0; i < n; i++)
	{
		sz = vec[i].size();
		if(sz == 1) continue; 
		st = 0; 
		for(int j = 0; j < sz; j++)
		{
			ed = 2 * j + 1 - vec[i][j]; 
			ans += 1ll * (st - ed + 1) * query(1, 1, m, 1, ed - 1 + n, 0)
				       + st * query(1, 1, m, ed + n, st - 1 + n, 0)
				       - query(1, 1, m, ed + n, st - 1 + n, 1); 
			modify(1, 1, m, ed + n, st + n, 1);
			st = ed + 1; 
		}
		st = 0; 
		for(int j = 0; j < sz; j++)
		{
			ed = 2 * j + 1 - vec[i][j]; 
			modify(1, 1, m, ed + n, st + n, -1); 
			st = ed + 1; 
		}
	}
	printf("%lld
", ans); 
	return 0; 
}