（原创）Stanford Machine Learning (by Andrew NG) --- (week 3) Logistic Regression & Regularization

coursera上面Andrew NG的Machine learning课程地址为：https://www.coursera.org/course/ml

我曾经使用Logistic Regression方法进行ctr的预测工作，因为当时主要使用的是成型的工具，对该算法本身并没有什么比较深入的认识，不过可以客观的感受到Logistic Regression的商用价值。

Logistic Regression Model

A. objective function

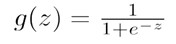      其中z的定义域是(-INF,+INF)，值域是[0,1]

We call this function sigmoid function or logistic function.

We want 0 ≤ h_θ(x) ≤ 1   and  h_θ(x) = g(θ^Tx)  

B. Decision boundary

  在 0 ≤ h_θ(x) ≤ 1的连续空间内，用logistic regression做分类时，我们可以将h_θ(x)等于0.5作为分割点。

•    if  h_θ(x) ≥ 0.5，predict "y = 1";
•    if  h_θ(x) < 0.5，predict "y = 0";

 而Decision Boundary就是能够将所有数据点进行很好地分类的 h(x) 边界。

C. Cost Function

Defination：

 

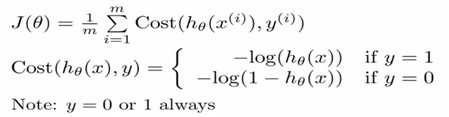
Because y = 0 or y = 1，and cost function can been writen as below:

 

---

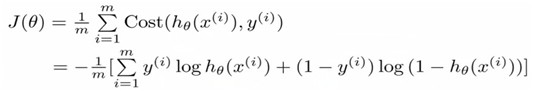
Advanced optimization

In order to minimize J(θ),  and get θ. Then how to get min_θ J(θ) ?

A. Using gradient descent to do optimization

 Repeat{

            }            

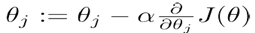
 Compute 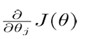, we can get （推导过程下方附录）

 Repeat{

            }

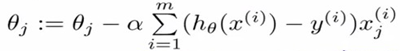
B.其他基于梯度的优化方法

• Conjugate gradient（共轭梯度）
• 牛顿法
• 拟牛顿法
• BFGS（以其发明者Broyden, Fletcher, Goldfarb和Shanno的姓氏首字母命名），公式：
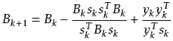
• L-BFGS
• OWLQN

---

Multi classification

How to do multi classification using logistic regression?   （one vs rest）

A. How to train model?

     当训练语料标注的类别大于2时，记为n。我们可以训练n个LR模型，每个模型的训练数据正例是第i类的样本，反例是剩余样本。（1≤ i ≤n）

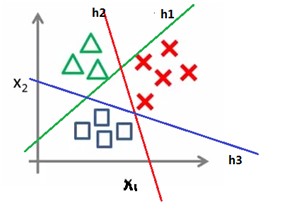
B.How to do prediction? 

    在 n 个 h_θ(x) 中，获得最大 h_θ(x) 的类就是x所分到的类，即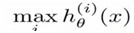 

---

Overfitting

A. How to address overfitting?

     a) Reduce number of features.

• Manually select which features to keep.
• Model selection algorithm (later in course).

      b) Regularization（规范化）

• Keep all the features, but reduce magnitude/values of all parameters .
•  Works well when we have a lot of features, each of which contributes a bit to predicting .

      c) Cross-validation（交叉验证）

• Holdout验证: 我们将语料库分成：训练集，验证集和测试集;
• K-fold cross-validation：优势在于同时重复运用随机产生的子样本进行训练和验证，每次的结果验证一次;

B. Regularized linear regression

   

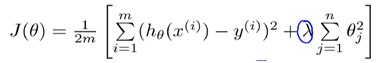
                (式1)

         (式2)

C. Normal equation

    Non-invertibility(optional/advanced).

    suppose m ≤ n                 m: the number of examples;    n: the number of features;

                θ = (X^TX)^-1X^Ty

由(式1)和(式2)可以得到对应的n+1维参数矩阵。

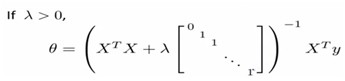
D. Regularized logistic regression

    Regularized cost function：

     J(θ) =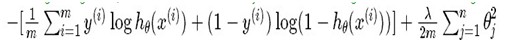   

   Gradient descent: 

      Repeat{

                

              } 

---

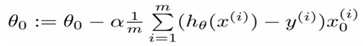
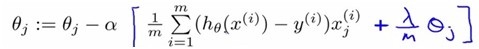
Logistic Regression与Linear Regression的关系

   Logistic Regression是线性回归的一种，Logistic Regression 就是一个被logistic方程归一化后的线性回归。

---

Logistic Regression的适用性

• 可用于概率预测，也可用于分类；
• 仅能用于线性问题；
• 各feature之间不需要满足条件独立假设，但各个feature的贡献是独立计算的。

---

 HOMEWORK

好了，既然看完了视频课程，就来做一下作业吧，下面是Logistic Regression部分作业的核心代码：

1.sigmoid.m

m = 0;
n=0;
[m,n] = size(z);
for i = 1:m
   for j = 1:n
      g(i,j) = 1/(1+e^(-z(i,j)));
   end
end

2.costFunction.m

for i =1:m
   J = J+(-y(i)*log(sigmoid(X(i,:)*theta)))-(1-y(i))*log(1-sigmoid(X(i,:)*theta));
end
J=J/m;
for j=1:size(theta)
   for i=1:m
      grad(j)=grad(j)+(sigmoid(X(i,:)*theta)-y(i))*X(i,j);
   end
grad(j)=grad(j)/m;
end

3.predict.m

for i=1:m
   if(sigmoid(theta'*X(i,:)')>0.5)
      p(i)=1;
   else
      p(i)=0;
   endif
end

4.costFunctionReg.m

for i =1:m
   J = J+(-y(i)*log(sigmoid(X(i,:)*theta)))-(1-y(i))*log(1-sigmoid(X(i,:)*theta));
end
J=J/m;
for j=2:size(theta)
    J = J+(lambda*(theta(j)^2)/(2*m));
end

for j=1:size(theta)
   for i=1:m
      grad(j)=grad(j)+(sigmoid(X(i,:)*theta)-y(i))*X(i,j);
   end
grad(j)=grad(j)/m;
end
for j=2:size(theta)
   grad(j)=grad(j)+(lambda*theta(j))/m;
end

---

 附录

Logistic regression gradient descent 推导过程