谈一下上一篇没说完的几种排序算法,快排,基数排序,与桶排序。
快速排序
1.思路
还是基于分治的思想,这样思考一个有序序列,一个有序序列应该满足任意一个元素(除了边界上的)必然左边的所有元素比自己>=(或者<=),另一边的所有元素比自己<=(或者>=),假如这个性质对于任意一个元素都成立,那么这一定是一个有序序列。快排就是基于这一性质,不断选取元素,使序列满足这一性质,从而分出两个子列,再在子列中选取元素使得子列满足性质,不断递归,最后使序列变成有序序列。
2.伪码
代码应当从原来的序列开始,递归进行以下过程。
- 选取中间元素(一般书籍上称其为枢轴pivot),调整序列满足性质。
- 调整中间元素的左边序列满足性质
- 调整中间元素的右边序列满足性质。
PARTITION(A,p,r) x = A[r] //或者随机选取,并将选取的元素与最后一个元素调换 i = p -1 for j = p to r if A[j] < x i++ exchange A[i],A[j] i = i +1 exchange A[r],A[i] return i QUIKESORT(A,p,r) if p < r q = PARTITION(A,p,r) QUIKESORT(A,p,q-1) QUIKESORT(A,q+1,r)
对于上面代码的正确性我们是可以证明的,对于PARTITION的证明可以如下考虑,循环不变量为数组中p到i为比x小的,i+1到j为比x大的,我们只要证明在循环前循环中循环结束时候上述不变量一直成立,那么就可以利用循环后的不变量得到PARTTION的正确性质,并且不难证明,PARTITION的复杂度是 O(n)的,之后不断在子列上递归,从而使得整个序列满足性质。
3. 复杂度
时间复杂度
我们简单分析一下,快排的时间复杂度是与PARTITION函数密切联系的,划分是否平衡对时间复杂度影响很大,我们如何可以这样理解这种影响,每次调用PARTITION会分出两个子列,我们可以将这种操作表示成一个二叉树的形式。
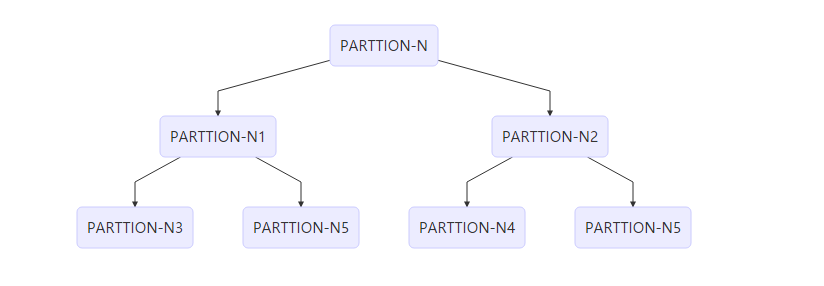
每一层的PARTITION几乎为 O(n)的,感性上可以理解复杂度为每一层的复杂度*层数,当然这是不严谨的,因为有的分支会提前结束,但这不阻碍我们从此理解每次PARTTION对于复杂度的影响。(或者从数学递推的角度T(n)=T(n1)+T(n-n1)+O(n)
最好情况:每次划分出来的左右平衡O(nlog(n)),从上面二叉树的角度分析十分显然。
平均: O(nlogn)
关于这个就比较复杂了,书中的给出的解答是随机选择比较元素的情况,求解算法过程中比较次数的期望,证明了一个O(nlog(n))O(nlog(n))的上界(注意是比较次数的上界,越大代表越复杂),又因为最好情况达到了这个上界,那么期望比较次数必然大于最好情况而小于这个上界,从而得证,相当巧妙精彩(貌似几乎所有经典证明都可以如此描述)。
最差:恰好逆序,O(n2),比较次数为N+(N-1)+····1
当然人们还是为了优化这个时间复杂度不断努力着,上面的随机选取比较元素是一种方法,类似的还有随机选择三个数值,选取中间数作为比较元素。
空间复杂度
原址排序,几乎每层递归不需要开辟新空间,那么主要就是栈空间了上面提到的递归二叉树高度的最大值,不难想到最差情况是O(n)O(n)的,最好情况是恰好平均划分为O(log(n)),那么平均情况呢,大家似乎都认为是log(n),但是大家又说不出个所以然来,我在此给出一个说明,仅仅对于选择随机元素进行划分的情况,我们仍然利用上文中二叉树来表示算法进行的过程,每个节点元素表示为随机选择的元素,那么最后这个的树高期望应该是与以序列元素进行随机构建搜索二叉树的树高期望是一样的,而后者《算法导论》中给出了证明,第三版见P300,是不是很有才,滑稽脸。
当然我们是有办法控制栈深度的,课后习题中先是给我们提到了一种叫做尾递归的技术,
TAIL-RECURSIVE-QUICKSORT(A,p,r) while p < r q = PARTITION(A,p,r) TAIL-RECURSIVE-QUICKSORT(A,p,q-1) p = q + 1
也就是第二个递归并不是必要的,但是仅仅这样是并不能达到我们控制我们栈深度的最差情况的,我们继续进行这样的改进,我们每次PARTTION,后优先递归较短的子列,这样就能使得最差也能让栈深度保持在O(log(n)),代码如下
QSORT(A,p,r) while p < r q = PARTITION(A,p,r) if((q-p) < (r-q)) QSORT(A,p,q-1) p = q + 1 else QSORT(A,q+1,r) r = q -1
稳定性
不稳定,原因是选择的元素与i+1互换导致的,比如 1 2 3(0) 5 6 3(1),选取3(1)为比较元素,那么就会变为1 2 3(1) 5 6 3(0)
小结
读这一部分还是很给我们启发的,比如如何控制栈深度,如何划分的更加平衡,其实还有一个相当有意思的思想是PATTITION中维持循环不变量的方法,虽然我不知道这叫什么思想,但是课后思考题7-6区间模糊排序就可以运用这种思想,题目大概意思是,对于区间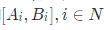
,这样定义区间的次序(不妨设是从大到小),如果排在前面的区间中存在存在元素能比后面区间中的元素大,那么序列就是有序的,比如[1,2],[3,4][5,6],[5,5.5],也就是说,假如两个区间有重叠,那么在次序上谁在前面都是可以的。 下面给出c++代码:
#include<iostream> #include<algorithm> #include<vector> struct Interval { float L; float R; }; int partition(std::vector<Interval> &V, int l, int r) { Interval x = V[r]; int i = l - 1; int k = r ; for (int j = l; j < r; ++j) { if (V[j].R < x.L) { i = i + 1; std::swap(V[i], V[j]); } else if (V[j].L > x.R) { k = k - 1; std::swap(V[k], V[j]); } } std::swap(V[r], V[i + 1]); return (i + 1); } void Intervalsort(std::vector<Interval> &V, int L, int R) { if (L < R) { int q = partition(V, L, R); Intervalsort(V, L, q - 1); Intervalsort(V, q + 1, R); } } void printvector(std::vector<Interval> V) { std::vector<Interval>::iterator it = V.begin(); std::vector<Interval>::iterator end = V.end(); for (; it != end; it++) { std::cout << "[" << (*it).L << "," << (*it).R << "]" << " " << std::endl; } } int main(int argc, char const *argv[]) { std::vector<Interval> V; Interval q1 = { 1,3 }; Interval q2 = { 2,4 }; Interval q8 = { 10,11 }; Interval q9 = { 100,1010 }; Interval q3 = { 6,9 }; Interval q10 = { -1,0 }; Interval q4 = { 4.5,5 }; V.push_back(q1); V.push_back(q2); V.push_back(q3); V.push_back(q4); V.push_back(q8); V.push_back(q9); V.push_back(q10); Intervalsort(V, 0, V.size() - 1); printvector(V); return 0; }
结果输出:

对于前面提到的多线程优化,就比较奇怪,我找了网上好几个版本,都没有stl库里面的sort来的快,由于现在对于c++11的多线程库并不是十分的了解,自己实现还有点困难,准备以后熟悉了再尝试下,而且在此说一点std库里面的的sort在(<algorithm>中)与qsort(在stdlib.h中)的区别,sort是qsort的优化版本,而且实测优化效果十分好,当然测试的时候请不要忘记开启编译器优化,否则可能会出现相反的结果。
sort相比于qsort的优化(参考《STL源码剖析》)
- 前面提到的,用来比较的元素为序列前中后三者中的中间值
- 分割方法采用的是Hoare划分,但是这个是否带来优化我并不知道,也没说其优秀的地方。
- 设置阈值,数据量较小的时候采用插入排序。
- 在子序列较小时停止递归,这时候整个序列接近有序,最后对整体来一次插入排序,因为插入排序对于接近有序的序列表现出相当优秀的性能。在算法导论的课后题有要证明其复杂度为
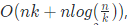 ,其中k为停止递归的阈值,我利用上面提到的二叉树提出一个不太严谨的看法,插入排序时候因为是相对有序的,每次插入k个元素复杂度为O(k^2),共插入k/n次,后者则可以理解为递归的树高从降低了O(logk)。
,其中k为停止递归的阈值,我利用上面提到的二叉树提出一个不太严谨的看法,插入排序时候因为是相对有序的,每次插入k个元素复杂度为O(k^2),共插入k/n次,后者则可以理解为递归的树高从降低了O(logk)。 - 采用introsort,内省式排序,能自动觉察分割导致复杂度朝O(n2)恶化的时候,将排序算法转为堆排序。
比较排序的下界
先是介绍了决策树模型,并将其与比较操作联系在一块推出了一个比较排序的时间复杂度最坏情况的下界为O(nlog(n)),下面我们讨论下可以打破这个界限的非比较排序方法。
计数排序
1.思路
对于一个元素,我们统计比它小的元素的个数,从而知道元素在有序序列中应处的位置,当然对于相同的元素我们要谨慎处理因为不能将他们放在同一个位置。
2.伪码
INSERTION-SORT(A) COUNTING-SORT(A,B,k) //A为输入,B为输出,k为数字范围 for i = 0 to k C[i] = 0 for j = 1 to A.length C[A[j]] = C[A[j]] + 1 for i = 1 to k C[i] = C[i] + 1 for j = A.length dowm to 1 //倒序填充,为的是保证排序的稳定性质 B[C[A[j]]] = A[j] C[A[j]] = C[A[j]] - 1
3. 复杂度
时间复杂度
显然为O(n+k),n为序列元素个数,k为元素大小个数范围,当k为O(n),这个算法效率就相当的可观了。
空间复杂度
为O(n+k),一个计数的数组,一个输出的序列。(当然键值如果相比元素大小可以忽略不计的话,就为(O(n)了。
稳定性
稳定,这相当重要,在基数排序中将会看到
基数排序
举个例子,整形的6位数,那么我们可以先从个位开始对整个序列进行计数排序(或者其他稳定的排序方法),紧接着对十位进行,依次向高位进行,我们专门强调了稳定性,这对算法的正确性起到至关重要的作用。
伪码:
RADIX-SORT(A,d) // A为序列,d为位数 for i = 1 to d use a stable sort to sort Array
时间复杂度
O(d(n+k)) 采用基数排序 注意我们对于位数的划分是灵活的,只要保证后面的位数排序是比先排的优先级是高的,比如你可以先拍十位及以下,然后在此基础上排百位到十万位,对应的时间复杂度是容易分析的,不在赘述,不过我们有着这样的准则,对于位数选的越大,时间复杂度是降低的,最简单直接退化到计数排序,但是相对的空间复杂度也会上升。
空间复杂度
假如是使用的计数排序,那么显然为Od(n+k)
稳定性
显然稳定,
桶排序
算法思想
算法基于这样的假设,输入的数据大体分布是平均的,假设输入数据均匀分布于[0,1],假如大于此区间,就做相应的放缩,将此区间划分为输入数据个桶,将输入元素放到相应的桶的里面,因为数据的均匀性质,基本不会出现许多个元素在一个桶里面的情况,我们先对桶里面的元素进行插入排序,然后按桶次序将桶中元素接起来。
伪码: B为一个放着链表头的数组,A为输入序列
BUCKET-SORT(A) n = A.length for i =0 to n - 1 make B[i] an empty list for i = 1 to n insert A[i] to listB[floor(nA[i])] for i = 0 to n - 1 sort list B[i] with insertsort concatenate the list B[0],B[1]...B[n-1] together in order
时间复杂度
O(n),基于上面的假设,有一点概率论的知识的话还是很容易懂得。
空间复杂度
O(n)
小结
思考为何基数排序与桶排序能获得如此低的时间复杂度,是因为其充分利用了数据的特征,没有忽视这部分信息量。基数是因为我们了解到了数据为一定范围的整数,,桶排序是因为我们了解到了数据的分布,注意,我在此推广下,假如不是均匀分布,我们则可以根据分布调整桶在不同范围的个数,依旧能保证每个桶的元素期望个数为O(1)的,依旧能使算法复杂度为O(n)的。
排序部分到此为止,假如还能有时间就再写写图算法吧,应该不会了,毕竟马上考试了q_q.