手写AVL+图解红黑树

AVL

重点基本上在两个rotate里面

#include<bits/stdc++.h>
using namespace std;
#define N 200005

struct Node{
	int key,height;
	Node* lc;
	Node* rc;
};
Node* root = NULL;

Node* newnode(int key){
	Node* node = new Node();
	node->key=key;
	node->height=1;
	node->lc=node->rc=NULL;
	return node;
}
int h(Node* root){
	if(root==NULL)return 0;
	return root->height;
}

int getBalance(Node* root){
	if(root==NULL)return 0;
	return h(root->lc)-h(root->rc);
}

Node* leftRotate(Node* root){
	Node* t=root->rc;
	root->rc=t->lc;
	t->lc=root;
	root->height=max(h(root->lc),h(root->rc))+1;
	t->height=max(h(t->lc),h(t->rc))+1;
	return t;
}
Node* rightRotate(Node* root){
	Node* t=root->lc;
	root->lc=t->rc;
	t->rc=root;
	root->height=max(h(root->lc),h(root->rc))+1;
	t->height=max(h(t->lc),h(t->rc))+1;
	return t;
}
Node* LRRotate(Node* root){
	root->lc=leftRotate(root->lc);
	return rightRotate(root);
}
Node* RLRotate(Node* root){
	root->rc=rightRotate(root->rc);
	return leftRotate(root);
}

Node* rotate(Node* root){
	int balance=getBalance(root);
	if(balance == 2 && getBalance(root->lc)>=0)//右旋 
		return rightRotate(root);
	if(balance == -2 && getBalance(root->rc)<0)//左旋 
		return leftRotate(root);
	if(balance == 2)//左旋+右旋 
		return LRRotate(root);
	if(balance == -2)//右旋+左旋 
		return RLRotate(root);
	return root;
}

Node* insert(Node* root, int key){
	if(root == NULL)return newnode(key);
	if(key==root->key)return root;
	
	if(key<root->key) root->lc = insert(root->lc,key);
	else if(key>root->key) root->rc = insert(root->rc,key);
	root->height = max(h(root->lc),h(root->rc))+1;
	
	return root=rotate(root); // 调整平衡 
}

Node* minValueNode(Node *root){//找root子树里最小值 
	Node* res=root;
	while(res->lc)res=res->lc;
	return res; 
}

Node* del(Node* root, int key){
	if(root == NULL)return root;
	if(key<root->key)root->lc=del(root->lc,key);
	else if(key>root->key)root->rc=del(root->rc,key);
	else {//删该点 
		if(root->lc==NULL || root->rc==NULL){//缺了一个儿子 
			Node* t=root->lc?root->lc:root->rc;
			if(t==NULL){t=root;root=NULL;}//叶子节点 
			else *root=*t;
			free(t);
		} 
		else {//把右子树最小结点提上来 
			Node* t = minValueNode(root->rc); 
			root->key = t->key;
			root->rc = del(root->rc,t->key);			
		}
	}
	
	if(root==NULL)return root;//root是叶子 
	
	root->height = max(h(root->lc),h(root->rc))+1;
	
	return root=rotate(root);
}

void printPre(Node* root){
	if(root==NULL)return;
	cout<<root->key<<'
';
	printPre(root->lc);
	printPre(root->rc);
}

void printMid(Node* root){
	if(root==NULL)return;
	printMid(root->lc);
	cout<<root->key<<'
';
	printMid(root->rc);
}

int main(){/*
	root = insert(root,10);
	root = insert(root,20);
	root = insert(root,30);
	root = insert(root,40);
	root = insert(root,35);
	*/
	root = insert(root, 9);
    root = insert(root, 5);
    root = insert(root, 10);
    root = insert(root, 0);
    root = insert(root, 6);
    root = insert(root, 11);
    root = insert(root, -1);
    root = insert(root, 1);
    root = insert(root, 2);

	root = del(root,9);
	printMid(root);
	puts("");
	root = del(root,1);
	printMid(root);
}

红黑树

红黑树的其它原理和AVL高度相似，不同之处在于其保持平衡的策略

1.红黑树是一棵平衡二叉搜索树，其中序遍历单调不减。
2.节点是红色或黑色。
3.根节点是黑色。
4.每个叶节点(也有称外部节点的，目的是将红黑树变为真二叉树，即NULL节点，空节点)是黑色的。
5.每个红色节点的两个子节点都是黑色。(换句话说，从每个叶子到根的所有路径上不能有两个连续的红色节点)
6.从根节点到每个叶子的所有路径都包含相同数目的黑色节点（这个数值叫做黑高度）。

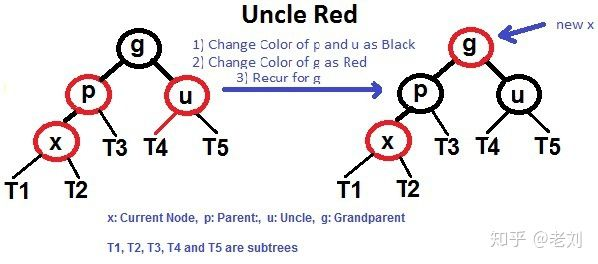
所以，往红黑树里insert结点时的结点必定先设置为红色(保证性质6)。如果出现了双红现象，以下分为两种情况

设插入的点是x

1.不用rotate,只需要重新染色：x的父亲和叔叔都是红色

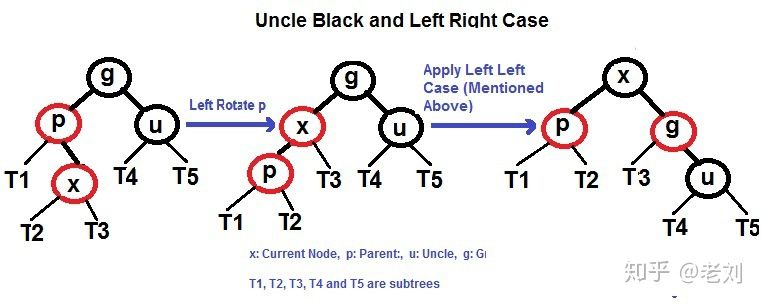
2.需要rotate : x的父亲p是红色，叔叔u是黑色，此时rotate(x的祖父g)，然后将p和g重新染色

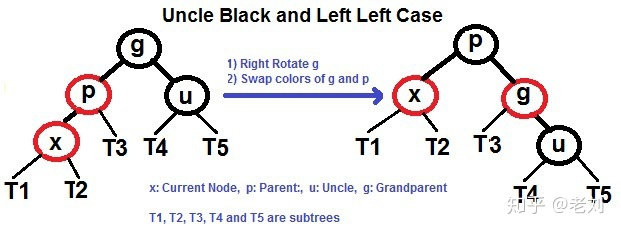
和AVL一样，rotate会有另外一种情况，此时需要rotate两下！