各位dalao的解法都好神啊。。。
这里给一种点分治的解法。
题目
思路
首先斜率部分。
转移方程:
(ans[x]=min(-dis[u]*p[x]+ans[u])+dis[x]*p[x]+q[x])
发现结果只与(min())框内的部分有关,观察这个形式,发现是个一次函数,也就是说可以斜率优化。
dalao们对于推斜率式子这部分表示很不屑,但是我太菜了,所以还是写一下吧。
令(p=p[x]),当(u)的结果比(v)更优且(u)是(v)的儿子时:
[---dis[u]*p+ans[u]<-dis[v]*p+ans[v]\
-->(dis[u]-dis[v])*p>ans[u]-ans[v]\
-->p>(ans[u]-ans[v])/(dis[u]-dis[v])(在此题中如果u是v的父亲,则dis[u]>dis[v],故符号不变)\
]
然后从根到当前点,维护一个斜率单调递增的栈,放张图感受一下:
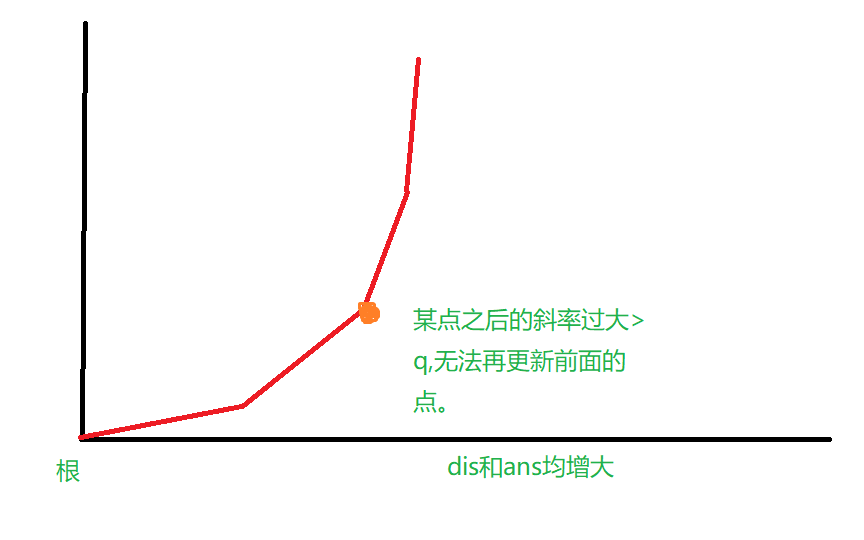
以上算是补充了dalao们省略的部分。
下面就是点分了。
对于某一点而言,我们有一下流程更新它的子树的答案:
- 算出它所有祖先的ans
- 用它的祖先更新它子树中的点
- 用它自己更新子树中的点
在此过程中,维护上述所说的栈,然后二分找到图中橙色标注的这个最优点,更新答案。
至于(l)的限制该怎么处理呢?可以将它的祖先按照(l)排序,利用一种类似归并排序的做法,将这一约束加上去,就可以了。
具体细节见代码吧。
ps:我代码中的顺序与图中相反(由儿子到父亲),不过这并不影响。
代码
#include<bits/stdc++.h>
#define LL long long
#define M 200005
using namespace std;
int n,fa[M],h[M],tot;
LL p[M],q[M],l[M],dis[M],ans[M];
int qq[M],stk[M],top;
struct edge{int nxt,to;}G[M<<1];
void Add(int a,int b){
G[++tot]=(edge){h[a],b};
h[a]=tot;
}
int sz[M],rt,mx[M],tt;
bool vis[M];
void dfsrt(int x,int f){
sz[x]=1;mx[x]=0;
for(int i=h[x];i;i=G[i].nxt){
int u=G[i].to;
if(u==f||vis[u])continue;
dfsrt(u,x);
sz[x]+=sz[u];
mx[x]=max(mx[x],sz[u]);
}
mx[x]=max(mx[x],tt-mx[x]);
if(mx[x]<mx[rt])rt=x;
}
void dfssz(int x,int f){
sz[x]=1;
for(int i=h[x];i;i=G[i].nxt){
int u=G[i].to;
if(u==f||vis[u])continue;
dfssz(u,x);
sz[x]+=sz[u];
}
}
bool cmp(int a,int b){return l[a]>l[b];}
double calcK(int u,int v){return (double)(ans[u]-ans[v])/(dis[u]-dis[v]);}
void dfsqq(int x,int f){
qq[++qq[0]]=x;
for(int i=h[x];i;i=G[i].nxt){
int u=G[i].to;
if(u==f||vis[u])continue;
dfsqq(u,x);
}
}
void solve(int x,int f){//f表示对于当前x来说,fa[x]及以上的祖先的影响已经算过了,不需要重复计算
dfssz(x,-1);//重新计算sz
vis[x]=1;
if(x!=1&&!vis[fa[x]]){//计算一个点之前,它的祖先要先计算出来
tt=sz[fa[x]];rt=0;
dfsrt(fa[x],-1);
solve(rt,f);
}
qq[0]=0;dfsqq(x,fa[x]);
sort(qq+1,qq+qq[0]+1,cmp);
top=0;
for(int i=1,now=fa[x];i<=qq[0];i++){//用当前点的父亲更新当前点的子树
while(now!=fa[f]/*保证不超过这棵子树,保证复杂度*/&&l[qq[i]]<=dis[now]){
while(top>1&&calcK(stk[top-1],stk[top])<=calcK(stk[top],now))top--;
stk[++top]=now;now=fa[now];
}
if(!top)continue;
int l=1,r=top;
while(l!=r){
int mid=(l+r)>>1;
if(calcK(stk[mid],stk[mid+1])<(double)p[qq[i]])r=mid;
else l=mid+1;
}
int j=qq[i];
ans[j]=min(ans[j],ans[stk[l]]+(dis[j]-dis[stk[l]])*p[j]+q[j]);
}
for(int i=1;i<=qq[0];i++){
if(qq[i]!=x&&l[qq[i]]<=dis[x]){
int j=qq[i];
ans[j]=min(ans[j],ans[x]+(dis[j]-dis[x])*p[j]+q[j]);
}
}
for(int i=h[x];i;i=G[i].nxt){
int u=G[i].to;
if(!vis[u]&&u!=fa[x]){
tt=sz[u];rt=0;
dfsrt(u,x);
solve(rt,u);
}
}
}
int t;
int main(){
scanf("%d%d",&n,&t);
mx[0]=1e9;
memset(ans,0x3f,sizeof(ans));
ans[1]=0;
for(int i=2;i<=n;i++){
LL ds;
scanf("%d%lld%lld%lld%lld",&fa[i],&ds,&p[i],&q[i],&l[i]);
Add(i,fa[i]);Add(fa[i],i);
dis[i]=dis[fa[i]]+ds;
}
for(int i=2;i<=n;i++)l[i]=dis[i]-l[i];
tt=n;
dfsrt(1,-1);
solve(rt,1);
for(int i=2;i<=n;i++)printf("%lld
",ans[i]);
return 0;
}