题目描述
Mayan puzzle是最近流行起来的一个游戏。游戏界面是一个 7 行5 列的棋盘,上面堆放着一些方块,方块不能悬空堆放,即方块必须放在最下面一行,或者放在其他方块之上。游戏通关是指在规定的步数内消除所有的方块,消除方块的规则如下:
1 、每步移动可以且仅可以沿横向(即向左或向右)拖动某一方块一格:当拖动这一方块时,如果拖动后到达的位置(以下称目标位置)也有方块,那么这两个方块将交换位置(参见输入输出样例说明中的图6 到图7 );如果目标位置上没有方块,那么被拖动的方块将从原来的竖列中抽出,并从目标位置上掉落(直到不悬空,参见下面图1 和图2);
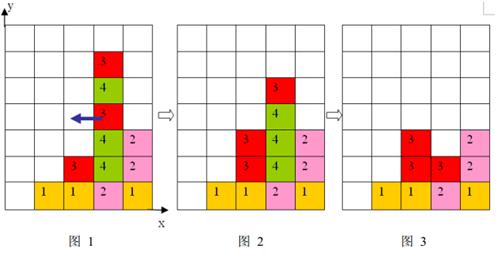
2 、任一时刻,如果在一横行或者竖列上有连续三个或者三个以上相同颜色的方块,则它们将立即被消除(参见图1 到图3)。
注意:
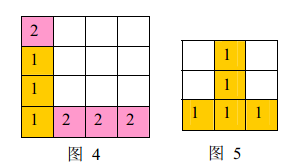
a) 如果同时有多组方块满足消除条件,几组方块会同时被消除(例如下面图4 ,三个颜色为1 的方块和三个颜色为 2 的方块会同时被消除,最后剩下一个颜色为 2 的方块)。
b) 当出现行和列都满足消除条件且行列共享某个方块时,行和列上满足消除条件的所有方块会被同时消除(例如下面图5 所示的情形,5 个方块会同时被消除)。
3 、方块消除之后,消除位置之上的方块将掉落,掉落后可能会引起新的方块消除。注意:掉落的过程中将不会有方块的消除。
上面图1 到图 3 给出了在棋盘上移动一块方块之后棋盘的变化。棋盘的左下角方块的坐标为(0, 0 ),将位于(3, 3 )的方块向左移动之后,游戏界面从图 1 变成图 2 所示的状态,此时在一竖列上有连续三块颜色为4 的方块,满足消除条件,消除连续3 块颜色为4 的方块后,上方的颜色为3 的方块掉落,形成图 3 所示的局面。
输入输出格式
输入格式:
输入文件mayan.in,共 6 行。
第一行为一个正整数n ,表示要求游戏通关的步数。
接下来的5 行,描述 7*5 的游戏界面。每行若干个整数,每两个整数之间用一个空格隔开,每行以一个0 结束,自下向上表示每竖列方块的颜色编号(颜色不多于10种,从1 开始顺序编号,相同数字表示相同颜色)。
输入数据保证初始棋盘中没有可以消除的方块。
输出格式:
输出文件名为mayan.out。
如果有解决方案,输出 n 行,每行包含 3 个整数x,y,g ,表示一次移动,每两个整数之间用一个空格隔开,其中(x ,y)表示要移动的方块的坐标,g 表示移动的方向,1 表示向右移动,-1表示向左移动。注意:多组解时,按照 x 为第一关健字,y 为第二关健字,1优先于-1 ,给出一组字典序最小的解。游戏界面左下角的坐标为(0 ,0 )。
如果没有解决方案,输出一行,包含一个整数-1。
输入输出样例
3 1 0 2 1 0 2 3 4 0 3 1 0 2 4 3 4 0
2 1 1 3 1 1 3 0 1
说明
【输入输出样例说明】
按箭头方向的顺序分别为图6 到图11
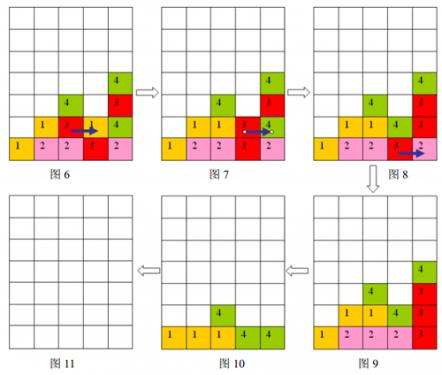
样例输入的游戏局面如上面第一个图片所示,依次移动的三步是:(2 ,1 )处的方格向右移动,(3,1 )处的方格向右移动,(3 ,0)处的方格向右移动,最后可以将棋盘上所有方块消除。
【数据范围】
对于30% 的数据,初始棋盘上的方块都在棋盘的最下面一行;
对于100%的数据,0 < n≤5 。
时限3s。
noip2011提高组day1第3题
- NOIP2011 day1t3,一道比较恶心的搜索题。
- 该题目是关于一个叫做玛雅游戏的东西。
- 根据题意可以看出应该用搜索(并且是深度优先搜索,因为本题深度较小)。
- 至于实现起来比较难的部分是掉落和清除,写丑了很难受的(第一次写时候写了200多行)。
- 清除可以用打标记来实现,记住要先掉落在清除,每次清除后判断是否能继续掉落。
- 本题需要一些剪枝策略,否则后4个点会tle。
- 比较重要的剪枝:优先搜左边换右边(或者右边换左边的0),因为要保证x的字典序最小的方案,所以优先选择左边换右边来代替右边换左边。
- 弱一点的剪枝:当图中有某种颜色的格子为1个或2个是时退出搜索,因为该方案不成立。
- 时限3s,所以写的不是很丑就能过啦
附上代码
1 var 2 q,n,m,i,j,x :longint; 3 map :array[-5..10,-5..10,0..10] of longint; 4 ansx,ansy,ansf :array[0..10] of longint; 5 cur :array[-5..10,-5..10] of longint; 6 f :array[-5..10,-5..10] of boolean; 7 fff :boolean; 8 col :array[0..20] of longint; 9 10 procedure swap(var x,y:longint); 11 var 12 z :longint; 13 begin 14 z:=x; 15 x:=y; 16 y:=z; 17 end; 18 19 function clear:boolean; 20 var 21 i,j,k,l :longint; 22 ff :boolean; 23 begin 24 fillchar(f,sizeof(f),false); 25 ff:=false; 26 for i:=0 to n-1 do 27 for j:=0 to m-1 do 28 begin 29 if cur[i,j]=0 then continue; 30 if (cur[i,j]=cur[i-1,j]) and (cur[i,j]=cur[i-2,j]) then 31 begin 32 f[i,j]:=true; 33 f[i-1,j]:=true; 34 f[i-2,j]:=true; 35 end; 36 if (cur[i,j]=cur[i,j-1]) and (cur[i,j-1]=cur[i,j-2]) then 37 begin 38 f[i,j]:=true; 39 f[i,j-1]:=true; 40 f[i,j-2]:=true; 41 end; 42 end; 43 for i:=0 to n-1 do 44 for j:=0 to m-1 do if f[i,j] then 45 begin 46 ff:=true; 47 cur[i,j]:=0; 48 end; 49 exit(ff); 50 end; 51 52 procedure fall; 53 var 54 k,t,i,j :longint; 55 begin 56 for i:=0 to n-1 do 57 begin 58 k:=0; 59 for j:=0 to m-1 do 60 begin 61 t:=cur[i,j]; 62 cur[i,j]:=0; 63 if (t<>0) then 64 begin 65 cur[i,k]:=t; 66 inc(k); 67 end; 68 end; 69 end; 70 end; 71 72 procedure make(x,y,r,k:longint); 73 var 74 i,j,sum :longint; 75 begin 76 for i:=0 to n-1 do 77 for j:=0 to m-1 do cur[i,j]:=map[i,j,r]; 78 if (k=1) then swap(cur[x,y],cur[x-1,y]) else swap(cur[x,y],cur[x+1,y]); 79 repeat fall until (not clear); 80 fall; 81 sum:=0; 82 for i:=0 to n-1 do 83 for j:=0 to m-1 do map[i,j,r+1]:=cur[i,j]; 84 end; 85 86 function check(x:longint):boolean; 87 var 88 i,j :longint; 89 begin 90 for i:=0 to n-1 do 91 for j:=0 to m-1 do if (map[i,j,x]<>0) then exit(false); 92 exit(true); 93 end; 94 95 function check2(x:longint):boolean; 96 var 97 i,j :longint; 98 begin 99 fillchar(col,sizeof(col),0); 100 for i:=0 to n-1 do 101 for j:=0 to m-1 do if (map[i,j,x]<>0) then inc(col[map[i,j,x]]); 102 for i:=1 to 10 do 103 begin 104 if (col[i]>0) and (col[i]<3) then exit(true); 105 end; 106 exit(false); 107 end; 108 109 procedure dfs(x:longint); 110 var 111 i,j,k :longint; 112 begin 113 if x>q then 114 begin 115 if check(x-1) then 116 begin 117 for i:=1 to q do if ansf[i]=1 then ansf[i]:=-1 else ansf[i]:=1; 118 for i:=1 to q do writeln(ansx[i],' ',ansy[i],' ',ansf[i]); 119 halt; 120 end else exit; 121 end; 122 if check2(x-1) then exit; 123 for i:=0 to n-1 do 124 begin 125 for j:=0 to m-1 do 126 begin 127 if map[i,j,x-1]=0 then continue; 128 if (i>0) and (map[i-1,j,x-1]=0) then 129 begin 130 fff:=true; 131 ansx[x]:=i; 132 ansy[x]:=j; 133 ansf[x]:=1; 134 make(i,j,x-1,1); 135 if fff then dfs(x+1); 136 end; 137 if (i<n-1) then 138 begin 139 fff:=true; 140 ansx[x]:=i; 141 ansy[x]:=j; 142 ansf[x]:=2; 143 make(i,j,x-1,2); 144 if fff then dfs(x+1); 145 end; 146 end; 147 end; 148 end; 149 150 begin 151 read(q); 152 n:=5; 153 m:=7; 154 for i:=0 to n-1 do 155 begin 156 j:=-1; 157 while true do 158 begin 159 read(x); 160 if x=0 then break; 161 inc(j); 162 map[i,j,0]:=x; 163 end; 164 end; 165 dfs(1); 166 writeln(-1); 167 close(input); 168 close(output); 169 end.