宅男计划

题解

$dp$不行考虑三分

发现单峰

1.理性打表,得到单峰

2.感性思考,你会发现你买食物次数越多,你钱数越少,你买的好食品更多,你买食物次数越少,你钱数越多,然而你必须买一些价格贵保质期长弥补次数少.

单峰,我们三分就完了(其实也可以模拟退火,然而我参数爆炸了一直60分)

那么$check$怎么写?

贪心,

考虑排序

考虑先以保质期排序,然后再以价格排序去掉垃圾(在保质期相同不需要买更贵的,那么它就是垃圾完全没必要买它)

考虑以价格排序,在保质期相同时买保质期长的

用保质期排序那么先买保质期长的,还是保质期短的难以确定,所以尝试以价格为基础排序

我的贪心先贪每一次送外卖都买的,再贪不能全买的,两个相加

ll check(ll x){
    ll left=m-x*f;//计算还剩多少钱
    ll w=left/x;//计算每一轮吃了多少
    ll left2=left-w*x;//计算当无法再每一伦都吃情况下剩多少钱
    ll now=0,ans=0,j;//now每一轮活的天数,ans计算剩余不能每一轮都吃能活多少天
    if(left<0) return 0;//若所有钱全用来买外卖了return 0 
    for(ll i=1;i<=n;i++){
        ll fen;
        if(a[i].t>=now&&(w-a[i].val>=0)){
            fen=min(a[i].t-now+1,w/a[i].val);//能买多少,注意和(a[i].t-now+1)
            w-=fen*a[i].val;//剩下钱数减少
            now+=fen;//每一轮活了now天
        }
        j=i;
        if(w-a[i].val<0) break;
    }
    left2+=w*x;//剩下钱累加在left2上
    ll p;
//和上文类似
    for(ll i=j;i<=n;i++) {
        if((a[i].t>=now)&&(left2-a[i].val>=0)) {
            p=min(left2/a[i].val,x);
               ans+=p;
            left2-=p*a[i].t;
            }
            if(ans>0)break;
        }

    return ans+now*x;
}

 总代码我就不放了,我的AC代码有些问题,等改了再放

扯淡

一开始以为是dp,然后愉快的推式子,一看范围

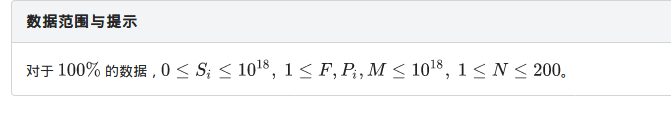
好像$dp$不行,我推的dp以M为基础,总觉得$dp$很玄学

最裸的$dp$  :$f[i][j]$表示运了$i$趟食物,剩余钱$j$

$f[i][j]=f[i-1][j-?]+?$总算写出来,然而样例过不了.假设你每买一个你就多活一天

$f[i][j]$表示不了过期然后

$f[i][j][k]$表示$i趟j容积k保质期$这样可以推了

$f[i][j][k]=f[i][j-w][k-1]$   $f[i+1][j][0]=f[i][j-w][last]$

本来就时空双爆

考虑二分答案?,不是单调的,模拟退火?

于是我开始愉快的退火了,

然而$check$又非常难写,总算过了样例然而交上去

 我以为我调参不行然而我改了也还是$10$分发现$check$写错了,交一发$10$

改成三分$30$分

奇妙的是改了改三分变成了$50$,我认为我三分板子错了,去看三分板子,然而并不是三分错了

觉得$check$太恶心了換了种写法在洛谷上交突然$70$分,然后我忘了我改了哪里突然就又变成了$90$分,那时是$19:27$我觉得胜利在望

然后改了很多地方仍然$90$,觉得很玄学,开始觉得自己爆$long long$事实上它确实爆了$long long$,我$check$写法太$丑$三个*连在一起爆炸了

然后又改回原来$check$一直$50$  $50$  $50$  $50$,最后还是写法丑挂掉了

我的比较函数挂掉了

我不知道应该买先过期,还是保质期长的,然而我又以时间排序,然后他就挂了

改成买便宜的,$AC$了

事实上以时间排序可以$AC$

去掉垃圾食品就完了,我又图省事没去掉垃圾,

你先以时间排序,再以价值排序也可以然而我没采取任何一种方案

然后我就一直挂一直挂