description
solution:
维护每个点的绝对高度十分困难,于是我们只考虑相对高度
我们利用线段树维护一段区间(注意区间是轨道的区间而不是点的区间)
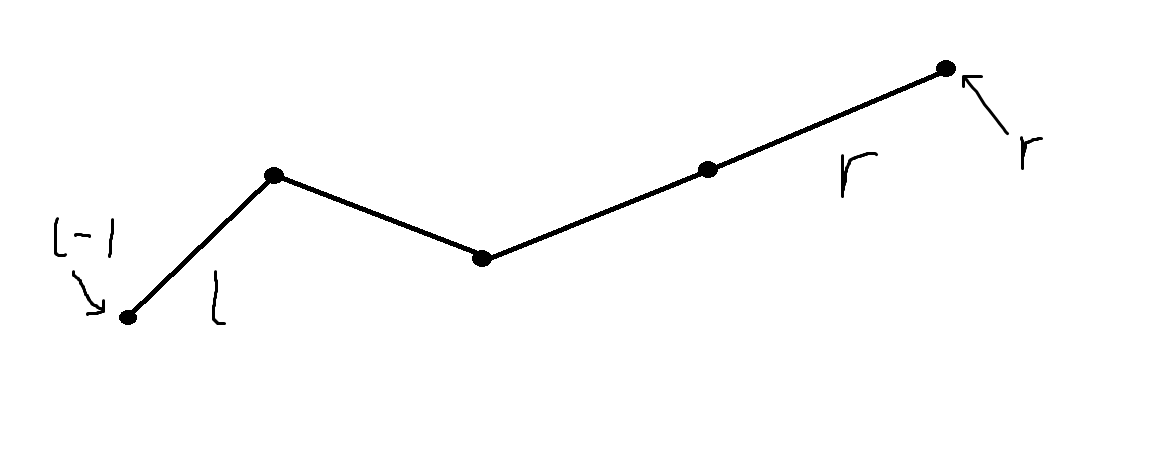
每段区间都要维护三个值:标记,右端点和左端点相对高度以及当前线段中最高点和左端点的相对高度
询问的时候就在线段树上二分就行了
然后就十分好做了
code:
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5,inf=0x3f3f3f3f;
struct SGT
{
int lc[N<<6],rc[N<<6],mx[N<<6],sm[N<<6],tag[N<<6],tot;//note that the space is enough
inline void nd(int&rt)
{
if(rt)return;
rt=++tot;lc[rt]=rc[rt]=0;
tag[rt]=-inf;mx[rt]=sm[rt]=0;
}
inline void mt(int&rt,int l,int r,int v)
{
nd(rt);sm[rt]=(r-l+1)*v;
mx[rt]=max(0,sm[rt]),tag[rt]=v;
}
inline void up(int rt)
{
sm[rt]=sm[lc[rt]]+sm[rc[rt]];
mx[rt]=max(mx[lc[rt]],sm[lc[rt]]+mx[rc[rt]]);
}
inline void down(int rt,int l,int r)
{
if(tag[rt]==-inf)return;
int mid=l+r>>1,&tg=tag[rt];
mt(lc[rt],l,mid,tg),mt(rc[rt],mid+1,r,tg);
tg=-inf;
}
void update(int&rt,int l,int r,int ul,int ur,int v)
{
nd(rt);
if(ul<=l&&r<=ur)return mt(rt,l,r,v);
down(rt,l,r);int mid=l+r>>1;
if(ul<=mid)update(lc[rt],l,mid,ul,ur,v);
if(mid<ur)update(rc[rt],mid+1,r,ul,ur,v);
up(rt);
}
int query(int rt,int l,int r,int v)
{
if(l==r)return v>=sm[rt]?l:l-1;
down(rt,l,r);int mid=l+r>>1;
if(mx[lc[rt]]<=v)return query(rc[rt],mid+1,r,v-sm[lc[rt]]);
else return query(lc[rt],l,mid,v);
}
}T;
int n,RT;
char opt[5];
int main()
{
scanf("%d",&n);T.update(RT,1,n,1,n,0);
while(1)
{
scanf("%s",opt);
if(opt[0]=='E')break;
if(opt[0]=='I')
{
int l,r,v;scanf("%d%d%d",&l,&r,&v);
T.update(RT,1,n,l,r,v);
}
else
{
int v;scanf("%d",&v);
printf("%d
",T.query(RT,1,n,v));
}
}
return 0;
}