Headmaster's Headache UVA - 10817
description:
有S个课程,M个在职教师和N个求职者,每个人都需要被付一定的工资教某些特定的课程(这些信息均会被输入)。现在求最小的工资之和使得每门课都至少有两个教师教
p.s.在职教师不能辞退
data range:
(Sle 8)
(Mle 20)
(Nle 100)
solution:
很明显这是一道状压dp,思路也算比较巧妙吧
初始想法是用三进制进行状压,但是这样十分难做
后来发现因为课程数极小,
因此考虑用(dp_{i,s1,s2})表示从第i个人考虑到最后一个人恰能被一名教师教的集合为s1,被至少两名教师教的集合为s2时的最小支出
(均不在两个集合中意味着没有任何一名教师教)
那么就根据当前的决策(选或不选)进行转移
至于在职教师,我们硬点他们必须被选就可以了
#include<bits/stdc++.h>
using namespace std;
const int N=125,S=8,inf=1e9;
int s,m,n,c[N],st[N],f[N][1<<S][1<<S];
int dp(int pos,int s0,int s1,int s2)
{
if(pos==n+m+1)return (s2==(1<<s)-1?0:inf);
int &d=f[pos][s1][s2];
if(d>=0)return d;
d=inf;
if(pos>m)d=dp(pos+1,s0,s1,s2);
int m0=st[pos]&s0,m1=st[pos]&s1;
s0^=m0,s1=(s1^m1)|m0,s2|=m1;
d=min(d,c[pos]+dp(pos+1,s0,s1,s2));
return d;
}
int main()
{
while(scanf("%d%d%d",&s,&m,&n)==3&&s)
{
for(int i=1;i<=n+m;++i)
{
scanf("%d",c+i);
string s;getline(cin,s);
stringstream ss(s);int num;st[i]=0;
while(ss>>num)st[i]|=(1<<(num-1));
}
memset(f,-1,sizeof(f));
printf("%d
",dp(1,(1<<s)-1,0,0));
}
return 0;
}
description:
有n个物品,每个物品都有m个特征中的某些特征(用01串表示:0表示没有而1表示有)
现在某人心中想到一个物品w,每次你可以询问w是否拥有某一个特征。
求在最坏的情况下你最少询问多少次才能确定这个物品
data range:
(Nle 128)
(Mle 11)
solution:
这道题思路十分巧妙啊
我们记(dp_{s,a})表示已经问了的特征为集合s,其中w拥有的特征集合为a时的答案
转移时考虑枚举每一个我们还没有问过的特征,设其为第i个
那么就有如下的状态转移方程:
(dp_{s,a}=min_i(max(dp_{s|(1<<i),a},dp_{s|(1<<i),a|(1<<i))})+1))
边界条件就是询问集合为s时满足a中特征且s-a中的特征均不满足的只有唯一一个物品的时候,返回0即可
因此我们还要维护一个(cnt_{s,a})数组处理上述的东西
至于如何维护,直接枚举所有集合和物品就可以了
#include<bits/stdc++.h>
using namespace std;
const int M=11,N=130,inf=1e9;
int m,n,cnt[1<<M][1<<M],f[1<<M][1<<M];
int dp(int s,int a)
{
if(cnt[s][a]==1)return 0;
int &d=f[s][a];
if(d>=0)return d;d=inf;
for(int i=0;i<m;++i)
if(!(s&(1<<i)))
{
int ns=s|(1<<i),na=a|(1<<i);
if(cnt[ns][a]<1||cnt[ns][na]<1)continue;
d=min(d,max(dp(ns,a),dp(ns,na))+1);
}
return d;
}
int main()
{
while(scanf("%d%d",&m,&n)==2&&m&&n)
{
char ch[M];int st=(1<<m);
memset(cnt,0,sizeof(cnt));
for(int i=1;i<=n;++i)
{
scanf("%s",ch);int num=0;
for(int j=0;j<m;++j)
if(ch[j]=='1')num|=(1<<j);
for(int k=0;k<st;++k)++cnt[k][k&num];
}
memset(f,-1,sizeof(f));
printf("%d
",dp(0,0));
}
return 0;
}
description:
data range:
solution:
真是一道神题呢!
容易发现对于每一天,每一种股票持有的手数不超过8
于是我们就可以用9进制来状压dp了
记(f_{i,s})表示在从开始到第i天,持有的股票状态为s时能够得到的最大收益
为什么不能定义为从第i天开始到最后一天呢?
那是因为买股票不能赊账,所以必须知道当前的收益,因此就不能
至于状态转移,直接枚举每一支股票,能买就买,能卖就卖地转移
这看起来是一个十分优秀的做法
但是每一次状态转移都会涉及到编码和解码的问题,不仅难写还容易TLE
于是我们可以先预处理所有合法的状态(其实不多)以及买或卖某支股票转移到的状态
采用刷表法,转移的时候记下从哪里转移过来的就可以输出答案了
code:
#include<bits/stdc++.h>
using namespace std;
const int N=10,M=105,NUM=1e5;
typedef double db;
int m,n,totk,s[N],k[N],buy[NUM][N],sell[NUM][N],pre[M][NUM],opt[M][NUM];
db c,f[M][NUM],t[N][M];
char ch[N][10];
map<vector<int>,int>mp;
vector<vector<int> >st;
void predfs(int pos,int cnt,vector<int>&v)
{
if(pos==n)
{
mp[v]=st.size();
st.push_back(v);
return;
}
for(int i=0;i<=k[pos]&&i+cnt<=totk;++i)
{
v.push_back(i);
predfs(pos+1,cnt+i,v);
v.pop_back();
}
}
inline void _init()
{
memset(buy,-1,sizeof(buy));
memset(sell,-1,sizeof(sell));
for(int i=0;i<st.size();++i)
{
int num=0,id=mp[st[i]];
for(int j=0;j<n;++j)num+=st[i][j];
if(num<totk)
{
for(int j=0;j<n;++j)
if(st[i][j]<k[j])
++st[i][j],buy[id][j]=mp[st[i]],--st[i][j];
}
if(num>0)
{
for(int j=0;j<n;++j)
if(st[i][j]>0)
--st[i][j],sell[id][j]=mp[st[i]],++st[i][j];
}
}
}
inline void upd(db v,int dy,int s,int _s,int o)
{
if(f[dy+1][_s]>=v)return;
f[dy+1][_s]=v;
pre[dy+1][_s]=s;
opt[dy+1][_s]=o;
}
inline void dp()
{
for(int i=0;i<=m;++i)
for(int j=0;j<st.size();++j)
f[i][j]=-1.0;
f[0][0]=c;
for(int i=0;i<m;++i)
for(int j=0;j<st.size();++j)
{
int id=mp[st[j]];
if(f[i][id]<0)continue;
upd(f[i][id],i,id,id,0);
for(int k=0;k<n;++k)
{
db cst=s[k]*t[k][i];
if(buy[id][k]!=-1&&f[i][id]>=cst)upd(f[i][id]-cst,i,id,buy[id][k],k+1);
if(sell[id][k]!=-1)upd(f[i][id]+cst,i,id,sell[id][k],-k-1);
}
}
printf("%.2lf
",f[m][0]);
}
void print(int dy,int id)
{
if(!dy)return;
print(dy-1,pre[dy][id]);
if(!opt[dy][id])puts("HOLD");
else if(opt[dy][id]>0)printf("BUY %s
",ch[opt[dy][id]-1]);
else printf("SELL %s
",ch[-opt[dy][id]-1]);
}
int main()
{
while(scanf("%lf%d%d%d",&c,&m,&n,&totk)==4)
{
for(int i=0;i<n;++i)
{
scanf("%s%d%d",ch[i],&s[i],&k[i]);
for(int j=0;j<m;++j)scanf("%lf",&t[i][j]);
}
mp.clear(),st.clear();vector<int>v;
predfs(0,0,v);_init();
dp();print(m,0);
}
return 0;
}
description:
求长度为n的01串个数,满足其中不含长度长度大于等于k的回文串
data range:
(Nle 400)
(kle 10)
solution:
容易发现如果存在长度大于等于k的回文子串,那么其中必然存在长度为k或k+1的回文子串
观察到k很小,于是我们考虑状态压缩
记(f_{i,s})表示现在在第i位最后k位形成的01串是s,考虑到最后一位的方案数
那么只要考虑第i+1位填0或1同时判断此时是否合法就可以进行转移了
边界就是到最后就返回1
#include<bits/stdc++.h>
using namespace std;
const int N=405,NN=(1<<11)+5,mod=1e9+7;
int n,k,M;
int f[N][NN];
bool ck(int x,int ws)
{
for(int l=0,r=ws-1;l<=r;++l,--r)
if(((x>>l)&1)!=((x>>r)&1))return false;
return true;
}
inline int add(int x,int y){return x+y>=mod?x+y-mod:x+y;}
int solve(int pos,int s)
{
if(pos==n)return 1;
int &d=f[pos][s];
if(d>=0)return d;d=0;
int w=s&(1<<(k-1)),ns=s-w;
if(!ck(s<<1,k+1)&&!ck(ns<<1,k))d=add(d,solve(pos+1,ns<<1));
if(!ck(s<<1|1,k+1)&&!ck(ns<<1|1,k))d=add(d,solve(pos+1,ns<<1|1));
return d;
}
int main()
{
int t;scanf("%d",&t);
while(t--)
{
scanf("%d%d",&n,&k);
if(n<k)
{
int ans=1;
while(n--)ans=add(ans,ans);
printf("%d
",ans);
continue;
}
M=1<<k;int ans=0;
memset(f,-1,sizeof(f));
for(int i=0;i<M;++i)
if(!ck(i,k))ans=add(ans,solve(k,i));
printf("%d
",ans);
}
return 0;
}
description:
给出一个N*M的网格图并给定起点和K个特殊点,求一条从起点出发后又回到起点的尽量短的路径使得它经过每个特殊点一次且仅一次
p.s.每次可以向相邻的八个方向走
data range:
(N,Mle 20)
(Kle 15)
solution:
首先把所有特殊点和起点全部拿出来建成一个图,这样就可以去掉原图的冗余节点
然后可以发现起点和特殊点本质是等价的,即从那个点出发并不影响答案
那么这就是一个经典问题了,直接上状压dp
设(f_{i,s})表示当前在第i个点,还需访问s中的节点各一次后返回0节点所需要走的最短长度
那么就有状态转移方程:(f_{i,s}=min(f_{i,s-{j}}+dis(i,j)))其中(jin s)
边界就是当s为空集时返回(dis(0,i))
time space complexity:
时间:(O(n^2*2^n))
空间:(O(n*2^n))
code:
#include<bits/stdc++.h>
#define pii pair<int,int>
#define fi first
#define se second
using namespace std;
const int N=23,M=16,MAXN=(1<<M)+5,inf=1e9;
int n,m;
char ch[N][N];
vector<pii>nut;
inline int dis(pii x,pii y){return max(abs(x.fi-y.fi),abs(x.se-y.se));}
int f[M][MAXN];
int solve(int pos,int s)
{
if(!s)return dis(nut[0],nut[pos]);
int &d=f[pos][s];
if(d>=0)return d;d=inf;
for(int i=0;i<nut.size();++i)
if(i!=pos&&(1<<i)&s)
d=min(d,solve(i,s^(1<<i))+dis(nut[pos],nut[i]));
return d;
}
int main()
{
while(scanf("%d%d",&n,&m)==2)
{
memset(f,-1,sizeof(f));
nut.clear();
for(int i=1;i<=n;++i)
{
scanf("%s",ch[i]+1);
for(int j=1;j<=m;++j)
if(ch[i][j]!='.')nut.push_back(make_pair(i,j));
}
if(nut.size()==1){puts("0");continue;}
int cnt=nut.size();
printf("%d
",solve(0,(1<<cnt)-1));
}
return 0;
}
description:
给你一个有n+1个点的有向完全图,用矩阵的形式给出任意两个不同点之间的距离。现在要你求出从0号点出发,走过1到n号点至少一次,然后再回到0号点所走的最少距离。
data range:
(Nle 10)
solution:
这道题第一眼看上去跟上一道题一模一样
然后直接打上去,结果样例都没过。。。
仔细看了看,原来这道题的图是有向的并且可以多次经过同一个节点
于是我们要记(f_{u,s})表示当前在u点,已经走过的点的集合为s,遍历所有点后回到0节点要走的最短距离
那么有(f_{u,s}=min(dis(u,v)+f_{v,scup v}))
边界条件就是走完所有点后返回(dis(u,0))
time space complexity:
时间:(O(n^2*2^n))
空间:(O(n*2^n))
code:
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=15,MAXN=2500,inf=1e9;
int n,G[N][N],f[N][MAXN],st;
int solve(int u,int s)
{
if(s==st-1)return G[u][0];
int &d=f[u][s];
if(d>=0)return d;d=inf;
for(int v=0;v<=n;++v)
if(v!=u)d=min(d,G[u][v]+solve(v,s|(1<<v)));
return d;
}
int main()
{
while(scanf("%d",&n)==1&&n)
{
for(int i=0;i<=n;++i)
for(int j=0;j<=n;++j)
scanf("%d",&G[i][j]);
st=(1<<(n+1));
memset(f,-1,sizeof(f));
printf("%d
",solve(0,0));
}
return 0;
}
description:
给出一个N*M的网格图,有些地方可以放炮塔有些地方不能。要求放置尽量多的炮塔,使得没有任意一个炮塔在另一个炮塔的攻击范围内。
一个炮塔的攻击范围如下:
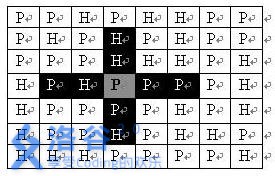
data range:
(Nle 100) (Mle 10)
solution:
这道题如果用我自己的老套路似乎不是很好做(就是不预处理,每一层都现填)
但是如果考虑先提前预处理出同一行内不冲突的所有状态(其实很少)
再在此状态上进行dp,就比较容易了
记(f_{i,s0,s1})表示在第i行状态为s0,第i-1行状态为s2时对应的最小答案
那么就有(f_{i,s0,s1}=max(f_{i-1,s1,s2}+bitcount(s0)))其中s0,s1,s2要互相都不冲突并且也不能和地图冲突
答案不断取最大值就可以了
code:
#include<bits/stdc++.h>
using namespace std;
const int N=105,M=11,MAXN=560;
int n,m,a[N];
int f[N][MAXN][MAXN],num[MAXN];
vector<int>z;
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;++i)
{
char ch[M];scanf("%s",ch);
for(int j=0;j<m;++j)
a[i]<<=1,a[i]|=(ch[j]=='H');
}
int st=1<<m;
for(int i=0;i<st;++i)
{
if((i&(i>>1))||(i&(i>>2)))continue;
num[z.size()]=__builtin_popcount(i);z.push_back(i);
}
int ans=0;
for(int i=1;i<=n;++i)
for(int j=0;j<z.size();++j)
{
if(z[j]&a[i])continue;
for(int k=0;k<z.size();++k)
{
if((z[k]&z[j])||(z[k]&a[i-1]))continue;
for(int k2=0;k2<z.size();++k2)
{
int s=z[j],s1=z[k],s2=z[k2];
int &d=f[i][j][k];
if((s2&s1)||(s2&s)||(i>1&&(s2&a[i-2])))continue;
d=max(d,num[j]+f[i-1][k][k2]);
ans=max(ans,d);
}
}
}
printf("%d
",ans);
return 0;
}
description:
有N头牛在大小为2*B的举行中,不同牛在不同的位置。问用k个矩形将所有的牛都框起来所需要占的最小面积
data range:
(Nle 1000) (Ble 1.5*10^7)
solution:
这道题开始做的时候都把我搞蒙了。。。
这道dp题比较神,详情请参见代码注释
code:
#include<bits/stdc++.h>
using namespace std;
const int N=1005;
int t,n,k,b;
int x[N],y[N],_y[N],f[N][N][5];//f[i][j][k]表示在第i列(离散化后的)已经用了j个矩形,当前状态为k所需要的最小占地面积
/*
1->覆盖第一行
2->覆盖第二行
3->覆盖两行,为同一个矩形
4->覆盖两行,为不同的矩形
*/
bool a[3][N];
inline void _min(int &x,int y){x=min(x,y);}
int main()
{
scanf("%d",&t);
while(t--)
{
scanf("%d%d%d",&n,&k,&b);
for(int i=1;i<=n;++i)
{
scanf("%d%d",&x[i],&y[i]);
_y[i]=y[i];
}
//离散化
sort(_y+1,_y+n+1);
int tot=unique(_y+1,_y+n+1)-_y-1;
for(int i=1;i<=n;++i)
y[i]=lower_bound(_y+1,_y+tot+1,y[i])-_y;
memset(a,0,sizeof(a));
for(int i=1;i<=n;++i)a[x[i]][y[i]]=1;
//初始化
memset(f,0x3f,sizeof(f));
f[0][0][0]=0;
//采用刷表法
for(int i=0;i<tot;++i)
for(int j=0;j<=k;++j)
for(int tp=0;tp<5;++tp)
{
const int &d=f[i][j][tp];//cout<<d<<endl;
//考虑全部都新开一个矩形的情况
if(!a[1][i+1])_min(f[i+1][j+1][2],d+1);
if(!a[2][i+1])_min(f[i+1][j+1][1],d+1);
_min(f[i+1][j+1][3],d+2);
_min(f[i+1][j+2][4],d+2);
//考虑不添加的情况
int len=_y[i+1]-_y[i];
if(tp==1)!a[2][i+1]?_min(f[i+1][j][tp],d+len):_min(f[i+1][j+1][4],d+len+1);
//直接延续过来or上一个延续过来同时下面重新开一个
else if(tp==2)!a[1][i+1]?_min(f[i+1][j][tp],d+len):_min(f[i+1][j+1][4],d+len+1);
else if(tp==3)_min(f[i+1][j][tp],d+len*2);//直接向后面延续
else if(tp==4)
{
_min(f[i+1][j][tp],d+len*2);//上下都继续延续
!a[2][i+1]?_min(f[i+1][j][1],d+len):_min(f[i+1][j+1][4],d+len+1);
//下面没有?将下面的矩形收尾:上面继续延续下面重新开
!a[1][i+1]?_min(f[i+1][j][2],d+len):_min(f[i+1][j+1][4],d+len+1);
}
}
int ans=min(f[tot][k][1],min(f[tot][k][2],min(f[tot][k][3],f[tot][k][4])));
printf("%d
",ans);
}
return 0;
}
description:
有一个N行M列的网格图,有些地方不能种草。求有多少种种草方案满足没有任意两块草是相邻的
data range:
(N,Mle 12)
solution:
可以看作是炮兵阵地的严格弱化版
dp时当前行的状态只受上一行的影响
记(f_{i,s})表示在第i行且当前状态为s的总方案数
那么(f_{i,s}=f_{i+1,ns})其中ns是满足第i+1行的条件且不与s冲突的
边界就是到最后返回1
code:
#include<cstdio>
#include<cstring>
#include<vector>
using namespace std;
const int N=13,MAXN=(1<<N)+5,mod=1e8;
vector<int>g;
int n,m,a[N];
int f[N][MAXN];
int solve(int pos,int s0)
{
if(pos==n+1)return 1;
int &d=f[pos][s0];
if(d>=0)return d;d=0;
for(int i=0;i<g.size();++i)
if((g[i]&a[pos])==g[i]&&!(g[i]&s0))
d=(d+solve(pos+1,g[i]))%mod;
return d;
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;++i)
for(int j=1;j<=m;++j)
{
int x;scanf("%d",&x);
a[i]<<=1,a[i]|=x;
}
int M=1<<m;
for(int i=0;i<M;++i)
if(!(i&(i<<1)))g.push_back(i);
memset(f,-1,sizeof(f));
printf("%d",solve(1,0));
return 0;
}
description:
要以不同方式将宽为2高为1的小长方形填充到一个高h×宽w的长方形中,可以有多少种方式?
data range:
(1≤h,w≤11)
soluiton:
跟前面的两道题差不多,都是类似地状态定义然后转移
不过这题我是用的旧方法,每一层都是重新填一遍
似乎预处理会使得代码更加清楚一些
code:
#include<cstdio>
#include<cstring>
using namespace std;
typedef long long ll;
const int N=12,MAXN=(1<<N)+5;
int h,w;
ll f[N][MAXN];
ll solve(int pos,int d,int s0,int s)
{
if(d>=w)return solve(pos+1,0,s,0);
if(pos==h+1)return !s0;
if(s0&(1<<d))return solve(pos,d+1,s0,s);
ll &o=f[pos][s0],ans=0;if(!d&&o>=0)return o;
ans=solve(pos,d+1,s0,s|(1<<d));
if(d<w-1&&!(s0&(1<<(d+1))))ans+=solve(pos,d+2,s0,s);
if(!d)o=ans;
return ans;
}
int main()
{
while(scanf("%d%d",&h,&w)&&h&&w)
{
if((h*w)&1){puts("0");continue;}
memset(f,-1,sizeof(f));
printf("%lld
",solve(1,0,0,0));
}
return 0;
}
description:
可以用多少种方式用2x1多米诺骨牌平铺3xn矩形?
data range:
(0le nle 30)
solution:
直接套用上一道题的做法即可
p.s.不过好像有一种神仙的直接递推的做法
code:
#include<cstdio>
#include<cstring>
using namespace std;
const int N=30,MAXN=20;
int h,w;
int f[N][MAXN];
int solve(int pos,int d,int s0,int s)
{
if(d>=w)return solve(pos+1,0,s,0);
if(pos==h+1)return !s0;
if(s0&(1<<d))return solve(pos,d+1,s0,s);
int &o=f[pos][s0],ans=0;if(!d&&o>=0)return o;
ans=solve(pos,d+1,s0,s|(1<<d));
if(d<w-1&&!(s0&(1<<(d+1))))ans+=solve(pos,d+2,s0,s);
if(!d)o=ans;
return ans;
}
int main()
{
while(scanf("%d",&h))
{
if(h==-1)break;w=3;
if((h*w)&1){puts("0");continue;}
memset(f,-1,sizeof(f));
printf("%d
",solve(1,0,0,0));
}
return 0;
}