分类数据
分类数据是对事物进行分类的结果,它虽然是用数值表示,但是数值仅仅反映对象的不同特征,其大小没有意义。分类数据的结果是频数,对其进行统计分析主要利用$chi^2$分布。
$chi^2$统计量
$chi^2$统计量可用于测定2个分类变量之间的相关程度。用$f_o$表示观察值频数,$f_e$表示期望值频数,则
$$chi^2=sum frac{(f_o-f_e)^2}{f_e}$$
利用$chi^2$统计量,可以对分类数据进行拟合优度检验和独立性检验。
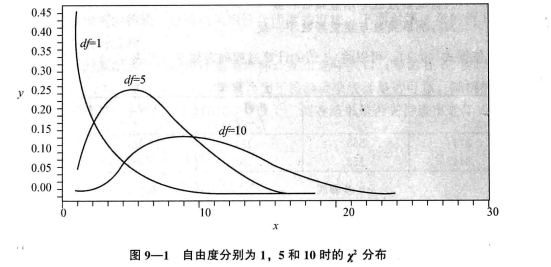
拟合优度检验
拟合优度检验(goodness of fit test):
依据总体分布,计算出各类别的期望频数,与观察频数进行对比,判断两者是否有显著差异,从而对分类变量进行分析。
原假设和备择假设
$H_0$:观察频数与期望频数一致
$H_1$:观察频数与期望频数不一致
检验统计量
$$chi^2=sum frac{(f_o-f_e)^2}{f_e}$$
自由度为$df=R-1$,R为分类变量的类型的个数。
在假设检验中,我们在二项分布总体、大样本情况下,对总体比例采用z检验:
$$z=frac{p-pi_0}{sqrt{frac{pi_0(1-pi_0)}{n}}}$$
对于总体比例,同样可以使用拟合优度检验(比例可视为2个类别的分类变量)。z检验只能针对二项分布问题,而$chi^2$检验既可以分析二项分布,也可以分析多项分布(对总体的多个比例的假设进行检验)。
列联分析:独立性检验
拟合优度检验是针对一个分类变量的检验,对于两个分类变量,我们会关心它们是否有关联,称为独立性检验,通过列联表的方式呈现。
列联表
列联表是由2个以上的变量交叉分类的频数分布表。将行变量视为R(3类),列变量视为C(3类),可以把每一个列联表称为R×C列联表。下表为3×3列联表:

独立性检验
分析列联表中行变量和列变量是否独立。
原假设和备择假设
$H_0$:不存在依赖关系
$H_1$:存在依赖关系
计算个单元期望频数值
$$f_e=frac{RT}{n} imes frac{CT}{n} imes n=frac{RT imes CT}{n}$$
其中$f_e$是给定单元中的期望频数,$RT$是单元所在行的合计,$CT$是单元所在列的合计,$n$是样本量。
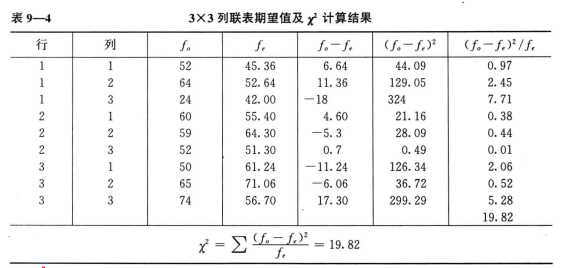
自由度为$df=(R-1)(C-1)$。
由于$chi^2>chi^2_{0.05}(4)=9.488$,故拒绝$H_0$,接受$H_1$,地区与等级之间存在依赖关系。
列联表中的相关性测量:品质数据的相关系数
$chi^2$分布可以检验两个分类变量的独立性,如果它们不独立,则相关程度有多大?相关系数表示两个变量之间的相关程度,列联表中的变量是分类变量,它们之间的相关叫做品质相关。常用的品质相关系数有$varphi $系数、$c$系数、$V$系数。
$varphi $相关系数
描述2×2列联表数据相关程度,计算公式为
$$varphi =sqrt{frac{chi^2}{n}}$$

每个单元的期望频数为:
$$e_{11}=frac{(a+b)(a+c)}{n}$$
$$e_{21}=frac{(a+c)(c+d)}{n}$$
$$e_{12}=frac{(a+b)(b+d)}{n}$$
$$e_{22}=frac{(b+d)(c+d)}{n}$$
$chi^2$值为:
$$chi^2=frac{a-e_{11}}{e_{11}}+frac{b-e_{12}}{e_{12}}+frac{c-e_{21}}{e_{21}}+frac{d-e_{22}}{e_{22}}=frac{n(ad-bc)^2}{(a+b)(c+d)(a+c)(b+d)}$$
则
$$varphi =sqrt{frac{chi^2}{n}}=frac{ad-bc}{sqrt{(a+b)(c+d)(a+c)(b+d)}}$$
当ad=bc时,$varphi$=0,2个变量独立;
当b=0,c=0时,$varphi$=1,2个变量完全相关;
当a=0,d=0时,$varphi$=-1,2个变量完全相关;
因此,对于2×2列联表,$varphi $系数的取值在0~1之间,绝对值越大,相关程度越高。
对于R或C大于2的列联表,$varphi $值无上限。
列联相关系数
又称c系数,主要用于大于2×2列联表的情况,计算公式为:
$$c=sqrt{frac{chi^2}{chi^2+n}}$$
当2个变量相互独立时,c=0;其最大值小于1,且随着R和C的增大而增大。它对总体的分布没有任何要求,但只有2个列联表的行数列数一致时,用c系数进行比较才有意义。
V相关系数
$$V=sqrt{frac{chi^2}{n imes min[(R-1),(C-1)]}}$$
当两个变量相互独立时,V=0;
当两个变量完全相关时,V=1。
列联分析中应注意的问题
条件百分表的方向
一般把$X$(自变量)作为列向量,把$Y$(因变量)作为行向量,便于更好地表现原因对于结果的影响。
$chi^2$分布的期望值准则
用$chi^2$分布进行独立性检验,要求样本量必须足够大。关于每个单元的频数,有2条准则:
1. 如果只有2个单元,则每个单元的期望频数$f_e$必须大于或等于5;
2. 如果有2个以上单元,则要求20%的单元期望频数$f_e$大于或等于5。
期望频数$f_e$过小,$frac{(f_o-f_e)^2}{f_e}$会不适当地增大,造成对$chi^2$的高估,导致不适当地拒绝$H_0$。将较小的$f_e$合并,可得到合理的结论。