0-1背包问题入门

        最近在做背包问题，今天写点东西总结一下。

        背包问题，常见的有三种类型：基本的0-1背包、完全背包和多重背包、二维背包 

        首先是基本的0-1背包问题。因为这里的物品一般指花瓶、玉器什么的，要么拿、要么不拿，只有0和1两种状态，所以也叫0-1背包。0-1背包虽然简单，却很重要，是“万法之源”，是其他几类问题的基础。 

        初学者有时会认为，0-1背包可以这样求解：计算每个物品的Vi/Wi，然后依据Vi/Wi的值，对所有的物品从大到小进行排序。其实这种贪心方法是错误的。如下表，有三件物品，背包的最大负重量是50，求可以取得的最大价值。 

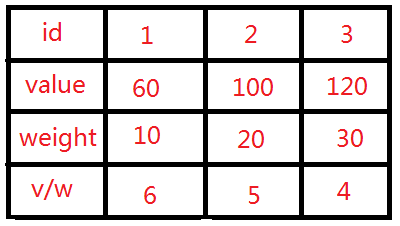
        其实，0-1背包是DP的一个经典实例，可以用动态规划求解。

DP求解过程可以这样理解：对于前i件物品，背包剩余容量为j时，所取得的最大价值（此时称为状态3）只依赖于两个状态。

状态1：前i-1件物品，背包剩余容量为j。在该状态下，只要不选第i个物品，就可以转换到状态3。

状态2：前i-1件物品，背包剩余容量为j-w[i]。在该状态下，选第i个物品，也可以转换到状态3。

因为，这里要求最大价值，所以只要从状态1和状态2中选择最大价值较大的一个即可。 

状态转换方程：

dp( i,j ) = Max( dp( i-1, j ), dp( i-1, j-w[i] ) + v[i] )

dp( i,j )表示前i件物品，背包剩余容量为j时，所取得的最大价值。 

        还是结合上面的例子来说明吧。有三件物品，背包的最大负重量是50，求可以取得的最大价值。下图表示了DP自上而下的求解过程。

编程实现：

       一般来说，有了状态方程，直接编程实现就game over。dp( i,j )，用一个二维数组来实现，然后用一个两层循环就可以了。不过，有时选择的物品很多，背包的容量很大，这时要用二维数组往往是不现实的。这里有一个方法，可以进行空间压缩，然后使用一维数组实现。

       还是结合上面的例子，有三件物品，背包的最大负重量是5，求可以取得的最大价值。为了方面说明，物品weight依次为：1，2，3。二维数组下的求解顺序，物品数1--->n, 背包容量1--->w。如图，要使用一维数组，背包容量要采用倒序，即w--->1, 只有这样对于方程dp( j ) = Max( dp( j ), dp (j-w[i] ) + v[i] )，才能达到等式左边才表示i,而等式右边表示i-1的效果。POJ对于题目：3624。下面附代码。

 

        完全背包和多重背包。有了基本的0-1背包基础，下面的东西也就好理解了。 完全背包，指每个物品有无限多个。 多重背包，指每个物品的数量是有限的。当然，这时的问题不再是拿与不拿，而是拿多少的问题，当然不能超过背包容量。 

状态转换方程：

dp( i,j ) = Max( dp( i-1, j ), dp( i-1, j-k*w[i]) + k*v[i] ) ( 0 <= k <= c/ w[i] )

编码实现：

如果直接编码，用三层循环，往往会超时。这样有一种很有效的压缩方式：二进制压缩。把原来的物品按照2的n次方进行重新组合。用1、2、4、8…进行组合，可以组合出任意的数字。POJ题目：1276

POJ3624

 

#include <iostream>
using namespace std;

//***********************常量定义*****************************

const int MAX_NUM = 3500;
const int MAX_WEIGHT = 14000;

//*********************自定义数据结构*************************



//********************题目描述中的变量************************

int weight[MAX_NUM];
int value[MAX_NUM];


//**********************算法中的变量**************************

//进行空间压缩，使用一维数组
int dp[MAX_WEIGHT];


//***********************算法实现*****************************

void Solve( int n, int w )
{    
    for( int i=1; i<=n; i++ )
    {
        //因为使用了一维数组，所有j要按照递减顺序
        for( int j=w; j>=weight[i]; j-- )
        {            
            if( dp[j-weight[i]] + value[i] > dp[j] )
                dp[j] = dp[j-weight[i]] + value[i];            
        }
    }
    cout << dp[w] << endl;
}


//************************main函数****************************

int main()
{
    //freopen( "in.txt", "r", stdin );    

    int n, w;
    cin >> n >> w;        

    for( int i=1; i<=n; i++ )
    {
        cin >> weight[i] >> value[i];
    }
    Solve( n, w );
    
    return 0;
}

POJ1276

#include <iostream>
using namespace std;

//***********************常量定义*****************************

const int MAX_NUM = 1005;
const int MAX_CASH_REQUEST = 100005;


//*********************自定义数据结构*************************




//********************题目描述中的变量************************

int cashRequest;
int cashKind;


//**********************算法中的变量**************************
//dp[i][j]表示前i个物件，cashRequest == j时，所能获得的最大金额
int dp[MAX_CASH_REQUEST];
//使用二进制压缩，形成的新物件
int cnt;
int value[MAX_NUM];


//***********************算法实现*****************************

void Solve()
{
    //采用0-1背包求解
    for( int i=1; i<=cnt; i++ )
    {        
        for( int j=cashRequest; j>=value[i]; j-- )
        {
            dp[j] = dp[j] > dp[j-value[i]] + value[i] ? dp[j] : dp[j-value[i]] + value[i];
        }                
    }
    cout << dp[cashRequest] << endl;
}


//************************main函数****************************

int main()
{
    //freopen( "in.txt", "r", stdin );
    
    while( cin >> cashRequest >> cashKind )
    {
        //输入
        for( int i=1; i<=cashKind; i++ )
        {
            int num, deno;
            cin >> num >> deno;
            
            //二进制压缩
            for( int j=1; j<=num; j*=2 )
            {
                value[++cnt] = deno * j;
                num -= j;
            }                
            if( num > 0 )    value[++cnt] = num * deno;            
        }

        //处理
        Solve();
        
        //清空全局变量
        cnt = 0;
        memset( value, 0, sizeof(value) );
        memset( dp, 0, sizeof(dp) );
    }    

    return 0;
}