个人项目作业
| 项目 | 内容 |
|---|---|
| 作业所属课程 | 2020春季计算机学院软件工程(罗杰,任健) |
| 作业要求 | 个人项目作业 |
| 教学班级 | 005 |
| 项目地址 | 个人项目地址 |
PSP表格
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | ||
| · Estimate | · 估计这个任务需要多少时间 | 15 | 10 |
| Development | 开发 | ||
| · Analysis | · 需求分析 (包括学习新技术) | 60 | 120 |
| · Design Spec | · 生成设计文档 | 15 | 20 |
| · Design Review | · 设计复审 (和同事审核设计文档) | 5 | 5 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 10 | 5 |
| · Design | · 具体设计 | 20 | 20 |
| · Coding | · 具体编码 | 90 | 100 |
| · Code Review | · 代码复审 | 15 | 30 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 30 | 120 |
| Reporting | 报告 | ||
| · Test Report | · 测试报告 | 15 | 10 |
| · Size Measurement | · 计算工作量 | 15 | 15 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 20 | 20 |
| 合计 | 310 | 475 |
解题思路
对于给定的N条直线,询问平面中有多少点在至少2条给定的直线上,即求出N条直线有多少不重复的交点。
首先我分析到输入部分,每条直线对应线上不同的两点,我首先根据这两点计算得到直线的标准方程式,记得到三个重要参数:a, b, c:
$$
ax + by + c = 0, a = y2 - y1, b = x1 - x2, c = y1x2 - x1y2;
$$
同时我们保证a始终大于0。
得到每个直线的标准方程式后,我们就可以进行两两比较得到交点数了,若两条直线的斜率不等,则说明两条直线有交点,同时记录交点的坐标信息:
$$
x = (b1c2 - c1b2)/(a1b2 - a2b1), y = (a2c1 - a1c2)/(a1b2 - a2b1);
$$
在比对所有直线的相交情况后,我们就可以去掉计数了重复的点了,最后得到就是所有直线不重复的交点,即平面中至少在2条给点直线上的点数。
设计实现
程序中有四个函数,设计了两个结构体:
直线标准式信息(LINE):
记录了每条直线的a, b, c相应的值,采用double数据类型。
交点坐标信息(Point2d):
记录每个交点的坐标轴信息,包括x, y,采用double数据类型。
主函数(main):
主要用于命令行的输入输出,首先对命令行进行处理得到所要的数据,将每个直线的两点坐标信息读取传递给调用函数,返回得到直线标准方程式信息,然后调用计算交点数函数得到无重复的交点个数,返回到输出文件中。
直线标准方程式函数(makeline):
根据所给的直线两点坐标,计算得到直线标准式a, b, c值,其中保证a值大于0,,返回一个LINE数据结构体。
计算交点函数(calculateCrossPointsNum):
遍历每条直线,查看两两直线是否相交,统计并记录交点坐标信息,然后遍历交点信息,取出重复的交点。
判断直线是否相交函数(lineintersect):
通过比较所给两条直线的斜率,分析两条直线是否平行,若直线相交计算并记录交点的坐标信息。
函数之间的关系:
主函数main通过调用makeline来根据点的坐标信息得到直线的标准式信息,然后通过calculateCrossPointsNum计算得到交点个数,calculateCrossPointsNum函数调用lineintersect来判断两两直线是否相交:

单元测试主要根据样例分析多种不同情况,考虑一条直线,多条直线相交一点,多条平行线等问题,均可实现。

性能分析表
性能分析图(由 VS 2019 的性能分析工具自动生成) :
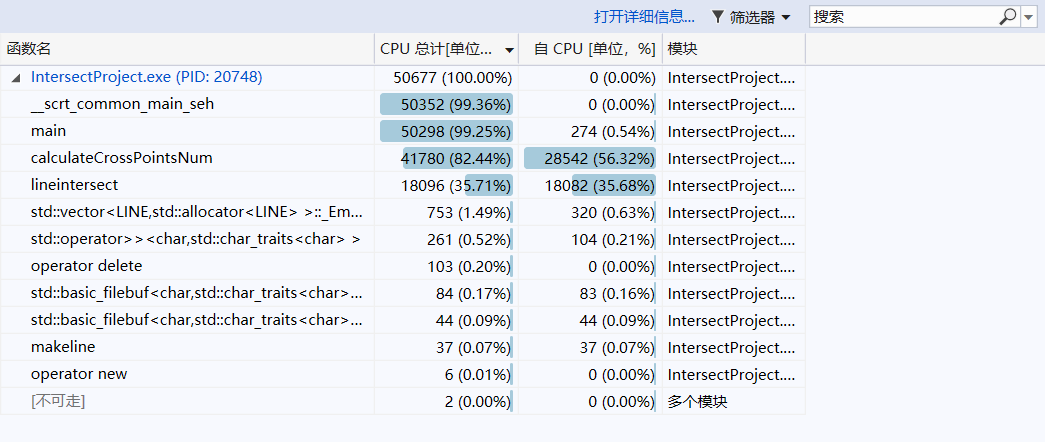

程序中消耗最大的是比较斜率过程。
代码说明
通过命令行输入直线数据:
int main(int argc, char* argv[])
{
ifstream in;
ofstream out;
for (int i = 0; i < argc; i++) {
if ((string)argv[i] == "-i") {
in.open(argv[i + 1]);
}
else if ((string)argv[i] == "-o") {
out.open(argv[i + 1]);
}
}
int N; // 直线个数
in >> N;
根据已知两点坐标,求过这两点的直线解析方程:a*x + b * y + c = 0:
LINE makeline(double x1,double y1,double x2,double y2)
{
LINE tl;
int sign = 1;
tl.a = y2 - y1;
if (tl.a < 0) {
sign = -1;
tl.a = sign * tl.a;
}
tl.b = sign * (x1 - x2);
tl.c = sign * (y1 * x2 - x1 * y2);
return tl;
}
如果两条直线 l1(a1x+b1y+c1 = 0), l2(a2x+b2y+c2 = 0)相交,返回true,且返回交点p:
bool lineintersect(LINE l1, LINE l2, Point2d &p)
{
double d = l1.a * l2.b - l2.a * l1.b;
if (abs(d) < EP)
{
return false;
}
p.x = (l2.c * l1.b - l1.c * l2.b) / d;
p.y = (l2.a * l1.c - l1.a * l2.c) / d;
return true;
}
去掉重复点:
for (int i = 0; i < pnts.size() - 1; i++)
{
for (int j = i + 1; j < pnts.size(); j++)
{
if (pnts[i].x == pnts[j].x && pnts[i].y == pnts[j].y)
{
pnts.erase(pnts.begin() + j);
j--;
}
}
}
Code Quality Analysis分析
