马尔科夫:
一、马尔科夫链定义
是一种随机时间序列,它未来取值只与现在有关,而与过去无关,即:无后效性,系统在每一时刻的状态仅仅取决于前一时刻的状态,具备这一特性的离散型随机过程被称为马尔可夫链。
二、马尔科夫链特点
1.无后效性;
2.离散性。
3.马尔科夫的特性
a.
其中后面的n表示转移的步骤数。0+n=n.
b.极限概率分布,长期稳定状态时:
c.期望利润(一步转移)

时间序列模型:
(1)移动平均法
a.简单移动平均:
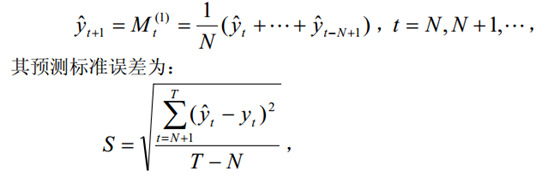
2..加权移动平均

3.趋势移动平均



(2)指数平滑法
一次移动平均实际上认为最近 N 期数据对未来值影响相同,都加权1/N;而 N 期以前的数据对未来值没有影响,加权为 0。但是,二次及更高次移动平均数的权数却不是1/N,且次数越高,权数的结构越复杂,但永远保持对称的权数,即两端项权数小,中间项权数大,不符合一般系统的动态性。一般说来历史数据对未来值的影响是随时间间隔的增长而递减的。所以,更切合实际的方法应是对各期观测值依时间顺序进行加权平均作为预测值。
a.一次指数平滑法

b.二次指数平滑法
一次指数平滑法虽然克服了移动平均法的缺点。但当时间序列的变动出现直线趋
势时,用一次指数平滑法进行预测,仍存在明显的滞后偏差。

(3)自适应滤波法
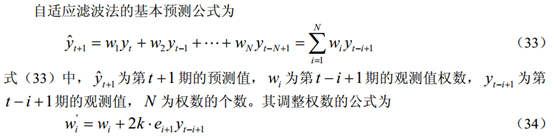
(4)趋势外推预测法
a.指数曲线法


b.修正指数曲线法
利用指数曲线外推来进行预测时,存在着预测值随着时间的推移会无限增大的情况。这是不符合客观规律的。因为任何事物的发展都是有一定限度的。例如某种畅销产品,在其占有市场的初期是呈指数曲线增长的,但随着产品销售量的增加,产品总量接近于社会饱和量时。
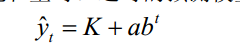


(5)自回归移动平均模型(ARMA)
线性回归分析
线性回归中一些概念:



对于上面公式:SSr----SSE,残差平方和
SSy----SST总离差平方和
SSR----SSE.回归平方和


其中:k为自变量个数,n为观察序列
