神经网络
神经网络优化算法:
- 附加动量法
- 自适应学习速率
- 链式数据重组增加样本
- 增长率指标。各属性增长率。则此时样本集从i+1开始
- 时间窗口时间序列:引入当前所研究的经济指标前后j年的关系。则此时训练样本集从i+j开始。
灰色系统理论:
灰色系统理论将随机量看作是在一定范围内变化的灰色量,按适当的办法
将原始数据进行处理,将灰色数变换为生成数,从生成数进而得到规律性较强的生成函数。
(1)数据变换技术
为保证建模的质量与系统分析的正确结果,
对收集来的原始数据必须进行数据变换
和处理,使其消除量纲和具有可比性。
a.初始值变换
b.均值话变换
c.百分比变换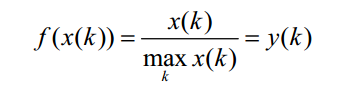
d.倍数变换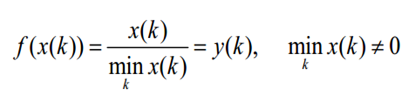
e.归一化变换(X0为大于0的某个值)
f.极差最大化变换
g.区间值化变换
(2)关联分析
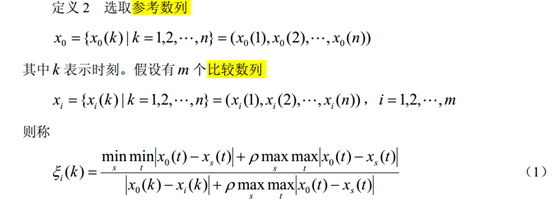

得到结论为:各比较数列对参考数列的影响程度。
当参考数列不唯一时,得到的是一个关联矩阵:相当于将上述的过程重复n遍,其中n为参考数列的个数。
(3)生成数
在研究社会系统、 经济系统等抽象系统时, 往往要遇到随机干扰 (即所谓 “噪声”)。人们对“噪声”污染系统的研究大多基于概率统计方法。但概率统计方法有很多不足之处:要求大量数据、要求有典型的统计规律、计算工作量等。对灰色数的处理不是找概率分布或求统计规律,而是利用数据处理的办法去寻找数据间的规律。通过对数列中的数据进行处理,产生新的数列,以此来挖掘和寻找数的规律性的方法,叫做数的生成。
a.累加生成
一次累加
b.累减生成(对于生成数的还原)

c.均值生成
邻值生成数:
等权邻值生成数: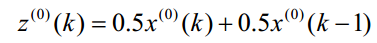
(4)GM(1,1)模型
利用GM(1,1)模型预测的步骤:
a.数据的检验与处理 。保证所有的值落在
。保证所有的值落在 。可以做平移变换,加上一个常数。
。可以做平移变换,加上一个常数。
b.建立模型

并且:
c.检验预测值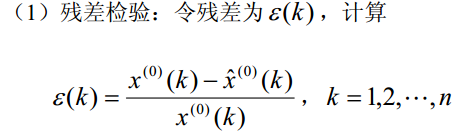 ,
,
若<0.2则认为达到一般要求,<0.1,则认为达到较高的要求。

若<0.2则认为达到一般要求,<0.1,则认为达到较高的要求。
d.关于模型中a,b值得解
建立灰微分方程:


GM(1,1)模型可以表示为矩阵方程Y = Bu
通过最小二乘法解得: